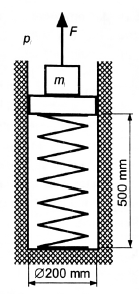
من یک مثال سختر میارم محاسبه ضربه به قاب از یک چرخ فلایویل و سیستم پیستونی من از همین روش برای پرسیدن سوال متفاوتی استفاده می کنم: در سیستم اینرسی فلایویل و پیستون، چگونه نیروهای منتقل شده به قاب پشتیبان محور چرخ فلایویل را محاسبه می کنید؟
شما پیستونی را در یک سیلندر تصور کنید تا پیستون به صورت افقی حرکت کند. سیلندر در دو انتها باز است (بدون فشرده سازی گاز). گرانش، و اینکه سیستم در خلاء ایزوله شده است.
پیستون دارای یک میله اتصال است که به یک فلایویل گردان متصل شده است. در نتیجه پیستون در داخل سیلندر به سمت جلو و عقب نوسان می کند. حرکت پیستون شبیه حرکت هارمونیک ساده است. انرژی جنبشی آن در طول زمان، بین حداکثر در وسط سیلندر، تا صفر در دو انتهای استوانه در نوسان است.
برای حرکت هارمونیک ساده (به عنوان مثال، وزنه ای متصل به فنر، و نوسان افقی روی میز بدون اصطکاک)، به خوبی شناخته شده است که نوسان انرژی جنبشی وزن دقیقاً با یک نوسان همزمان انرژی پتانسیل متعادل می شود (به عنوان مثال، پتانسیل). انرژی ناشی از فشردگی فنر) به گونه ای که انرژی کل همیشه ثابت بمونه
$\begin{align}
& K = E \sin^2(wt) \\
& P = E \cos^2(wt) \\
& K + P = E
\end{align}$
علاوه بر این، چنین حرکتی نامشخص است (به استثنای اصطکاک و غیره...).
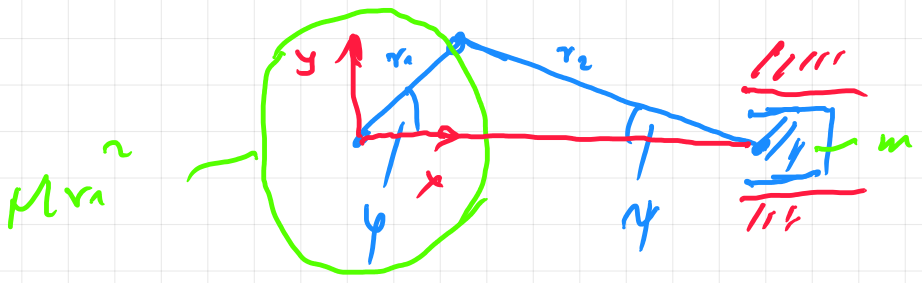
سینماتیک
$\begin{align*}
&x=\cos \left( \varphi \right) r_{{1}}+r_{{2}}\cos \left( \psi
\right)\\
&r_1\,\sin(\varphi)=r_2\,\sin(\psi)
\end{align*}$
از اینجا به دست میارم
$\begin{align*}
&x(\varphi)=\cos \left( \varphi \right) r_{{1}}+r_{{2}}\sqrt {1-{\frac {
\left( \sin \left( \varphi \right) \right) ^{2}{r_{{1}}}^{2}}{{r_
{{2}}}^{2}}}}
\end{align*}$
انرژی جنبشی سنتیک
$\begin{align*}
&T=\frac{m}{2}\left(\frac{\partial x(\varphi)}{\partial\varphi}\,\dot{\varphi}\right)^2+\frac{M\,r_1^2}{2}\,
\dot{\varphi}^2:=\frac{1}{2}\,g(\varphi)\dot{\varphi}^2
\end{align*}$
و با اویلر-لاگرانژ معادله حرکت را بدست اوردم
$\begin{align*}
&\ddot \varphi +\frac 12\,{\frac { \left( {\frac {d}{d\varphi }}g \left(
\varphi \right) \right) {\dot\varphi }^{2}}{g \left( \varphi \right) }
}=0
\end{align*}$
برای بدست آوردن نیروی محدودیت میله $~r_1$، یک شکاف$~q_n~$ را به سمت $~r_1$باز می کنید دیگه بنابراین سینماتیک
$\begin{align*}
&x=\cos \left( \varphi \right) (r_{{1}}+q_n)+r_{{2}}\cos \left( \psi
\right)\\
&(r_1+q_n)\,\sin(\varphi)=r_2\,\sin(\psi)
\end{align*}$
از اینجا من $~x(\varphi~,q_n)$ را بدست اوردم و اکنون دو مختصات تعمیم یافته دارم ,$~\varphi~,q_n$ انرژی جنبشی برابر است با$\begin{align*}
&T=\frac{m}{2}\,v^2+\frac{M\,r_1^2}{2}\,\dot{\varphi}^2\\
&\text{with}\\
&v=\frac{\partial x}{\partial \varphi}\,\dot{\varphi}+
\frac{\partial x}{\partial q_n}\,\dot{q}_n\\\\
\Rightarrow\\
&T:=\frac{1}{2}\,g(\varphi~,q_n)\dot{\varphi}^2+
h(\varphi~,q_n)\,\dot{\varphi}\,\dot{q}_n+\frac{1}{2}\,f(\varphi~,q_n)\,
\dot{q}_n^2
\end{align*}$
اکنون باید از روش اویلر با معادله محدودیت هولونومیک استفاده کنم (من "شکاف را کلوز میکنم") که $q_n=0$ است. من نیروی محدودیت میله λ را محاسبه میکنم
$\begin{align*}
&\lambda=\left(\frac{1}{2}\frac{h(\varphi~,0)\,D_1(g)(\varphi,0)}{g(\varphi,0)}-
\,D_1(h)(\varphi,0)+\frac 12 \frac{\partial}{\partial q_n}\,g(\varphi,q_n)\bigg|_{q_n=0}\right)\,\dot{\varphi}^2\\\
&\text{roham with}\\
&D_1(g)(\varphi,0)=\frac{\partial g}{\partial\varphi}\bigg|_{(\varphi,0)}\qquad
,D_1(h)(\varphi,0)=\frac{\partial h}{\partial\varphi}\bigg|_{(\varphi,0)}\\
\end{align*}$Hesami, sixth
semester of aerospace engineering
رهام حسامی ترم ششم مهندسی هوافضا
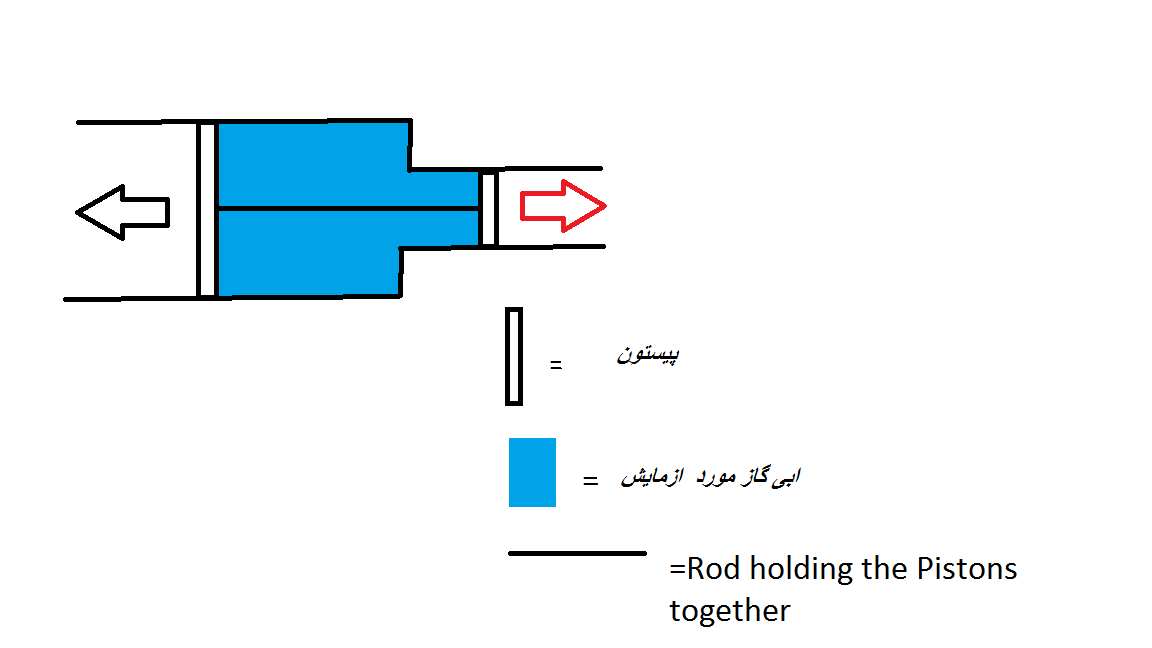
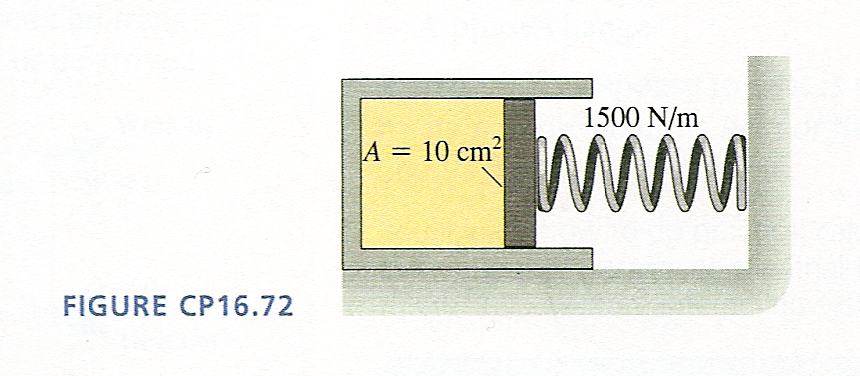دارای یک پیستون متحرکه که به یک فنر متصله. سطح مقطع سیلندر 10 سانتی متر مربع، حاوی 0.0040 مول گاز و ثابت فنر 1500 نیوتن بر متر است. در دمای 20 درجه سانتی گراد فنر نه فشرده میشه و نه کشیده میشه. اگر دمای گاز تا 100 درجه سانتی گراد افزایش یابد فنر چقدر فشرده میشه خوب سه نیرو در هر زمان روی پیستون وارد می شود: pA به سمت راست، patmosA در سمت چپ و kx به سمت راست. هنگامی که سیستم در تعادل است، $pA = p_{\mathrm{atmos}} A + kx$. در $T_1 = 293 \, \mathrm{K}$، رشته نه کشیده و نه فشرده میشه، بنابراین x=0; علاوه بر این، با توجه به اینکه سیستم در حالت تعادله $p_1 A = p_{\mathrm{atmos}} A$ داریم، بنابراین $p_1 = p_{\mathrm{atmos}} = 101.3 \, \mathrm{kPa}$. لذا تغییرناپذیر فوق را می توان اینطور گفت که من نوشتم