$k = A\exp\left(-\frac{E_\mathrm a}{RT}\right),$
همانطور که در نمودار زیر نشان داده شده است، انرژی فعال سازی $E_\mathrm a$ به عنوان نشان دهنده تفاوت در انرژی واکنش دهنده ها و حداقل انرژی مورد نیاز برای تشکیل کمپلکس فعال شده یا حالت گذار است.
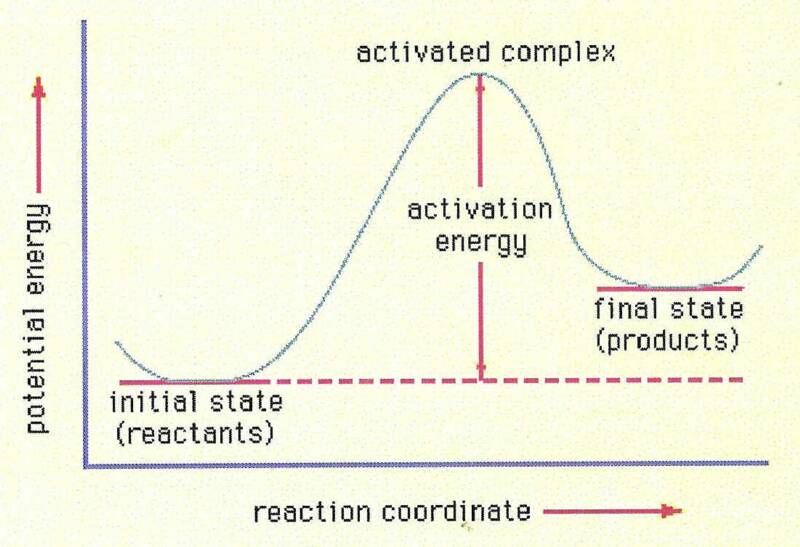
اما این باید اشتباه باشد! همانطور که Ea خود حداقل انرژی است که مولکول ها برای رسیدن به کمپلکس فعال شده باید داشته باشند. یعنی این تفاوت نیست بلکه خود حداقل سطح انرژی است. این تنها راهی است که در آن ثابت می ماند یعنی مستقل از دما (در غیر این صورت با افزایش T، $E_\mathrm a$ پایین می آید) و می تواند در معادله آرنیوس استفاده شود که در آن عبارت نمایی نشان دهنده کسری از مولکول هایی است که انرژی بالاتر یا مساوی دارند. به Ea با توجه به توزیع ماکسول-بولتزمن. گاهی اوقات، انرژی آستانه (Et) به عنوان حداقل انرژی مورد نیاز برای ادامه واکنش و $E_\mathrm a = E_\mathrm t-\mathrm{KE_{average}}$ تعریف می شود. اگر این تعریف درست باشد، انرژی آستانه و نه انرژی فعال سازی باید در معادله آرنیوس باشد. بنابراین باید تعریف واقعی انرژی فعالسازی Ea را توضیح دهم.
حق با من هست که انرژی حالت اولیه تابعی از دما است. اما در عمل برای این معادله، اختلاف انرژی Ea معمولاً برای یک دمای دلخواه (در وسط دیاپازون اندازهگیریهای تجربی) ثابت است و مستقل از دما فرض میشود.
در حالی که این معادله نشان میدهد که انرژی فعالسازی به دما وابسته است، در رژیمهایی که معادله آرنیوس معتبر است، با وابستگی به دما k لغو میشود. بنابراین، Ea را می توان از ضریب سرعت واکنش در هر دمایی (در حد اعتبار معادله آرنیوس) ارزیابی کرد.
در مورد معنای فیزیکی انرژی فعال سازی،هم انرژی فعالسازی آرنیوس و هم ثابت سرعت k بهطور تجربی تعیین میشوند و پارامترهای ویژه واکنش ماکروسکوپی را نشان میدهند که صرفاً به انرژیهای آستانه و موفقیت برخوردهای فردی در سطح مولکولی مربوط نمیشوند.
به عبارت دیگر، انرژی فعال سازی Ea یک کمیت نیمه تجربی است و معنای فیزیکی کاملاً تعریف شده (حداقل در سطح مولکولی) در نظر گرفته نمی شود. توجه داشته باشید که معادله آرنیوس
$k=A\exp\left(-\frac{E_\mathrm a}{RT}\right)$
خود یک رابطه نیمه تجربی در نظر گرفته می شود.
یک پارامتر تجربی که وابستگی نمایی دمای ضریب k را مشخص می کند:
$E_\mathrm a = RT^2 \frac{\mathrm d (\ln k)}{\mathrm dT}$
.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



