دو دیسک چرخان با تکانه زاویه ای یکسان در هنگام تماس کاملاً متوقف می شوند. چرا حرکت زاویه ای در این مورد حفظ نمی شود؟
دو دیسک نصب شده بر روی میله های نازک و سبک وزن مختلف که از طریق مرکز آنها جهت گیری شده اند، طوری ساخته شده اند که به طور جداگانه حول محورهای خود بچرخند، به طوری که تکانه زاویه ای این دو حول محورهای مربوطه خود از نظر قدر و جهت یکسان باشد. هنگامی که هر دو در تماس قرار می گیرند، به دلیل نیروی اصطکاک متوقف می شوند. چرا حرکت زاویه ای در مورد محورهای آنها در این مورد حفظ نمی شود؟ (قبل از تماس مثبت بود، اما پس از تکمیل فرآیند صفر بود، نیروی خارجی نیز وجود نداشت)این دو دیسک یک تکانه (یک تکانه تکانه) را مبادله میکنند که در شعاعهای متفاوتی برای هر دیسک عمل میکند و در نتیجه مقدار حرکت زاویهای متفاوتی مبادله میشود. در پایان، دیسک ممکن است چرخش را متوقف نکنه اما به شکلی سازگار بچرخه (بدون لغزش). اگر دیسک ها را مجبور به توقف کنید در این صورت بقا را نقض می کنید دو دیسک شناور آزاد با چرخش های ناسازگار را در نظر بگیرین جایی که یک دندانه چرخ دنده در نقطه A قرار است در نقطه ای در آینده با هم تماس پیدا کنه
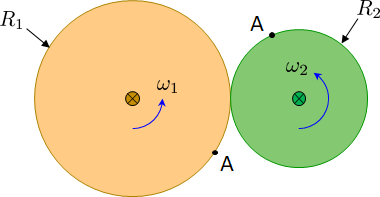
تکانه انتقالی و زاویه ای هر قسمت است
$\begin{aligned} p_1 & = 0 & L_1 & = I_1 \omega_1 \\ p_2 &= 0 & L_2 & = I_2 \omega_2 \\ p_{\rm total} & = 0 & L_{\rm total} &= I_1 \omega_1 + I_2 \omega_2 \end{aligned}$
تکانه زاویه ای کل بدون توجه به نقطه اندازه گیری یکسانه زیرا تکانه انتقالی صفره. بنابراین میتوانیم تکانه زاویهای کل را در مورد نقطه تماس اندازهگیری کنیم.
اکنون تماس زمانی اتفاق می افتد که نقاط A تراز شوند. این باعث یک تکانه برابر و مخالف J می شود روی دو دیسک عمل کند.
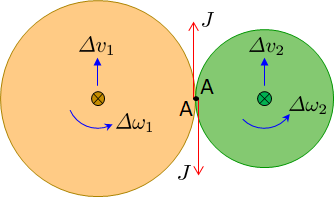
صرف نظر از ارزش J نتیجه فقط تغییر در سرعت زاویه ای $\Delta \omega_1$ و$\Delta \omega_2$نیست بلکه به دست آوردن سرعت انتقالی دو مرکز دیسک $\Delta v_1$ و $\Delta v_2$
دارم $\begin{aligned}
\Delta v_1 & = -\frac{J}{m_1} & \Delta \omega_1 & = -\frac{R_1\,J}{I_1} \\
\Delta v_2 & = +\frac{J}{m_2} & \Delta \omega_2 & = -\frac{R_2\,J}{I_2}
\end{aligned} \tag{1}$
اکنون تغییر حرکت انتقالی و زاویه ای هر قسمت است
$\begin{aligned}
\Delta p_1 & = m_1 \Delta v_1 = J &
\Delta L_1 & = I_1 \Delta \omega_1 - R_1 (m_1 \Delta v_1) = 0\\
\Delta p_2 & = -m_2 \Delta v_2 = -J &
\Delta L_2 & = I_2 \Delta \omega_2 + R_2 (m_2 \Delta v_2) = 0
\end{aligned} \tag{2}$
بنابراین تغییر در تکانه کل انتقالی و زاویه ای است
$\Delta p_1 + \Delta p_2 = J - J = 0 \; \checkmark \tag{3}$
$\Delta L_1 + \Delta L_2 = 0 + 0 \; = 0\checkmark \tag{4}$
بنابراین صرف نظر از مقدار ضربه بقا معتبر است.
حال اگر حالت نهایی نیاز به لغزش ندارد یا $\Delta v_1 + R_1 (\omega_1 + \Delta \omega_1 ) = \Delta v_2-R_2 ( \omega_2 + \Delta \omega_2)$
سپس از سرعت های گام از بالا برای پیدا کردن آن استفاده کنید
$\left( \tfrac{1}{m_1} + \tfrac{R_1^2}{I_1} + \tfrac{1}{m_2} + \tfrac{R_2^2}{I_2} \right) J = R_1 \omega_1 + R_2 \omega_2 \tag{5}$
که برای $J$ حل شده است توجه داشته باشید که حرکت نهایی از (1) با $\omega_1^\text{final} = \omega_1 + \Delta \omega_1$ پیدا می شود
و به طور مشابه برای تمام مقادیر دیگر.نتیجه این است که فقط در شرایط خاص یکی از دیسکها میتواند چرخش را پس از تماس بگیرد اما نه هر دو به طور همزمان. حتی زمانی که دو دیسک یکسان باشند در پایان، مراکز آنها بالا و پایین ترجمه میشوند و چرخش مخالف خواهند داشت.
راه توقف دو دیسک در صورتی است که مرکز آنها به زمین متصل باشد. این را می توان در بالا با $m_1 \rightarrow \infty$و $m_2 \rightarrow \infty$ مدل کرد
. شرط لازم برای توقف دیسک ها پس از ضربه آن است
$\frac{L_1}{L_2} = \frac{I_1 \omega_1}{I_2 \omega_2} = \frac{R_1}{R_2}$
اجازه دهید با این فرض شروع کنیم که دو دیسک دارای تکانه زاویه ای برابر در مورد محورهای خود هستند که برابر با $\vec{L}$ است.
. و بگذارید دو دیسک با سرعت های زاویه ای $\vec{\omega_1}$در حال چرخش باشند
و $\vec{\omega_2}$ از شعاع R1 و R2 با جرم M1 و M2 به ترتیب (برای دیسک های 1 و 2). اجازه دهید ممان اینرسی آنها $I_1$ و $I_2$باشد
در مورد مرکز توده های مربوطه خود. بدین ترتیب$I_1 = \frac{M_1R_1^2}{2}$و
$I_2 = \frac{M_2R_2^2}{2}$و همچنین$\vec{L} = I_1\vec{\omega_1} = I_2\vec{\omega_2} ...(i)$
حال به این سوال میرسیم که حرکت زاویه ای همیشه به محور انتخاب شده بستگی دارد. بنابراین اگر تکانه زاویه ای اولیه و نهایی را حول محور از هر یک از مراکز در نظر بگیریم تکانه زاویه ای به هیچ وجه حفظ نمی شود زیرا یک گشتاور خارجی به دلیل اصطکاک در نقطه تماس مشترک و فاصله بین محور و مشترک آنها عمل می کند. نقطه تماس صفر نخواهد بود.
اما اگر تکانه زاویه ای محور را از طریق نقطه تماس آنها و عمود بر صفحه دیسک ها در نظر بگیریم، باید آن را حفظ کرد زیرا گشتاور صفر خواهد بود زیرا فاصله بین نقطه عمل اصطکاک و محور انتخابی ما صفر خواهد بود.ما می توانیم با حل این موضوع را تأیید کنیم.
از معادله (i) می توان دریافت که سرعت زاویه ای و تکانه زاویه ای همیشه در یک جهت خواهند بود.
اکنون با در نظر گرفتن تکانه زاویه ای اولیه حول محور از طریق نقطه تماسمحاسبه میشه$\vec{L_{net}} = I_1\vec{\omega_1} + I_2\vec{\omega_2}$
توجه: در اینجا $\vec{L_1} = \vec{L_2}$
به عنوان نقطه تماس در وسط راه بین مراکز قرار دارد.
بنابراین با حل به دست می آوریم،
$\vec{L_{net}} = 0$
از این رو حتی اگر چرخش دیسک ها متوقف شود (که لازم نیست) تکانه زاویه ای همچنان 0 خواهد بود و از این رو حفظ می شود. لازم نیست که سرعت های زاویه ای نهایی صفر باشه زیرا به جرم و شعاع آنها بستگی دارد. همچنین انرژی جنبشی دورانی در ابتدا بیشتر از انرژی نهایی خواهد بود. بنابراین انرژی جنبشی حفظ نخواهد شد.


