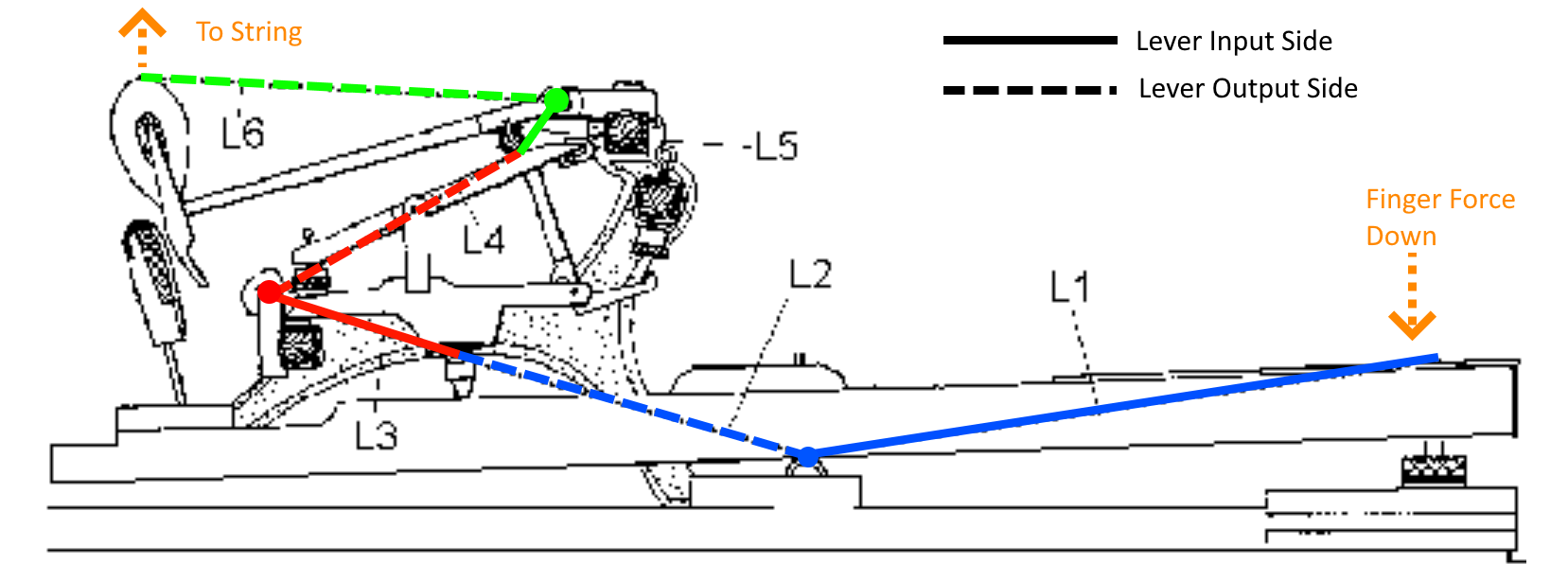
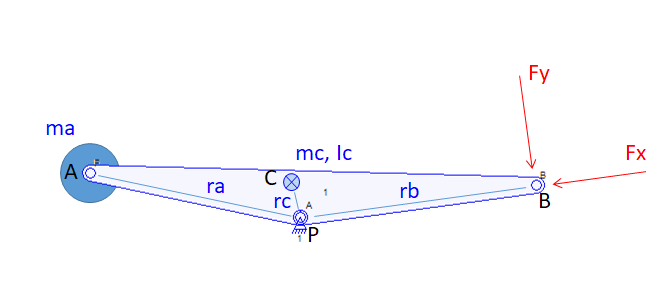
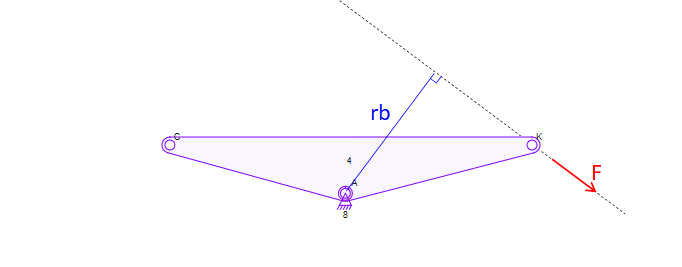
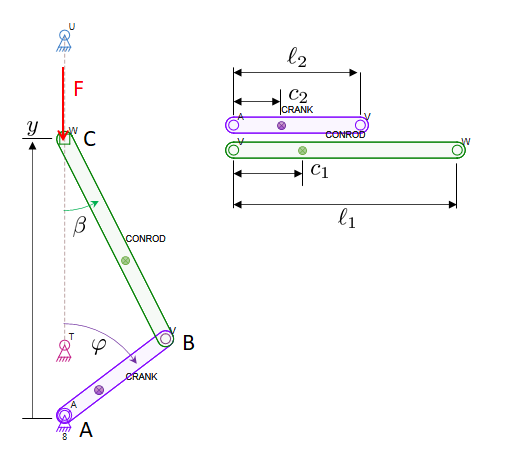
من در حال مطالعه تئوری کنترل هستم و سعی میکنم با استفاده از یک دستکاری ربات مسطح دو پیوندی با یک مثال ساده کار کنم:
هدف من شبیه سازی کنترل PID از دستکاری کننده دو پیوندی مسطح است که در آن هر مفصل توسط یک موتور DC مستقل فعال میشه. ورودی دو سیگنال پیوسته است
$\theta_1(t), \theta_2(t)$
که نمایانگر زاویه مورد نظر برای هر مفصل در زمان t است. مدلسازی یک کنترلکننده برای بازوی رباتیک میتونم بیانی را برای ولتاژی که باید به هر موتور اعمال کنم تا به یک زاویه دلخواه اعمال کنم بدست بیاورم. این مقاله همچنین کنترل کننده PID لازم برای حفظ زاویه مورد نظر را با توجه به سیگنال خطا توصیف میکنه
$e(t) = \theta_{desired}(t)-\theta_{actual}(t)$
از آنجایی که هر موتور به طور مستقل کنترل میشه اثرات کوپلینگ در بین مفاصل به دلیل پیکربندی های مختلف در طول حرکت به عنوان ورودی های اختلال در نظر گرفته میشه سوال من اینه چگونه میتوانم این اثر کوپلینگ را برای شبیه سازی سیگنال خطا e(t) برای سیستم در شرایط ایده آل مدل کنم؟ منظور من از شرایط ایده آل اینه که اختلال ناشی از جفت شدن بین اتصالات 100٪ سیگنال خطا را تشکیل میده.به این ترتیب در زمان t ولتاژ را برای رسیدن به زوایای مورد نظر برای هر موتور مستقل تعیین میکنیم سپس آن را به مدل موتور DC خود وصل میکنم تا گشتاورهای تولید شده را محاسبه کنم
$\tau_1, \tau_2$سپس این گشتاورها را به دینامیک وصل میکنم تا زوایای واقعی را با در نظر گرفتن نیروهای کوپلینگ محاسبه کنم و سپس از زوایای واقعی در مقایسه با زوایای مورد نظر استفاده میکنم تا سیگنال خطایی را ایجاد کنیم که به حلقه کنترل PID تغذیه میکنه
آیا این روشم منطقی است؟ اگر نه کجا اشتباه کرده ام و چگونه میتونم سیگنال خطا ناشی از نیروهای کوپلینگ را شبیه سازی کنم؟
روش کنترل غیر خطی$C(q,\dot{q}) \dot{q}$ اینجا M(q) ماتریس اینرسی است$C(q,\dot{q})$ ماتریس کوریولیس است g(q) بردار گرانشیه و u ورودی من برای کنترلر است.
: هدف این است که پویایی حاصل از سیستم را یکپارچه کننده دوگانه کنیم:$a_{q} = \ddot{q}$
استخراج معادلات حرکت برای فضاپیمای شناور آزاد با بازوی ربات تک پیوندی
من سعی میکنم پویایی یک فضاپیمای شناور آزاد را با بازوی ربات تک پیوندی (گردش) که به یک سر متصل است مدل کنم. من در حال مدل سازی حرکت مسطح و چرخش فضاپیما و پیوند بازوی ربات هستم.
من با فرآیند به دست آوردن دینامیک یک سیستم از طریق فرمول بندی کل انرژی های جنبشی و پتانسیل سیستم و اعمال قضیه اویلر-لاگرانژ آشنا هستم. مشکل این است که من کاملاً مطمئن نیستم که چگونه انرژی های این سیستم را فرموله کنم.
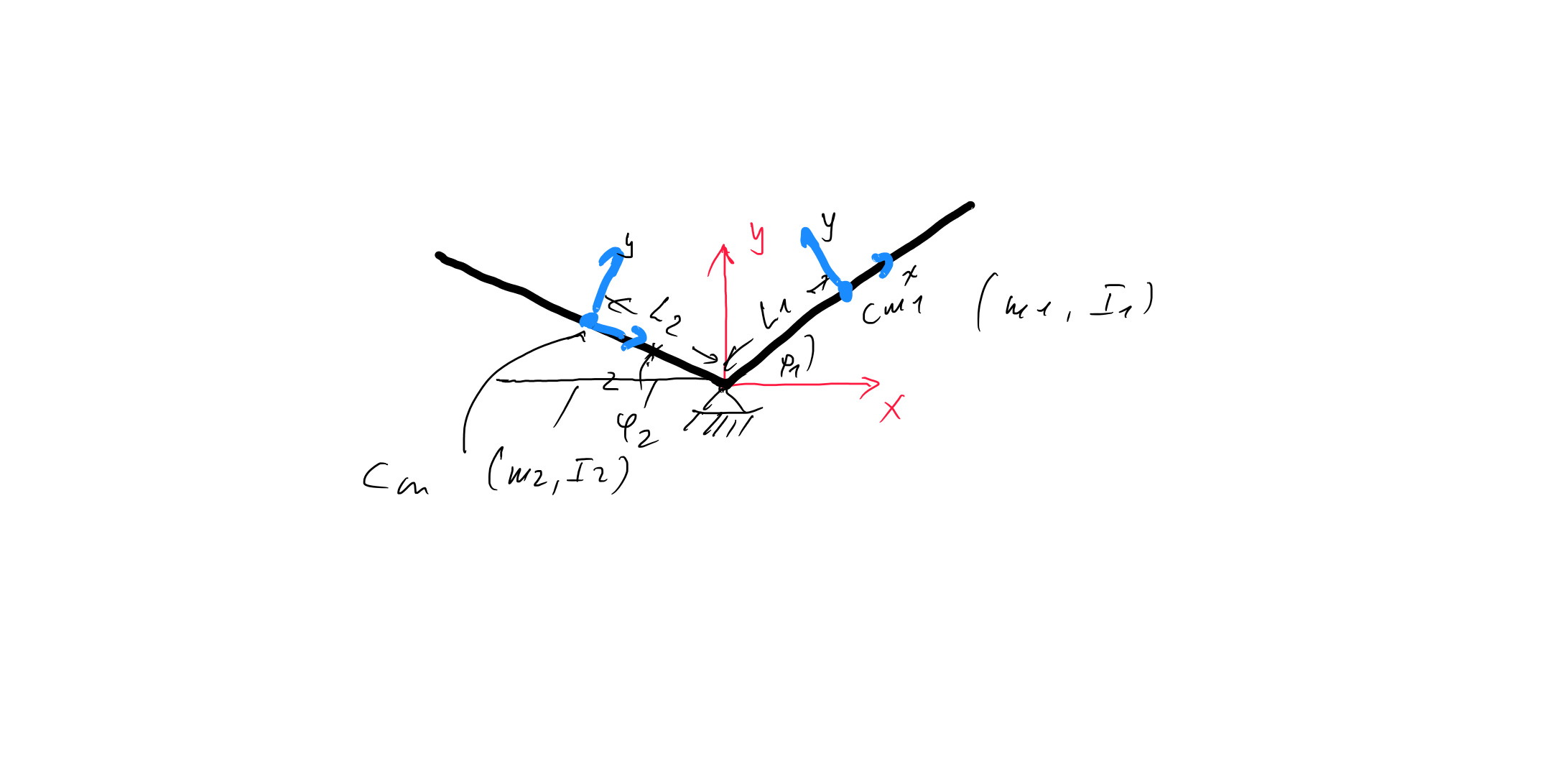
به مدلسازی فضاپیمای خود + سیستم ربات تک پیوندی نگاه کردم که گویی یک سیستم ربات دو پیوندی با یک اتصال چرخشی تک پیوندی 1 با پیوند 2 است. برای سادگی فقط حرکت مسطح را در یک اینرسی در نظر میگیرم. سیستم مختصات بدون نیروهای پتانسیل گرانشی که بر روی سیستم بازوی فضاپیما-ربات عمل میکنه. :
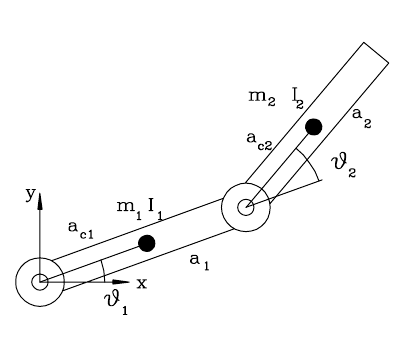
سیستم بازوی ربات دو لینک نصب شده
در یک سیستم ربات پیوند صلب مسطح معمولی با دو مفصل چرخشی که روی یک پلت فرم ثابت نصب شده اند انرژی های پتانسیل ناشی از گرانشه. انرژی های جنبشی برای هر بخش را میتوانم به انرژی های حرکت خطی و از چرخش زاویه ای تجزیه کنم
برای پیوند 1 انرژی جنبشی ناشی از حرکت خطی مرکز ثقل پیوند 1 به حرکت دایره ای محدود میشه زیرا در اتصال 1 به پایه متصله. انرژی خطی آن $$L_1=\frac{1}{2} m_1a_{c1}^2\dot{\theta_1}^2,$$ که $m_1$ جرم پیوند 1 و $a_{c1}$ نیمه طول پیوند 1 است. انرژی دورانی مرتبط با پیوند 1 انرژی حاصل از چرخش حول مرکز جرم آن است. انرژی دورانی آن $$R_1=\frac{1}{2}I_1\dot{\theta_1}^2$$ است که $I_1$ ممان اینرسی پیوند 1 در مورد مرکز جرم آن است. بنابراین کل انرژی جنبشی پیوند 1 $L_1+R_1$ است.
برای پیوند 2 انرژی جنبشی نیز دارای اجزای خطی و چرخشی برای آن است. انرژی خطی را می توان به صورت هندسی با توجه به اینکه موقعیت (x,y) مرکز جرم پیوند 2 را می توان به صورت زیر محاسبه کنم
موقعیت مرکز جرم پیوند 2 $$P_x=a_1cos(\theta_1)+a_{c2}cos(\theta_1+\theta_2)$$ است و
$$P_y=a_1sin(\theta_1)+a_{c2}sin(\theta_1+\theta_2).$$
توجه داشته باشید که $a_1=2*a_{c1}$ طول کامل پیوند 1 و $a_{c2}$ نیمه طول پیوند 2 است.
با استفاده از قانون زنجیره می توان سرعت خطی را در جهت x و y به صورت $\dot{P_x}$ و $\dot{P_y}$ پیدا کرد. سپس انرژی جنبشی ناشی از حرکت خطی در مرکز جرم پیوند 2 $$L_2=\frac{1}{2}m_2v^Tv$$ است که در آن $v=[\dot{P_x} \dot{P_y}] ^T$.
انرژی چرخش مرکز جرم پیوند 2 شامل مجموع سرعت های دورانی هر دو اتصال 1 و 2 است. بنابراین انرژی دورانی حول مرکز جرم پیوند 2 $ R_2=\frac{1}{2}I_2(\ dot{\theta_1}+\dot{\theta_2})^2 $ بنابراین انرژی جنبشی پیوند 2 $K_2=L_2+R_2$ است.
من به جزئیات انرژی پتانسیل نمی پردازم اما اجازه دهید فقط فرض کنیم که عبارت های $P_1$ و $P_2$ برای انرژی های پتانسیل پیوند 1 و پیوند 2 مرتبط با ارتفاع مرکز جرم هر پیوند وجود دارد.
بنابراین برای یک بازوی ربات مسطح گردان دو پیوندی و دو مفصلی میتوانیم لاگرانژ را به صورت $ \mathcal{L}=K_1+K2-P1-P2 = L1+R1+L2+R2-P1-P2 $بنویسیم.
فضاپیمای شناور آزاد با سیستم بازوی ربات تک پیوندی
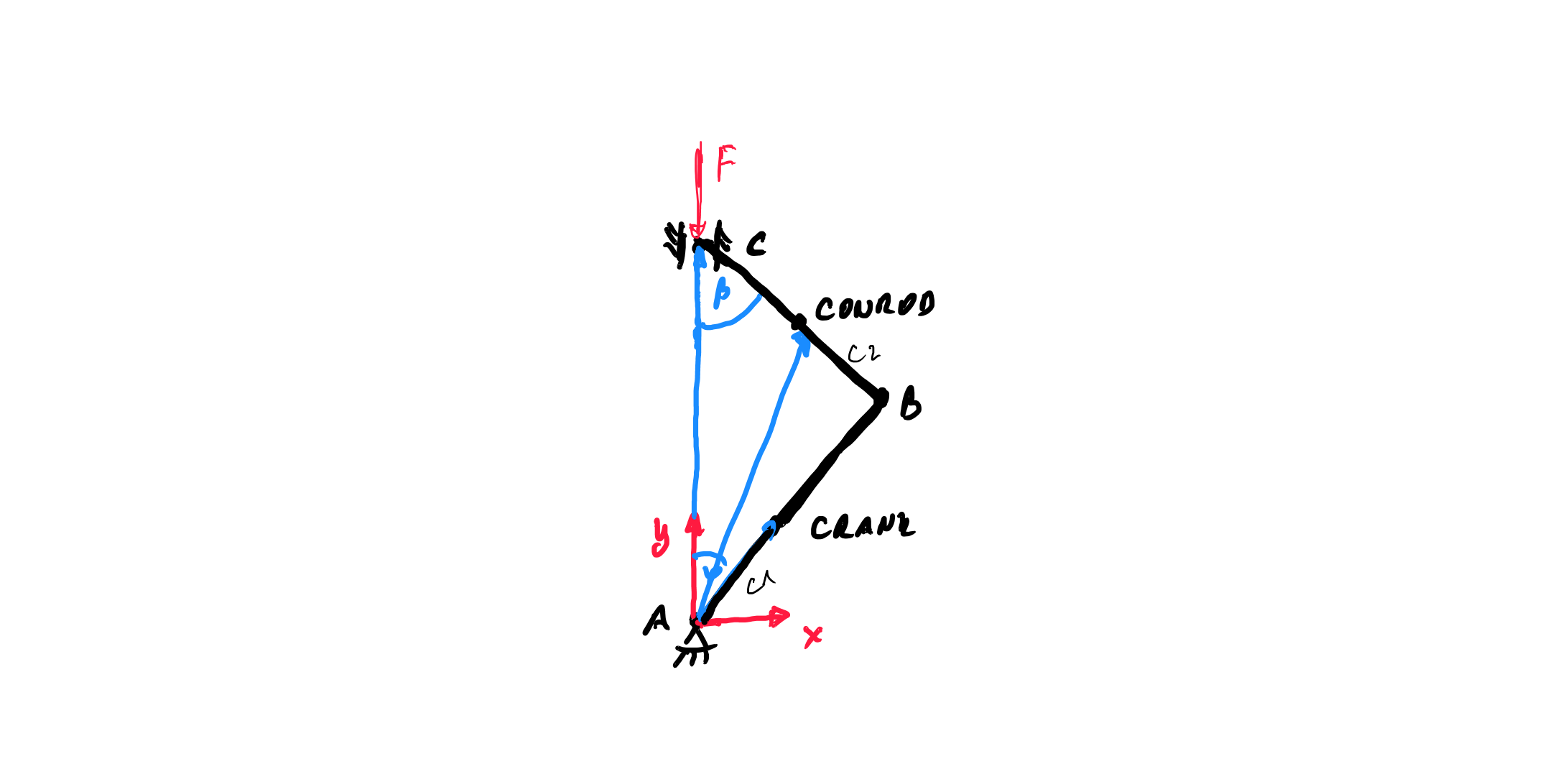
برای به دست آوردن معادلات حرکت برای یک ربات شناور آزاد با یک بازوی رباتی که به یک سر آن متصل است این مدل را انتخاب میکنم و چند تغییر ایجاد میکنم:
فرض کنم لینک 1 یک فضاپیمای شناور آزاد است. بنابراین هیچ مفصل 1 مرتبط با این سیستم وجود نداره
زاویه $\theta_1$ را مجدداً به عنوان زاویه جهت (نگرش) فضاپیما با توجه به یک قاب مرجع اینرسی تعریف کنم.
از آنجایی که سیستم فضاپیما-ربات آزادانه در فضا شناوره من انرژی پتانسیل را برای فضاپیما و روبات صفر فرض میکنم (مثلاً با فرض عدم وجود اثرات گرادیان گرانش یا نیروهای اغتشاش بر روی سیستم). بنابراین $P_1=P_2=0$.
فضاپیما دارای انرژی جنبشی مرتبط با سرعت خطی آن است. با نشان دادن $\dot{x}$ و $\dot{y}$ به عنوان سرعت خطی فضاپیما (پیوند 1) انرژی خطی پیوند 1 تبدیل به $L_1=\frac{1}{2}m_1(\ dot{x}^2+\dot{y}^2).$ میشه فضاپیما همچنین دارای انرژی چرخشی مرتبط با سرعت زاویهای آن $\dot{\theta_1}$ است که توسط $R_1=\frac{1}{1}{1} 2}I_1\dot{\theta_1}^2$
سوال من
من مطمئن نیستم که عبارات انرژی خطی و چرخشی را در پیوند 2 به درستی توصیف میکنم یا خیر. من فرض میکنم مرکز جرم پیوند 2 (بازوی ربات) دارای موقعیت (x,y) است که توسط:
$P_x = x + a_{c1}cos(\theta_1)+a_{c2}cos(\theta_1+\theta_2)$و$P_y = y + a_{c1}sin(\theta_1)+a_{c2}sin (\theta_1+\theta_2)$ بنابراین اگر من مشتقات زمانی $P_x$ و $P_y$ را مانند قبل در نظر بگیرم باید عبارتی برای سرعت $v=[\dot{P_x},\dot{P_y}] $ محاسبه کنم و انرژی جنبشی ناشی از حرکت خطی باید be $L_2=\frac{1}{2}m_2v^Tv$.
سوال 1:
آیا انرژی جنبشی پیوند 2 (بازوی ربات) باید شامل عباراتی با سرعت فضاپیما (پیوند 1) $\dot{x}$ و $\dot{y}$ در آن باشه؟ ذهن من مدام در مورد اینکه آیا باید سرعت فضاپیما را به عنوان بخشی از انرژی بازوی ربات لحاظ کنم یا خیر به عقب و جلو می رود.
سوال 2:
آیا انرژی دورانی فقط باید شامل مجموع سرعت های زاویه ای موقعیت فضاپیما ($\dot{\theta_1}$) و مفصل بازوی ربات $\dot{\theta_2}$ باشه. به طور خاص آیا نوشتن $R_2=\frac{1}{2}I_2(\dot{\theta_1}+\dot{\theta_2})^2$ صحیح است؟ من شک دارم که انرژی انرژی چرخشی پیوند باید مانند مورد بازوی ربات دو پیوندی پایه ثابت باشه اما به نظر نمیرسد هیچ منبع پتانسیل دیگری برای انرژی دورانی پیدا کنم.
آیا عبارات من برای $P_x$ $P_y$ و $R_2$ برای جعبه بازوی فضاپیما-ربات صحیح است؟ اگر نه کجا اشتباه کردم یا چه چیزی را از فراموش کردم؟
من گفتم میدان گرانشی وجود نداره فنر وجود نداره خمش بدنه وجود نداره اصطکاک وجود نداره - معلوم نیست چه دینامیکی را انتظار دارم که از این مشکل خلاص بشم!
حتی فراتر از آن باقی فرض روشن نیست. من در سوال 1 اشاره کردم که فضاپیما پیوند 1 است اما پس از آن پین کردن لینک 1 چیست؟ قبلا در متن سوال خودم گفتم
من به مدل سازی فضاپیمای خود + سیستم ربات تک پیوندی نگاه کردم که گویی یک سیستم ربات دو پیوندی با یک اتصال چرخشی منفرد پیوند 1 با پیوند 2 است.
اما در ادامه می گویید:
برای پیوند 1 انرژی جنبشی ناشی از حرکت خطی مرکز ثقل پیوند 1 به حرکت دایره ای محدود میشود زیرا در اتصال 1 به پایه متصله
دوباره من شروع می کنم و می گویید که فقط یک مفصل وجود داره سپس آن دو مفصل و یک پلت فرم ثابته
در مورد خود سوال 1: اگر لینک 1 دارای سرعت باشه و لینک 2 به لینک 1 متصل باشه لینک 2 نیز دارای آن سرعت است. تنها تفاوت سرعت در نتیجه هر حرکت در اتصال بین پیوندهای 1 و 2 خواهد بود.
در مورد سوال 2 انرژی چرخشی دقیقا وجود نداره انرژی جنبشی و انرژی پتانسیل وجود دارد. هر انرژی جنبشی دورانی با دیگر اصطلاحات انرژی جنبشی گروه بندی می شود. یعنی پیوند 1 دارای مجموع انرژی جنبشی خود و پیوند 2 دارای مجموع انرژی جنبشی خود است.
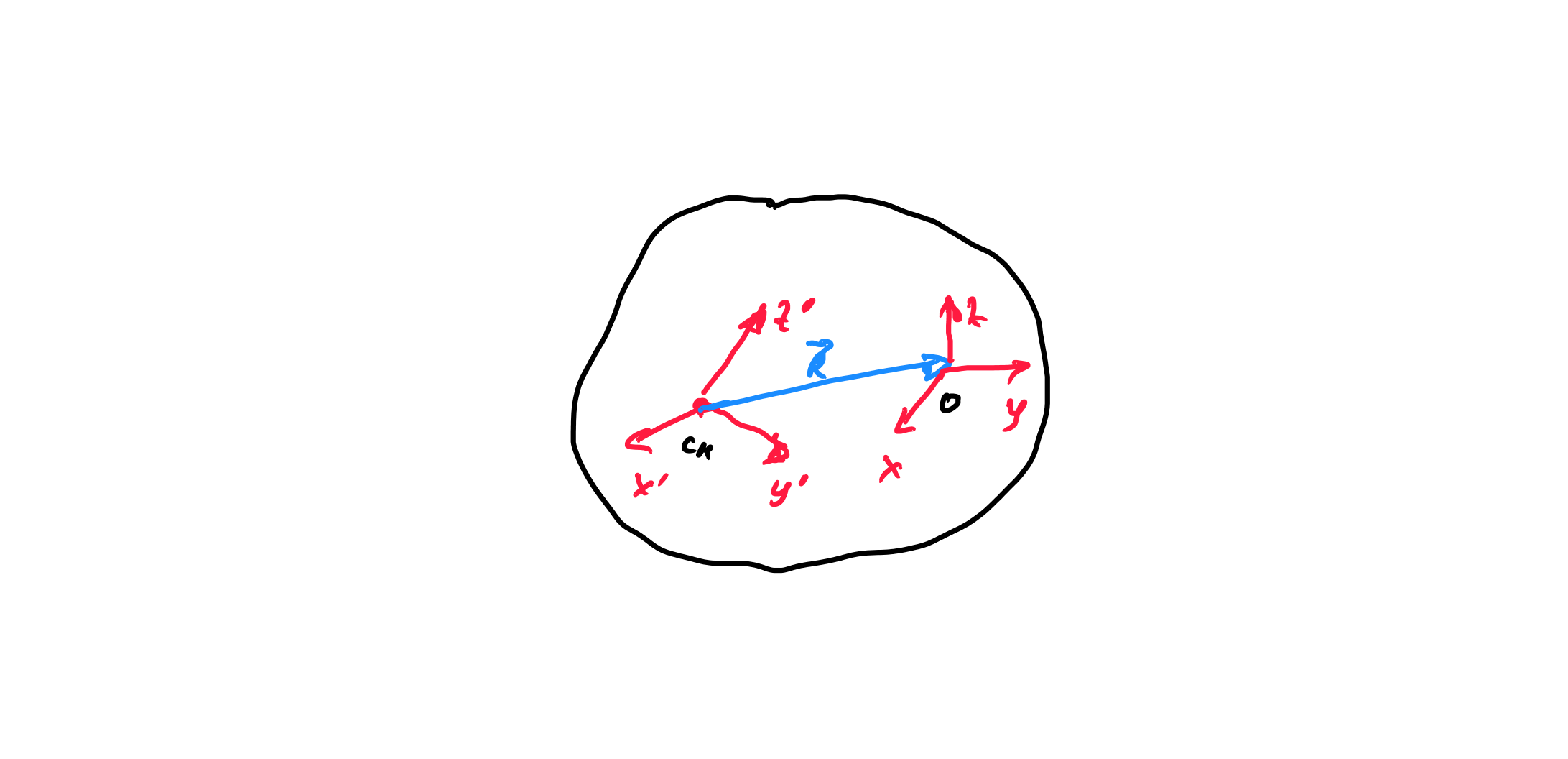
از آنجایی که من واقعاً یک پلت فرم ثابت ندارم (یا دارم؟) پیوند 1 من قرار نیست حول اولین مفصل بچرخد. در عوض کل سیستم حول مرکز جرم سیستم می چرخد. سپس مکان آن مرکز جرم به نسبت جرم ها و زاویه اتصال بستگی دارد.
شاید همانطور که در ابتدا اشاره کردم بهتر است آنچه را که می خواهید مطالعه کنم روشن کنم و از آن به عنوان ابزاری برای راهنمایی بقیه رویکرد خود استفاده کنم. من فکر میکنم من باید به دنبال اعمال بقای تکانه خطی و حفظ تکانه زاویه ای برای سیستم به عنوان یک کل باشم و سپس سعی کنم داده مرجع و سایر اصطلاحات خود را به گونه ای تعریف کنم که بهترین روش را پشتیبانی کند.
من نمی توانم بیشتر از این کمک کنم زیرا دوباره مطمئن نیستم که تنظیمات دقیق سؤال را دنبال کنم. با این حال من می گویم که فکر میکنم تعریف مجدد داده مرجع من (نسبت به m1 یا m2) یک اشتباه است. این سیستم دارای یک مرکز جرم است. حرکت زاویه ای و خطی سیستم حفظ شده است بنابراین احتمالاً باید به دنبال تعریف هر چیز دیگری نسبت به مرکز جرم سیستم باشم. سپس باید شروع کنم به یافتن چیزهایی مانند سرعت های انتقالی فقط نسبت جرم ها و غیره زیرا باید اجزای عمودی افقی و زاویه ای تکانه را ثابت نگه دارم. این محدودیت ها (همراه با محدودیت سینماتیک مفصل) نحوه حل مشکل من هستند.
معادلات حرکت ربات
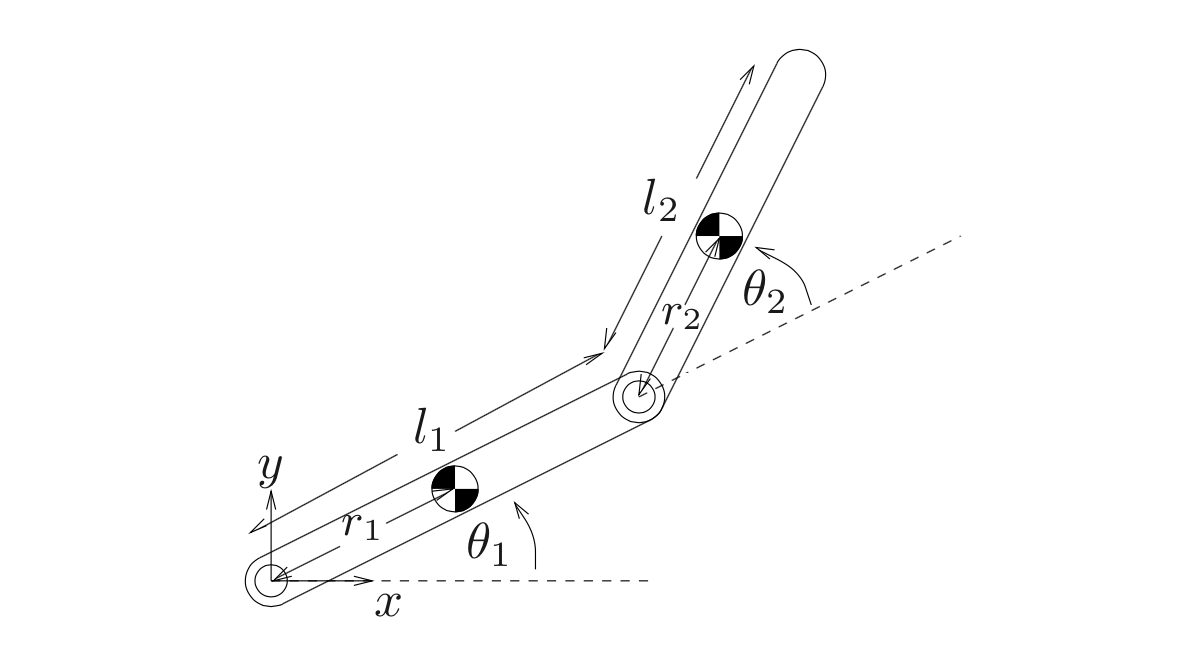
مدل بازوی رباتیک دو لینکی
. این پیکربندی را میتونم به عنوان آونگ دوگانه نیز در نظر بگیرم فرض میکنیم طول لینکهای بدون جرم $l _ 1$.و$l _ 2$ بوده و به انتهای هریک از آنها به ترتیب جرمهای $m_ 1$و$m _ 2$ متصل شده باشه. زوایای $\theta _ 1$ و$\theta _ 2$
فرض میکنیم برای هر مفصل یک موتور وجود داشته باشه
بازوی رباتیک دو لینکی ساده یا آونگ دوگانه دربازوی رباتیک دو لینکی ساده یا آونگ دوگانه$\theta _ 1$ و$\theta _ 2$ زاویههای برای توصیف مناسب سیستم انتخاب شدهاند. زیرا در این نوع نمایش به تعداد حداقل متغیرهای مستقل برای توصیف کامل سیستم نیاز است. میتونم از موقعیتهای x و y جرمها نیز برای به دست آوردن معادلات حرکت استفاده کرد. البته در این روش محدودیتهای بیشتری را باید روی سیستم اعمال کرد تا تضمین شود طول لینکها ثابت میماند. چنین محدودیتها و قیودی با اعمال محدودیتهای پفافی (Pfaffin constraints) اعمال میشوند.
. در سیستمهای رباتیک پیچیده یا شبیهسازیهای بیومکانیکی موقعیت بردارها را میتونم با استفاده از نظریه پیچها (Screw Theory) یا پارامترهای دناویت-هارتنبرگ (Denavit–Hartenberg Parameters) به دست آورد. با استفاده از دستگاه مختصات مناسب میتونممعادلات حرکت را بسیار ساده کرد. البته این کار شاید همیشه ممکن نباشه. برای مثال مدل راه رفتن انسان با کف پای قوسی را نمیتونمبا چشمپوشی از قیود موقعیت و سرعت بین پا و زمین مدل کرد.یک ربات دوپای هفتلینکی با پای قوسی : یک ربات دوپای هفتلینکی با پای قوسی در ادامه معادلات حرکت را با استفاده از روش لاگرانژ به دست خواهم آورد.محاسبه موقعیت و سرعت
اولین گام محاسبه موقعیت همه اجرام سیستم است. در اینجا موقعیت جرمها را نسبت به مرکزی که به پایه بازو الصاق شده و برحسب زوایای $\theta _ 1$ و$\theta _ 2$
محاسبه میکنیم:$\large \left [ \begin {array} { c } P _ { 1 , x } \\ P _ { 1 , y } \end {array} \right ] = \left [ \begin {array} { c } l _ 1 \cos ( \theta _ 1 ) \\ l _ 1 \sin ( \theta _ 1 ) \end {array} \right ]$
و$\large \left [ \begin {array} { c } P _ { 2 , x } \\ P _ { 2 , y } \end {array} \right ] = \left [ \begin {array} { c } l _ 1 \cos ( \theta _ 1 ) + l _ 2 \cos ( \theta _ 1 + \theta _ 2 ) \\ l _ 1 \sin ( \theta _ 1 ) + l _ 2 \sin ( \theta _ 1 + \theta _ 2 ) \end {array} \right ] .$
سپس سرعت را با استفاده از معادلات بالا به دست میآوریم:
$\large v = \frac { d P } { d t } = \frac { \partial P } { \partial \theta _ 1 } \dot { \theta } _ 1 + \frac { \partial P } { \partial \theta _ 2 } \dot { \theta } _ 2$
محاسبه انرژی جنبشی و انرژی پتانسیل سیستم
در این بخش انرژی جنبشی و پتانسیل سیستم را محاسبه میکنم. انرژی جنبشی به صورت زیره
$\large KE = \frac { 1 } { 2 } m _ 1 v _ 1 ^ T v _ 1 + \frac { 1 } { 2 } m _ 2 v _ 2 ^ T v _ 2$
انرژی پتانسیل نیز به صورت زیر تعریف میشه
$\large PE = m _ 1 g P _ { 1 , y } + m _ 2 g P _ { 2 , y }$
استخراج معادلات حرکت ربات برای به دست آوردن معادلات حرکت ابتدا لاگرانژین L را تشکیل میدهیم:$\large L = KE - PE$
سپس معادلات حرکت با کمک رابطه زیر به دست میآیند:$\large \frac { d } { d t } \left ( \frac { \partial L } { \partial \dot { q } } \right ) - \frac { \partial L } { \partial q } = \tau$
که در آن $q = [ \theta_1, \theta_2]^T$ بردار موقعیت و سرعت زاویهای است و $\tau$
بردار گشتاورهای اعمالی توسط موتورها در دو مفصل است. پس از مرتبسازی جملات معادلات حرکت را میتونمبه صورت زیر نوشت:
$\large D ( q ) \ddot { q } + C ( q , \dot { q } ) \dot { q } + G ( q ) = \tau$ یا$\large \ddot { q } = D ( q ) ^ { - 1 } ( \tau - C ( q , \dot { q } ) \dot { q } - G ( q ) )$
میتوانیم معادله بالا را به صورت زیر بازنویسی کنیم:$\large \ddot { q } = \alpha ( q , \dot { q } ) + \beta ( q ) \tau$
که در آن $\alpha ( q , \dot { q } ) = D ( q ) ^ { - 1 } ( - C ( q , \dot { q } ) \dot { q } - G ( q ) )$
این فرم معادله در کنترل بسیاری از سیستمهای غیرخطی معمول است. دستههای خاص سیستمهای بالا که در آنها ورودی یک جمله خطی اضافه دارد فرم کنترل-افاین (Control-Affine Form) نامیده میشه
خطیسازی معادلات حرکت ربات
هرچند همه سیستمهای موجود در طبیعت غیرخطی هستند اما میتونمسیستم را با یک سیستم خطی از معادلات تحت فرضیات مشخصی خطی کرد. یکی از فرضیات اصلی این است که اندازه موقعیت و سرعت سیستم کم است.
این مورد در مثالهایی که پایدارسازی سیستم در برابر آشفتگیهای خارجی مورد نظر است رواج دارد. برای مثال اگر بخواهیم ربات با دو مفصل را در موقعیت مشخص
q_0$$ نگه داریم آنگاه باید فرض کنیم که نتیجه آشفتگیهای خارجی کوچک است. بنابراین میتوانیم از سری تیلور به صورت ماتریسی حول نقطه پایدار $q _ 0$ استفاده کنیم. سیستم در $q _ 0$
و $\dot {q } = 0$ ¨و$\ddot { q} = 0$ در تعادل است. بنابراین خواهیم داشت:$\large 0 = \alpha ( q _ 0 , 0 ) + \beta ( q _ 0 ) \tau _ 0 ,$
یا$\large \tau _ 0 = - \beta ( q _ 0 ) ^ { - 1 } \alpha ( q _ 0 , 0 ) .$ از بسط تیلور برای یک تابع دومتغیره استفاده میکنیم:
$\large f ( x + \delta x , y + \delta y ) \approx f ( x , y ) + \left . \frac { \partial f } { \partial x } \right | _ { ( x , y ) } \delta x + \left . \frac { \partial f } { \partial y } \right | _ { ( x , y ) } \delta y .$ با استفاده از معادله بالا حول $q = q_0$ و$\dot{q} = 0$ داریم:
$\large \begin {align*}\delta \ddot { q } & = \alpha ( q _ 0 , 0 ) + \left . \frac { \partial \alpha } { \partial q } \right | _ { ( q _ 0 , 0 ) } \delta q + \left . \frac { \partial \alpha } { \partial q } \right | _ { ( q _ 0 , 0 ) } \delta \dot { q } \\ & + \left ( \beta ( q _ 0 , 0 ) + \left . \frac { \partial \beta } { \partial q } \right | _ { ( q _ 0 , 0 ) } \delta q \right ) \left ( \tau _ 0 + \delta \tau _ 0 \right ) + H.O.T \end {align*}$
با بازآرایی و صرفنظر کردن از جملات مرتبه بالاتر خواهیم داشت:
$\large \delta \ddot { q } = \underbrace { \left . \frac { \partial \alpha } { \partial q } \right | _ { ( q _ 0 , 0 ) } \delta q + \left . \frac { \partial \alpha } { \partial q } \right | _ { ( q _ 0 , 0 ) } \delta \dot { q } + \left . \frac { \partial \beta } { \partial q } \right | _ { ( q _ 0 , 0 ) } \delta q \tau _ 0 } _ { \text {Linear in } \delta q \text { and } \delta \dot { q } } + \underbrace { \beta ( q _ 0 ) \delta \tau _ 0 } _ { \text {Linear in } \delta \tau _ 0 }$
بنابراین معادلات حرکت را میتونمبا یک سیستم دینامیکی خطی سادهتر حول $q _ 0$ و$\dot { q } = 0$ بیان کرد.
در مواردی که سیستم افاین نیست بسط تیلور را میتونمبه صورت زیر مورد استفاده قرار داد:$\large \ddot q _ 0 + \delta \ddot q = f ( q _ 0 + \delta q , u _ 0 + \delta u ) \approx f ( q _ 0 , u _ 0 ) + \left. \frac { \partial f } { \partial q } \right | _ { ( q _ 0 , u _ 0 ) } \delta q + \left . \frac { \partial f } { \partial u } \right | _ { ( q _ 0 , u _ 0 ) } \delta u .$
با در نظر گرفتن $\ddot q_0 = f(q_0 ,u_0)$
داریم:$\large \delta \ddot q = \left . \frac { \partial f } { \partial q } \right | _ { ( q _ 0 , u _ 0 ) } \delta q + \left . \frac { \partial f } { \partial u } \right | _ { ( q _ 0 , u _ 0 ) } \delta u .$