من فکر میکنم یک شرایط مرزی همرفت طبیعی را می توان در محدوده جریان آرام فرض کرد و حداکثر دما نباید از 100 ∘ تجاوز کنه.
از آنجایی که توزیع دمای سطح یکنواخت نیست هر گره سطح باید ضریب انتقال حرارت همرفتی منحصر به فرد خود را داشته باشه (h) زیرا این پارامتر به اختلاف دمای دیواره جامد و سیال بستگی داره.
اما با جستجوی چند کتاب درسی انتقال حرارت هرگز ندیدم که دانشجویان مثل من این مشکل رو این شکل تحلیل کنند. من فقط برخی از را حلها و معادلات همبستگی را در روش توزیع دمای یکنواخت هندسه های مختلف پیدا کردم در حالی که در شبیه سازی من دمای گره های سطحی مختلف متفاوته. با کمی فکر متوجه شدم که ضریب انتقال حرارت جابجایی به خواص سیال وابستیه که آن را بسیار پیچیده میکنه
پس آیا می توان چنین محاسباتی را با روش تفاضل محدود انجام داد؟ آیا روشی برای حداقل تخمین ضریب انتقال حرارت همرفتی وجود داره؟روش من کاملا قابل قبوله تا زمانی که محدودیت های آن را درک کنم. دلیل اینکه شما چنین روشی را در یک کتاب درسی نمیبینم اینه که ترکیبی از روش های عددی و روش های تجربی مرسوم است که به خصوص رایج نیست.
دلیل اینکه به این شکل به مشکل برخورد نمیشه این که ضریب انتقال حرارت جابجایی طبیعی (htc) یک خاصیت حجیمه. این بر اساس هندسه کلی است و قراره پیش بینی انتقال حرارت در کل سطح جسم را به من ارائه کنه. بنابراین htc بر اساس هندسه و خصوصیات کلی سیستم است و نه هندسه محلی و خصوصیات درست در اطراف هر گره. امیدوارم این تصویر منظورمو برسونه
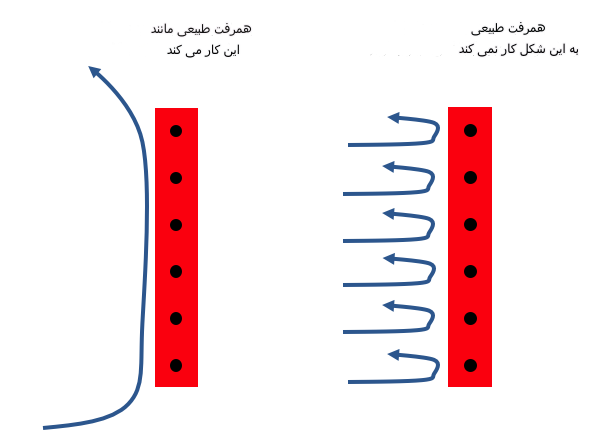
در اینجا یک صفحه داغ در مقداری مایع سرد دارم. من صفحه داغ را به 6 گره تقسیم کرده ام تا دمای سطح را تخمین بزنم، اما نمیتونم htc را تنها بر اساس دمای هر گره محاسبه کنم زیرا این روشی نیست که همرفت طبیعی کار میکنه
قوی ترین راه برای حل این مسئله حل عددی همرفت طبیعیه. این همان کاری است CFD مانند comsol انجام میده. با این حال این نیاز به مدل سازی عددی سیال داره که همانطور که در بالا گفتید بسیار پیچیده خواهد شد.
روش دیگه اینهکه به استفاده از htc انبوه ادامه دهم اما هر بار که از طریق اعداد داخلی خود تکرار میکنم آن را دوباره محاسبه کنم سپس یک htc حجیم ایجاد میکنم و میتونم از طریق Q=dA*htc*(T_i-T_bulk) تلفات حرارتی هر گره را محاسبه کنم. هنگامی که حل کننده خود را اجرا میکنم فقط باید htc را بر اساس میانگین دمای سطح جدید در هر تکرار دوباره محاسبه کنم
اما موضوع اصلی اینه که محدودیت های هر سازشی را که انجام میدم میدونم. استفاده از htc حجیم اگر سیالم Cp بالایی داشته باشه و در نتیجه وقتی روی مکعب جریان مییابه dT زیادی نخواهد داشت یک حرکت خوبه همچنین اگر هندسه یک مکعب یا کره باشه که در آن آب برای مدت طولانی روی قسمت جریان نداشته باشه حرکت خوبیه اگر سیالم Cp پایینی داشته باشه و بنابراین هنگام عبور از قطعه شما دارای dT بزرگ باشه یا اگر قطعه مسیر جریان بسیار طولانی داشته باشه زیرا تغییر در وظیفه ناشی از تغییر dT را نشان نمیده این روش خوبی نخواهد بود. بین اولین و آخرین گره آب از کنار آن عبور میکنه
در مجموع من فکر میکنم مدل به اندازه کافی ساده هستش باید انالیزش کنمکه چه نتایجی حاصل میشه سپس میتونم دمایی را که برای دمای حجیم استفاده میکنم شروع کنم تا سعی کنم دمای آب را بهتر ثبت کنم.
اجرای شرایط مرزی همرفتی برای محاسبه تفاضل محدود 1 بعدی معادله گرما
من در حال شبیه سازی انتقال حرارت از طریق یک دیوار 1 بعدی با همرفت در دو طرف هستم. برای دیوار من یک مدل تفاضل محدود به این صورت پیادهسازی کردم
$u(x, t + ∆t) ≈ u(x, t) + c [u(x + ∆x, t) − 2u(x, t) + u(x − ∆x, t)]$
که در آن $c = α \frac{∆t}{(∆x)^2}$ و $α$ انتشار حرارتیه. اگر فقط به دیوار نگاه کنم و فرض کنم دمای دو سر دیوار همیشه مشخصه اجرای این مدل خوب کار میکنه. اکنون میخواهم مدل را به گونهای گسترش دهم که همرفت در دو طرف دیوار را شامل بشه. به نظر می رسد بهترین راه برای انجام آن استفاده از شرایط مرزی همرفتیه
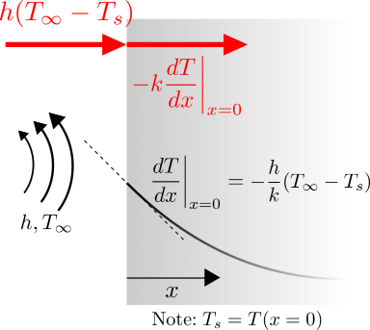
$T_{\infty}$ و h از هر دو طرف شناخته شده هستن اما در طول زمان متغیرند. $k$ شناخته شده و ثابته من در تلاش برای یافتن نقطه شروعی برای اجرای این شرایط مرزی به عنوان بسط مدل فوق هستم.
به طور شهودی من حدس میزنم که برای x=0 ، معادله بالا باید چیزی شبیه به این باشه$u(0, t + ∆t) ≈ u(0, t) + c [u(0 + ∆x, t) − 2u(0, t)] + a * T_{\infty}$
جایی که a تابعی از h است و Δt. و برای x=L، باید از یک معادله مشابه استفاده بشه آیا میتونه درست باشه؟
فرض کنم من فضا را به n تقسیم میکنم پارتیشن های مساوی به طوری که $\Delta x=\frac{L}{n}$و. n+1 وجود داره گره ها که با $x_i$ مشخص میشوند جایی $i=(0,1,....n)$ . هدف یافتن $u_i=u(x_i)$ است. در هر زمان اجازه میدم $u_i^j$ مقدار دما را در $x_i$ نشون میده در مرحله زمانی j . من شرایط اولیه را ذکر نمیکنم بنابراین من فرض میکنم که در ابتدا همه چیز در محیط $T_{\infty}$ است به طوری که $u_i^0=T_{\infty} \forall i$ . هدف زمانی برای به دست آوردن$u^{j+1}_i$ است با توجه به$u_i^j$ . اجازه میدم قبل از BC را در سمت چپ مشاهده کنم. دارم$\frac{\partial u}{\partial x}(x=0)=-b(T_{\infty}-u(x=0))$ . با تفکیک آن،$u_{1}^j-u_{-1}^j=-b(T_{\infty}-u_0^j)$را دریافت میکنم.. میدونم که من Δx را جذب کرده ام در b. اینجا $u_{-1}$ مربوط به یک نقطه خیالی و فرضی هست نقطه ای در فضا که وجود نداره اما برای راحتی ریاضی فرض میشود میدونم که لبه سمت چپ $x_0$ است.). به طور مشابه میتونم یک معادله گسسته برای دیوار سمت راست بنویسم اکنون به طرح پله زمانی خودم نگاه کنم
$u_i^{j+1}=u_i^j+c(u_{i+1}^j-2u_i^j+u_{-1}^j)$ از j=0 شروع کنم سمت راست را برای j=0 (شرایط اولیه ام زمانی که $ i=1,2.....(n-1)$. بنابراین من $u_i^{1}$را دریافت میکنم
وقتی$i=1,2,3...(n-1)$وقتی i=0، در نهایت به $u_{-1}^0$نیاز دارم که با شرط اولیه داده نمیشه (توجه داشته باشید که $u_{-1}^0\neq T_{\infty}$
، این برابری فقط برای نقاط فیزیکی معتبره و نه نقاط فرضیام اما به راحتی میتوانم آن را از قبل از BC بدست بیارم ومحاسبه کنم من میدونم که$u_{-1}^0=u_1^0+b(T_{\infty}-u_0^0)$
من باید این روش را دوباره برای i=n تکرار کنم جایی که به نقطه فرضی دیگری $u_{n+1}$ نیاز دارم که مقدار آن از نظر نقاط فیزیکی با استفاده از دیوار سمت راست قبل از BC محاسبه ومشاهده میشه
من الان میدونم $u^1_i \forall i \in (0,n)$
.


