سرعت و سرعت زاویه ای
در حرکت دایره ای یکنواخت سرعت زاویه ای (𝒘) یک کمیت برداری است و برابر است با جابجایی زاویه ای (Δ𝚹 کمیت برداری) تقسیم بر تغییر زمان (Δ𝐭). سرعت برابر است با طول پیموده شده قوس (S) تقسیم بر تغییر زمان (Δ𝐭) جسمی که سرعت خطی یکسانی دارد یک فاصله مشخص را در زمان معین پوشش می دهد و جسمی با سرعت زاویه ای زاویه خاصی (نه فاصله) را در واحد زمان پوشش می دهد. در مثال ساعت نوک عقربه سریعتر حرکت میکند زیرا سرعت خطی سریعتری دارد اما سرعت زاویهای یکسانی دارد. بگذارید فاصله افقی تا نوک ساعت y و فاصله افقی باشد (فاصله بین نقاطی که y با منشاء افقی و عقربه برش می دهد x باشد). حال tanθ=y/x که به معنای θ=tan − 1 y/x است بنابراین اگر x را افزایش دهیدy باید بر این اساس افزایش یابد تا زاویه θ حفظ شود. بنابراین x بالاتر y و پایین x پایین yجسمی که سرعت خطی یکسانی دارد یک فاصله مشخص را در زمان معین پوشش می دهد و جسمی با سرعت زاویه ای زاویه خاصی (نه فاصله) را در واحد زمان پوشش می دهد. در مثال ساعت نوک عقربه سریعتر حرکت میکند زیرا سرعت خطی سریعتری دارد اما سرعت زاویهای یکسانی دارد. $\omega = \dfrac{\theta}{t}.$و$v = \dfrac{s}{t} = \dfrac{r\theta}{t}$
$\omega = x \dfrac{rev}{min} \cdot \dfrac{2\pi rad}{rev} = x(2\pi)\dfrac{rad}{min}.$
پاسخ ساده از هندسه می دانید که طول یک کمان s=rθ است جایی که r شعاع قوس است و θ زاویه ای که می گذرد مشتق زمانی از موارد فوق را در نظر بگیرید زیرا قوس حرکت ذره ای را که بر روی یک جسم در حال چرخش سوار می شود توصیف می کند و شما
$$v = r \, \omegaجایی که $\omega = \frac{\rm d}{{\rm d}t} \theta$
. همچنین r بازوی لحظه ای حرکت است که به طور آنی ثابت است (مقدار آن در بازه های زمانی کوچک ثابت می ماند).
درک عمیق
امیدوارم با بردارها آشنایی داشته باشید زیرا در این سطح سینماتیک (مطالعه حرکت) به جای در سطح مؤلفه شهودی تر می شود. به طور خاص شما باید با مفهوم ضربدری و حاصلضرب نقطه بین دو بردار آشنا باشید. مهمتر از آن اینکه بیانی از شکل (موقعیت)×(چیزی)
ما را با مفهوم بازوی اهرمی آشنا می کند.
همراه با بازوی اهرمی مفهوم لحظه از می آید. جایی که گشتاور لحظه نیروی $\vec{\tau} = \vec{r} \times \vec{F}$ است
و سرعت انتقالی لحظه چرخش است $\vec{v} = \vec{r} \times \vec{\omega}$
.بیایید در مورد سرعت چرخشی (وکتور) $\vec{\omega}$ صحبت کنم
من از سه جنبه مختلف حرکت برای صحبت در مورد سرعت چرخشی استفاده خواهم کرد.
[سینماتیک] $\vec{\omega}$
یک ابزار ریاضی برای ساده کردن توصیف حرکت یک جسم صلب است. به جای تعیین بردارهای سرعت در هر نقطه از جسم سرعت چرخشی به ما امکان محاسبه راحت با استفاده از سرعت یک نقطه برای تخمین سرعت تمام نقاط دیگر را می دهد.
$\vec{v}_{\rm point} = \vec{v}_{\rm ref} + \vec{\omega} \times \vec{r}$
[فیلد برداری] $\vec{\omega}$
تجسم دشوار است زیرا بر خلاف سرعت انتقالی $\vec{v}$ مستقیماً از روی حرکت مشاهده شده قابل اندازه گیری است.
که به طور مستقیم در هر نقطه قابل اندازه گیری است. سنجش چرخشی موضوعی جذاب است. اما بدانید که حرکت کلی واقعی یک جسم صلب با یک سرعت vec توصیف میشه دفیلد tor با هر دو جزء دوار و مولفه انقال موازی. به این قضیه Chasles گفته میشه. یک جسم صلب را در نظر می گیرد که ابتدا یک چرخش حول محوری که از مرکز جرم می گذرد و سپس جابجایی D را در جهت دلخواه تغییر می دهد. هر حرکت صلب را می توان به این طریق به دلیل قضیه ای که اویلر در مورد وجود یک محور چرخش انجام داد انجام داد. جابجایی D مرکز جرم را می توان به اجزای موازی و عمود بر محور تجزیه کرد. مولفه عمود بر (و موازی) روی تمام نقاط جسم صلب عمل می کند اما موزی نشان می دهد که برای برخی از نقاط چرخش قبلی دقیقاً با جابجایی مخالف عمل کرده است بنابراین آن نقاط موازی با محور چرخش ترجمه می شوند. این نقاط روی محور موزی قرار دارند که از طریق آن می توان حرکت صلب را از طریق یک حرکت پیچ انجام داد.
[هندسه] $\vec{\omega}$
برای درک هندسه زیربنایی حرکت کلیدی است. منظور من از هندسه نقاط و خطوط کلیدی در فضا است که بینش حرکت را فراهم می کند. مفهوم محور چرخش چیزی است که من در اینجا در مورد آن صحبت می کنم.بنابراین چگونه$\vec{\omega}$ را تعریف میکنم براتون
? هر یک از سه جنبه فوق تعریف خاص خود را از حرکت چرخشی دارد و هر کدام در مورد یک چیز صحبت می کنند.
با استفاده از سینماتیک مشتق وکتورسوار بر یک فریم در حال چرخش را برای ایجاد قاعده کلی که
$\frac{{\rm d} \vec{A} }{{\rm d}t} = \frac{ \partial \vec{A}}{\partial t} + \vec{\omega} \times \vec{A}$که برای یافتن حرکات ذرات روی اجسام و استخراج معادله سینماتیکی که در بالا مشاهده شد استفاده میشح. این یک نوع استدلال دایرهایه زیرا مفهوم سرعت چرخش یک فریم فقط در آنجا پرتاب میشود و چون همه چیز جواب میدهد به این معنیه که حدس من درست بوده .
استفاده از میدان وکتور توصیف شده توسط نقاطی که حرکت می کننداما فاصله آنها را ثابت نگه می دارند همچنین به تعریف $\vec{\omega}$ منجر میشه
. ریاضی کمی پیچیدهتره اما فاصله بین دو نقطه A و B را به صورت $\ell_{AB} = \sqrt{ (\vec{r}_A - \vec{r}_B) \cdot ( \vec{r}_A - \vec{r}_B)}$در نظر بگیرید. و تمایز در طول زمان با قانون زنجیره ای چیزی شبیه به آن را به دست می دهد
$(\vec{r}_A - \vec{r}_B) \cdot ( \vec{v}_A - \vec{v}_B) = 0$که با حرکت نسبی چرخشی یا حرکت کاملاً انتقالی حل میشه. حرکت مطلق ترکیب این دو و در نتیجه قضیه Chasles.
با استفاده از هندسه می توانید نشان دهید که یک مکان از نقاط در فضا وجود دارد که یک خط بی نهایت را توصیف می کنه. در این خط حرکت ذرات جسم فقط موازی خطه. این تعریف محور چرخشه. این سرعت روی محور به صورت مضرب اسکالر وکتور چرخش $\vec{v}_{axis} = h\, \vec{\omega}$ تجزیه میشه
جایی که h گام نامیده میشه و نسبت سرعت انتقال به سرعت چرخشه. حرکت تمام ذرات روی یک جسم با موقعیت محور چرخش $\vec{r}$ توصیف میشه.
h و مقدار و جهت سرعت دورانی $\vec{\omega}$
$\vec{v} = h\,\vec{\omega} + \vec{r} \times \vec{\omega}$می توانید بین 3 مولفه سرعت و تجزیه هندسی $\vec{\omega}$ عقب و جلو بروید.
ابتدا تشخیص می دهید که با توجه به سرعت دورانی ω
یک جسم صلب و سرعت vA از یک نقطه خاص A می توانید سرعت هر نقطه دیگر B را بر اساس آن بیابید
$\boldsymbol{v}_B = \boldsymbol{v}_A + \boldsymbol{\omega} \times ( \boldsymbol{r}_B - \boldsymbol{r}_A )$جایی که rA
و rB بردارهای مکان هستند. و همینطور برای هر نقطه دیگری که بر روی جسم سفت و سخت سواره
بنابراین کل حرکت یک جسم صلب با سه جزء چرخشی ω مشخص میشه
و سه مولفه سرعت vA از هر نقطه دلخواه A. از این رو معمولاً میگم که یک جسم صلب دارای 6 درجه آزادیه
حال حالتی را در نظر بگیرین که جسم در حال چرخش حول مبدا هستش. علاوه بر این به موازات محور چرخش با v∥=hω حرکت می کند
. کمیت اسکالر h (به نام پیچ پیچ) نسبت سرعت انتقال به سرعت چرخشه. باز هم با آن می توانیم سرعت هر نقطه دیگری را مشخص کنم
$\boldsymbol{v}_A = h\,\boldsymbol{\omega} + \boldsymbol{\omega} \times \boldsymbol{r}_A$
در بالا بیان میشه که سه جزء vA را می توان با گام اسکالر h تشکیل داد
و دو جزء rA که با محور چرخش موازی نیستند. بنابراین با دانستن اینکه محور چرخش کجایه و گام آن چقدره حرکت جسم را می دانیم.
بخش جالب این که مشکل را برعکس کار کنید. با توجه به سرعت جسم در یک نقطه محور چرخش کجایه؟ در سیستم بالا vA داده شده
ما باید rA را بازیابی کنم و همچنین h .این کار به صورت زیر انجام میدم
$ h = \frac{ \boldsymbol{v}_A \cdot \boldsymbol{\omega} }{ \| \boldsymbol{\omega} \|^2} \\$
به طور خلاصه قضیه Chasle به ما این امکان را میده که هندسه حرکت را در هر موردی استخراج کنم اما مکان محور چرخش و همچنین گام پیچ را استخراج کنم. 6 درجه آزادی یک جسم صلب را می توان با $(\boldsymbol{\omega},\,\boldsymbol{v}_A)$ مشخص کرد. یا توسط
جهت محور چرخش $\boldsymbol{\hat{z}}$
(دو جزء)سرعت چرخش ω (یک جزء) به طوری که $\boldsymbol{\omega} = \omega \boldsymbol{\hat{z}}$
محل قرارگیری محور پیچ $\boldsymbol{r}_A$
(دو جزء)پیچ پیچ h (یک جزء)برای مجموع 6 درجه آزادی. تجزیه حرکت به صورت خلاصه میکنم
${\omega} = \omega \, (\boldsymbol{\hat{z}})$
جفت بالا $(\boldsymbol{\hat{z}}, \, h\,\boldsymbol{\hat{z}} + \boldsymbol{\hat{z}}\times \boldsymbol{r}_A)$
محور پیچ حرکت را در آنچه مختصات خط Plucker مینام مشخص کنم.اثبات
برای دریافت از (2) در (1) استفاده کنم
${v}_A = \frac{ (\boldsymbol{v}_A \cdot \boldsymbol{\omega}) }{ \| \boldsymbol{\omega} \|^2} \boldsymbol{\omega} + \boldsymbol{\omega} \times \frac{ (\boldsymbol{v}_A \times \boldsymbol{\omega}) }{ \| \boldsymbol{\omega} \|^2} $
سرعت زاویه ای نسبت به فریم های مختلف
: "به طور شهودی بدیهیه که زاویه چرخش یک جابجایی جسم صلب و همچنین وکتور سرعت زاویه ای لحظه ای مستقل از انتخاب مبدأ سیستم بدنه محوره متأسفانه به طور شهودی برای من واضح نیست.
معادله مربوطه برای محاسبه نرخ زمانی تغییر یک بوکتور بین یک فریم مرجع چرخان اینرسی و غیر اینرسی:
$\left(\frac{d\mathbf r}{dt}\right)_s = \left(\frac{d\mathbf r}{dt}\right)_r +\mathbf \omega\times\mathbf r$کجا s
نشان دهنده فضای ثابت فریم و r است
نشان دهنده فریم چرخانه.چگونه می توانم ω به عنوان مولفه های وکتور در یک فریم ثابت در فضابه طور کامل چرخش یک فریم چرخشی را که محور آن مثلاً در یک جسم صلب ثابته توصیف کنم؟ به نظر من انتخاب مبدا محور ثابت جسم نیز باید لحاظ شود و برای تعیین حرکت بعدی بسیار مهمه. مبدا تعیین می کند که محور چرخش از کدام نقطه (نقطه) عبور کند. اگر جسم صلب را حول نقطه مبدا P1 بچرخانم با تکانه زاویه ای ω1 حرکت مطمئناً متفاوت از چرخش حول نقطه مبدا P2 خواهد بود
همچنین با ω1 . من به اثبات این موضوع پرداختهام که چرا وکتور سرعت زاویهای در هر کدام از گزینههای مبدا جسم یکسانه اما همچنان سردرگم میمانم. تقریباً تنها چیزی که من می توانم با آن سازش کنم اینه که یک ω یکسانه
و دو مبدا جسم مختلف جهت چرخشی یک جسم صلب یکسان خواهد بو اما جسم بسیار متفاوت از مبدا محور ثابت در فضا منتقل میشه. با این حال این باعث میشود فکر کنم که جداسازی خوب حرکت انتقالی و چرخشی را که هنگام حل معادلات حرکت به دنبال آن هستیم پیچیدهتر میکند.
مرجع-فریم سرعت چرخش چرخشی-سینماتیکی زاویه ای-سرعت
معادله مربوطه برای محاسبه نرخ زمانی تغییر یک وکتور بین یک فریم مرجع چرخان اینرسی و غیر اینرسی:
$\left(\frac{d\boldsymbol r}{dt}\right)_s = \left(\frac{d\boldsymbol r}{dt}\right)_r +\boldsymbol \omega\times\boldsymbol r$کجا s
نشان دهنده فضای ثابت فریم و rهستش
نشان دهنده فریم چرخانه
این معادله مربوط به فریم اینرسی متحرک آنیه. در مورد یک اسپیس فریم غیر متحرک چطور؟ تعمیم این موضوع به فضایی که در آن منشا فریم چرخان در حال حرکته نتیجه میده $\left(\frac{d\boldsymbol r}{dt}\right)_s =
\left(\frac{d\boldsymbol r_0}{dt}\right)_s
+ \left(\frac{d(\boldsymbol r - \boldsymbol r_0)}{dt}\right)_r
+\boldsymbol \omega\times(\boldsymbol r - \boldsymbol r_0)$جایی که$\boldsymbol r_0$
وکتورجابجایی از مبدا فضای فریم به مبدأ فریم دواره.
فرض کنید از نقطه دیگری r1 استفاده می کنم که از دید فریم چرخشی ثابته (به عنوان مثال$\left(\frac{d(\boldsymbol r_1-\boldsymbol r_0)}{dt}\right)_r \equiv 0$
. ریاضی را مرور کنید (تمرینی که به شما واگذار می کنم) و آن را خواهید یافت
$\left(\frac{d\boldsymbol r}{dt}\right)_s =
\left(\frac{d\boldsymbol r_1}{dt}\right)_s
+ \left(\frac{d(\boldsymbol r - \boldsymbol r_1)}{dt}\right)_r
+\boldsymbol \omega\times(\boldsymbol r - \boldsymbol r_1)$به عبارت دیگرسرعت زاویه ای ω مستقل از انتخاب مبداهست
سرعت زاویه ای میله دوار
سیستم زیر را در نظر بگیرین
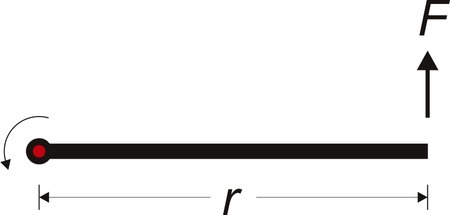
قانون دوم نیوتن برای حرکت چرخشی:
$\begin{equation}\tau=I\alpha \Leftrightarrow rF=\frac{1}{3}mr^{2}\alpha \Leftrightarrow \frac{d\omega}{dt}=\frac{3F}{mr}\end{equation}$با در نظر گرفتن ثابت RHS،$\omega=\frac{3F}{mr}t.$ بدست می آوریم.
من مطمئن نیستم که آیا سرعت زاویه ای با شعاع معکوس متناسب باشد یا نه (از تجربه طبیعی می دانم که هل دادن بیشتر به نیروی کمتری نیاز داره همچنین اگر میله ثابت نباشد و دو نیروی مخالف در انتهای میله عمل کنند چه اتفاقی می افتد.از آنجایی که مجموع آنها $\vec{0}$ است تعادل انتقالی وجود دارد و بنابراین محور چرخش در C.M است.
اما آیا عمل دو نیرو سرعت زاویه ای را نسبت به وضعیت قبلی تغییر میده
FBD موقعیت را در نظر بگیرید، جایی که نیروی واکنش R در زیر به معنای مثبت ترسیم شده است. همچنین مرکز جرم (نقطه آبی) که دقیقاً در $\tfrac{r}{2}$ قرار دارد نشان دادم
از محور.حالت A، بازوی محوری به این معنیه که شتاب خطی مرکز جرم با شتاب زاویه ای همراهه
$\ddot{y}_{\rm cm} = \tfrac{r}{2} \ddot{\theta}$
و دو معادله (خطی + زاویه ای) حرکت وجود داره
$\left. \begin{aligned} R + F & = m\, \ddot{y}_{\rm cm} \\ \tfrac{r}{2} F - \tfrac{r}{2} R & = I \ddot{\theta} \end{aligned} \;\right\}\; \begin{aligned} R & = \tfrac{F}{2} \\ \ddot{\theta} & = \tfrac{3 F}{m r} \end{aligned}$وقتی $I=\tfrac{m}{12} r^2$. پس بله، پوسیدگی. شتاب متناسب با r است از آنجایی که با وجود کمتر بودن بازوی ممان، گشتاور جرمی اینرسی به میزان $r^2$ کاهش می یابدمورد B، بازوی آزاد با R=−F برابر و مخالف روی انتهای میله اعمال می شود. همان معادلات حرکت، اما اکنون R شناخته شده است و شتاب خطی مشخص نیست. نتیجه این است
$\begin{aligned} \ddot{y}_{\rm cm} & =0 \\ \ddot{\theta} = \tfrac{r F}{I} & = \tfrac{12 F}{m r} \end{aligned}$دوباره پوسیدگی شتاب متناسب با r است به همین دلیل، اما کمیت با مورد A متفاوت است.
آیا سرعت زاویه ای یک میله دوار با تغییر محور چرخش آن تغییر می کند؟

اگر یک میله صلب به طول l با سرعت زاویه ای ω در یک سر به دور مبدا می چرخه و ناگهان انتهای ثابت در مبدا آزاد می شود و به میله اجازه میده تا آزادانه بدون هیچ نیروی خارجی روی آن حرکت کند سرعت زاویه ای جدید میله چقدر است؟ اکنون میله حول چه محوری می چرخد؟ من فکر می کنم که سرعت زاویه ای جدید همچنان ω باشد
اما اکنون در اطراف مرکز جرم میله خواهد بود. این حرکت زاویه ای را نسبت به مرکز جرم میله حفظ می کند و بزرگی سرعت مرکز جرم میله نیز بدون تغییر باقی می ماند (در نتیجه کل انرژی جنبشی میله حفظ می شود). آیا فکر من درست است یا حرکت زاویه ای تغییر می کند زیرا اکنون محور چرخش متفاوت است و ممان اینرسی میله نسبت به این محور چرخش جدید تغییر می کند؟
میله دقیقاً قبل از جدا شدن (بگذارید $t = -\epsilon$ را بزارم ) از مرکز چرخش (A) دارای سرعت زاویه ای ω است و تکانه زاویه ای L=Iω ، جایی که $v = \omega \frac{l}{2}$ درست پس از رها شدن میله، (بگذارید t=ϵ را فراخوانی کنم ) COM با سرعت ثابت $v_A = -\omega\frac{l}{2}$ در حال حرکت است ، زیرا این سرعت آن در$ t=−ε$ بودسرعت A در t=ε صفر است
. بنابراین سرعت نسبی آن نسبت به COM$v_A = -\omega\frac{l}{2}$ است
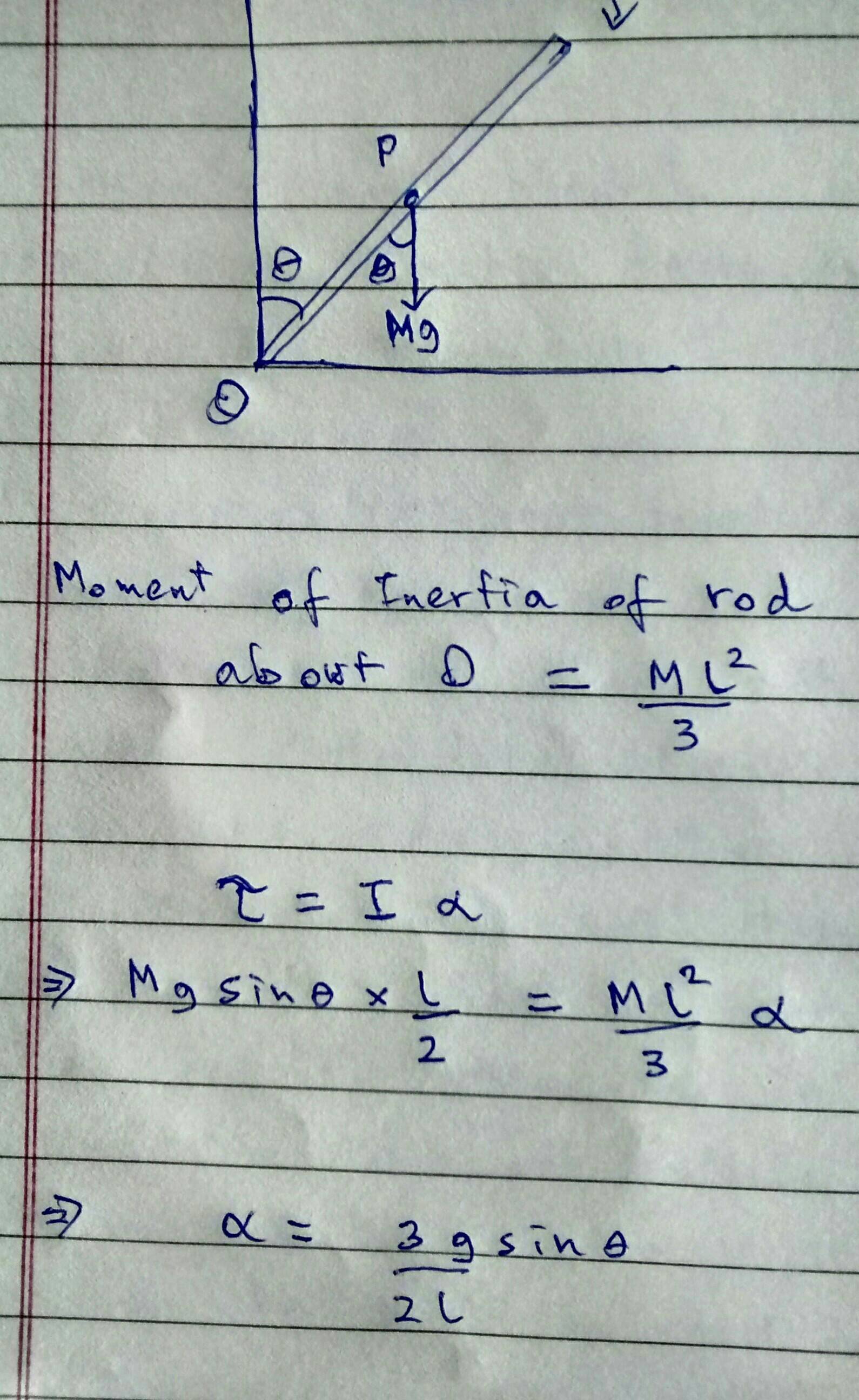
. سر مقابل میله دارای سرعت$v_B = \omega l$ است همزمان. سرعت زاویه ای جدید با توجه به COM است:
$\omega_1 = \frac{(\omega l - \omega\frac{l}{2})}{\frac{l}{2}} = \omega$تکانه زاویه ای جدید نسبت به A مجموع $\mathbf r \times \mathbf p_{COM}$ به علاوه حرکت زاویه ای اسپین با توجه به COM:
$L_1 = \frac{l}{2} m\omega \frac{l}{2} + I_1\omega$ممان اینرسی جدید نسبت به مرکز جرم $I_1 = \frac{ml^2}{12}$ است
بنابراین$L_1 = m\frac{l^2}{4}\omega + \frac{ml^2}{12}\omega = m\frac{l^2}{3}\omega = L$
انرژی جنبشی فقط چرخشی بود:
$E = \frac{1}{2}I\omega^2 = \frac{1}{2}m\frac{l^2}{3}\omega^2 = \frac{1}{6}ml^2\omega^2$
و بعداً انتقالی و چرخشی است:
$E_1 = \frac{1}{2}mv^2 + \frac{1}{2}I_1\omega^2 = \frac{1}{2}m(\omega \frac{l}{2})^2 + \frac{1}{2}(\frac{ml^2}{12})\omega^2 = \frac{1}{6}ml^2\omega^2 = E$
نکته مهم رهامی سیستم (میله) در ابتدا تحت تأثیر نیرویی است که توسط محور ایجاد می شود که باعث شتاب مرکز جرم میله می شود.
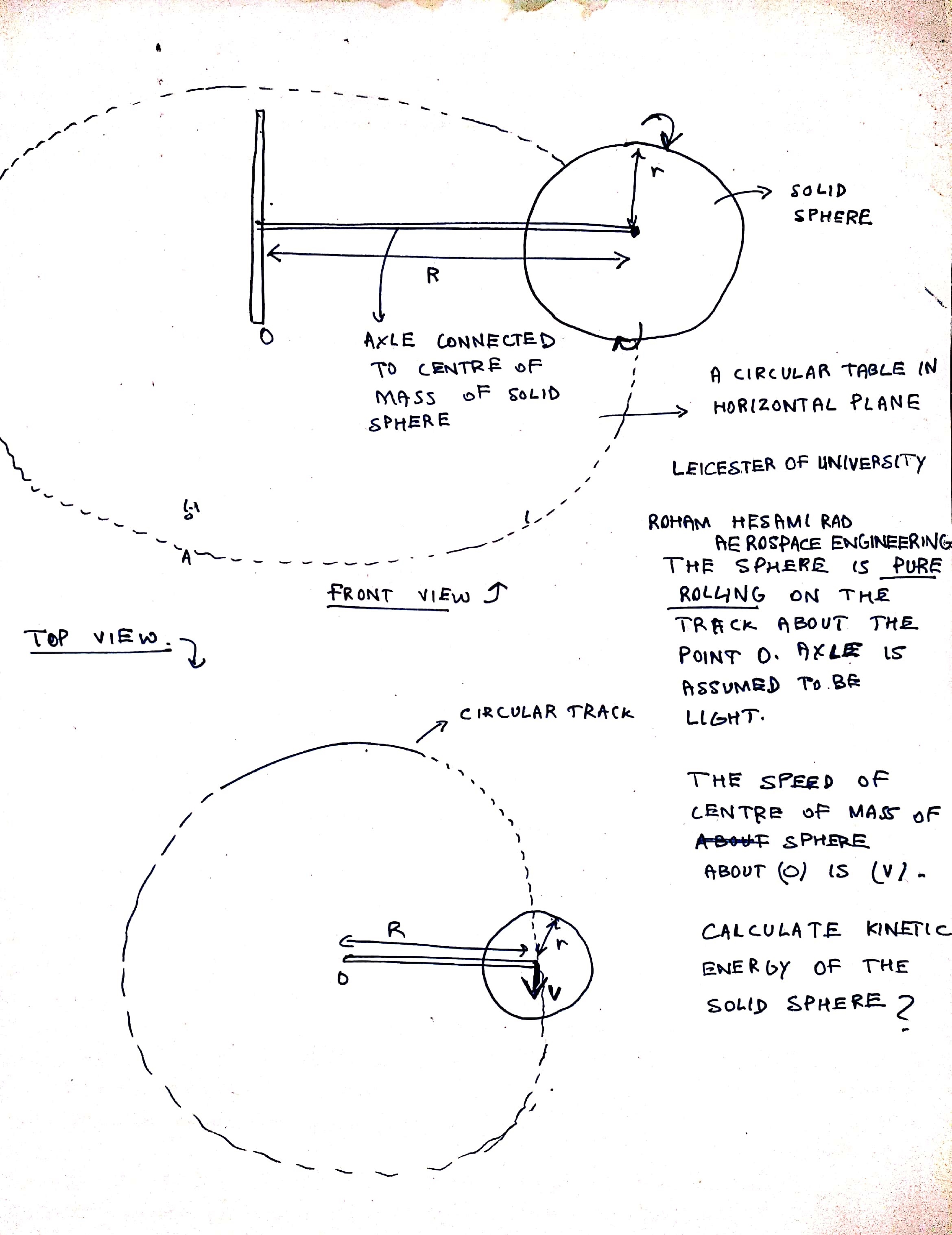
از آنجایی که خط عمل آن نیرو از مرکز جرم میله عبور می کند، گشتاوری روی سیستم وارد نمی شود و بنابراین تکانه زاویه ای آن ثابت است.
تکانه زاویه ای سیستم را می توان به دو صورت در نظر گرفت.
اولی به صورت$(I_{\rm G}+ml^2)\omega$ جایی که $I_{\rm G}+ml^2$ ممان اینرسی میله با جرم m است و طول$2l$ در مورد محور و ω سرعت زاویه ای آن است.
دومی به عنوان$I_{\rm G}\omega$ ، تکانه زاویه ای اسپین که مستقل از محور است، به اضافه $ml^2\omega$ تکانه زاویه ای مداری در مورد محور.توجه داشته باشید که مولفه مداری نیز برابر با $mlv$ است جایی که v سرعت خطی مرکز جرم است زیرا $v=l\omega$.اکنون محدودیتی را که به سیستم نیرو وارد می کند بردارید.اکنون مرکز جرم به صورت خطی با سرعت v حرکت می کند
در حالی که میله با سرعت زاویه ای ω می چرخد در مورد مرکز جرم آنتکانه زاویه ای در مورد نقطه محوری اصلی بدون تغییر خواهد بود، $I_{\rm G}\omega+mlv$
.اعمال قانون بقای انرژی در میله دوار
البته. پایستگی انرژی مستلزم آن است که مجموع انرژی جنبشی و پتانسیل ثابت بماند. انرژی پتانسیل ارتفاع مرکز جرم نسبت به یک نقطه دلخواه است. با انتخاب افقی بودن میله به عنوان آن نقطه دلخواه، انرژی پتانسیل به عنوان تابعی از$\theta$هستش $P = \frac 1 2 mgl \cos \theta$ است
. انرژی جنبشی از منظر یک قاب با مبدا در نقطه محوری کاملاً چرخشی است:$T = \frac12 \mathrm{I}\, {\dot\theta}^2$
جایی که $\mathrm I = \frac13 ml^2$
لحظه اینرسی یک میله باریک در یک سر است. با توجه به اینکه میله در ابتدا وقتی θ=0 حرکت نمی کند
، حفظ انرژی این امر را ایجاب می کند$\frac 1 2 mgl \cos \theta + \frac12 \frac13 ml^2\,{\dot\theta}^2 = \frac12 mgl$حل برای $\dot\theta$
جواب$2{\dot\theta}{\ddot\theta} = 3 \frac g l \sin\theta \dot\theta$تمایز با توجه به بازده زمانی
$2{\dot\theta}{\ddot\theta} = 3 \frac g l \sin\theta \dot\theta$یا $\ddot \theta = \frac 3 2 \frac g l \sin\theta$


