تعیین حداکثر و حداقل شتاب از v(t) مثال میگن$v(t) = 0.001302t^3 - 0.09029t^2 +23.61t - 3.083$ممشتق بگیر$a(t) = 3(0.001302)t^2 - 2(0.09029)t + 23.61$بنابراین اکنون می دانم که می توانم حداقل شتاب را در a′(t)=0 پیدا کنم
$a(t)=v'(t)=0.003906 t^2-0.18058 t+23.61$زمانی که $a'(t)=0\land a''(t)>0$، شتاب حداقل است
$a'(t)=0.007812 t-0.18058$
a′(t)=0 برای t0=23.1157
$a''(t)=0.007812>0$ بنابراین t0 حداقل محلی است به عنوان مشتق a(t) برای t>t0 مثبت است شتاب در حال افزایشه
علاوه بر این می توانیم مشاهده کنیم که a(t) معادله یک سهمی با تقعر به بالا ست،حداقل سرعت با استفاده از حساب دیفرانسیل و انتگرال
من سعی کرده ام به این سوال پاسخ دهم، که در آن $U = \frac{28\sqrt{15}}{15}$
و θ=53.3 درجه . برای بخش آخر باید حداقل مقدار v را تعیین کنم. به محض اینکه کلمه "حداقل" را دیدم، فکر کردم که باید از حساب دیفرانسیل و انتگرال برای حل آن استفاده کنم. من پاسخ کار به این را دیده ام اما حساب دیفرانسیل و انتگرال استفاده نمیشه حداقل مقدار v زمانی است که سرعت عمودی 0 باشد که من آن را درک می کنم. تلاش من برای این پاسخ درستی را به همراه نمی‌آورد که نمی‌دانم چرا از این رو فقط می‌توانم نتیجه بگیرم که چیزی در کاری که انجام می‌دهم اشتباه است.
روش من این بود که مقدار θ را پیدا کنم که برای آن v حداقل است. من این کار را با تشکیل یک معادله در v انجام دادم
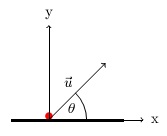
از معادله استاندارد حرکت v=u+at جایی که در مورد من:$v = usin(\theta) - gt$
پس $\frac{dv}{d\theta} = ucos(\theta) = 0$
سپس آنچه را که θ می دهد حل کنمم به عنوان $\frac{\pi}{2}$
سپس آن را به معادله اصلی خود وصل کردم تا مقدار v را به دست بیاورم که فکر می‌کردم حداقل است، اما به چیزی شبیه 12.37- رسیدم.
که نادرست است. اما پاسخ صحیح 4.32 متر بر ثانیه است.
خوب چگونه با استفاده از حساب دیفرانسیل و انتگرال پاسخ صحیح را استخراج کنم یا به من نشان دهد که کجا اشتباه کردم؟ من گمان می کنم که این معادله من از v باشد.
اگر از حساب دیفرانسیل و انتگرال استفاده کنم باید سرعت s را محاسبه کنم
، با توجه به زمان. یک بیت ماشه نشان می دهد که$s(t) = \sqrt{\text{verticalspeed}(t)^2 + \text{horizontalspeed}(t)^2}$
سرعت افقی ثابت است و سرعت عمودی را می توان با استفاده از v=u+at محاسبه کرد
.هنگامی که تمام مقادیر ثابت ها را پیدا کردید، می تونم s را متمایز کنم
و نقاط بحرانی را به صورت عادی پیدا کنم باید بگویم که رراه حل و روشθ به عنوان متغیر شما جایی است که اشتباه وارد شده است. θ در این مشکل رفع شده است، شما حتی ارزش آن را هم فهمیدید! متغیر مستقل شما باید زمان t باشد
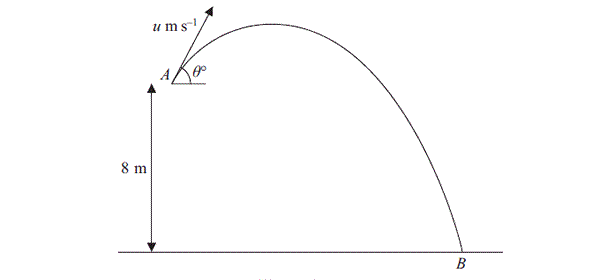
.معادله انرژی توسط$U = mgh + \tfrac{1}{2} mv^2$
پس به دست می آورم $mgh + \tfrac{1}{2} mu^2 = mg(h-8) + \tfrac{1}{2} m [2u]^2$
از کجا $3 u^2 = 16g$ ارتفاع توسط $h(t) = 8 + u_y t - \tfrac{1}{2} g t^2$
و h(2)=0 ، بدین ترتیب $u_y = g - 4$ مانند
$u^2 = u_x^2 + u_y^2$ برای نقطه B پیدا می کنم $u_x^2 = \frac{64}{3} g - [g-4]^2$
توجه داشته باشید که $\cos(\theta) = \frac{u_x}{u}$
بنابراین $\cos^2(\theta) = \frac{64 g - 3[g-4]^2}{16g}$حداقل سرعت $u_x$ است برای حرکت دایره ای عمودی، چرا حداقل سرعت برای یک چرخه کامل به چیزی که توپ به آن متصل است بستگی دارد؟
فرض کنید شرایط زیر را داریم و از من می‌خواهند حداقل سرعت را به توپ بدهند تا بتواند یک چرخه کامل را ادامه دهد.
اگر توپ با مقداری ماده سخت (مانند آهن) به نقطه وسط متصل شود، پاسخ این است: $v_{min}=\sqrt{4gh}$
(با استفاده از قانون بقای انرژی حداقل سرعت را محاسبه می کنیم تا توپ با سرعت صفر به اوج برسد و از آنجا یک چرخه کامل را ادامه دهد)
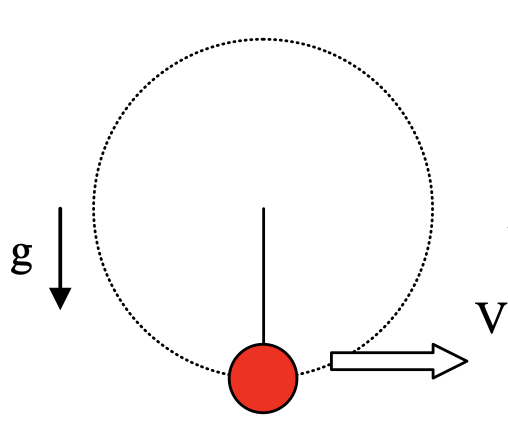اما اگر آهن را با یک طناب معمولی جایگزین کنیم، پس چرا پاسخ به$v_{min}=\sqrt{5gh}$ تغییر می کند.اگر توپ به یک تکیه گاه سخت متصل شود، در آن صورت محدود به حرکت در امتداد مسیر دایره ای است، بنابراین بدون توجه به سرعت، تا زمانی که غیر صفر باشد، حرکت دایره ای حاصل می شود.
در مقابل، اگر توپ به یک طناب غیر سفت وصل شود، این محدودیت دیگر معتبر نیست. اگر سرعت در بالای دایره به اندازه کافی بزرگ نباشد، گرانش توپ را از مسیر دایره ای پایین می کشد. توپ سقوط خواهد کرد این را با پشتیبانی سخت قبلی مقایسه کنید، جایی که حتی اگر سرعت کم باشد، میله توپ را پشتیبانی می کند و یک مسیر دایره ای همچنان امکان پذیر است.
اتخاذ روش کمی بیشتر، فقط در بالای دایره∗
، برای اینکه حرکت دایره ای رخ دهد به معادله زیر نیاز داریم:
$mg+F=\frac{mv^2}{R}$
جایی که m جرم توپ است، v سرعت توپ است، R شعاع دایره است و F نیرویی است که توسط تکیه گاه/طناب وارد می شود.
حال اگر سرعت آنقدر کم باشد که $mv^2/R<mg$ باشه ، پس برای اینکه این معادله معتبر باشه باید F<0 باشه ، یعنی نیروی ناشی از تکیه گاه به سمت خارج است. تکیه گاه سخت می تواند نیرویی به بیرون وارد کند، اما طناب نمی تواند (سعی کنید چیزی را با طناب هل دهید).
به همین دلیل است که بین حداقل سرعت اختلاف وجود دارد. برای پشتیبانی سخت F
می تواند به سمت بیرون اشاره کند و بنابراین v>0 در بالا کافی است با این حال، طناب نمی تواند توپ را به سمت بیرون هل دهد، بنابراین ما به$mv^2/R\geq mg$ نیاز داریم
این مفاهیم در سایر نقاط مسیر دایره ای نیز معتبر هستند، اما معادلات کمی پیچیده تر هستند. علاوه بر این، اگر توپ بتواند از بالای دایره عبور کند، با تقارن موقعیت، توپ آن را در امتداد دایره به پایین باز می‌گرداند. بنابراین، در اینجا فقط فکر کردن به بالای دایره کافی است.
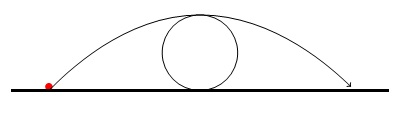
حداقل سرعت مورد نیاز برای پرش از روی جسم کروی که شعاع R و در فاصله d دارد چقدر است؟
حداقل سرعت اولیه ای که این ملخ برای پریدن از روی این کنده نیاز دارد چقدر است؟اقا ملخه میخوان بپرن کمکش کنیم
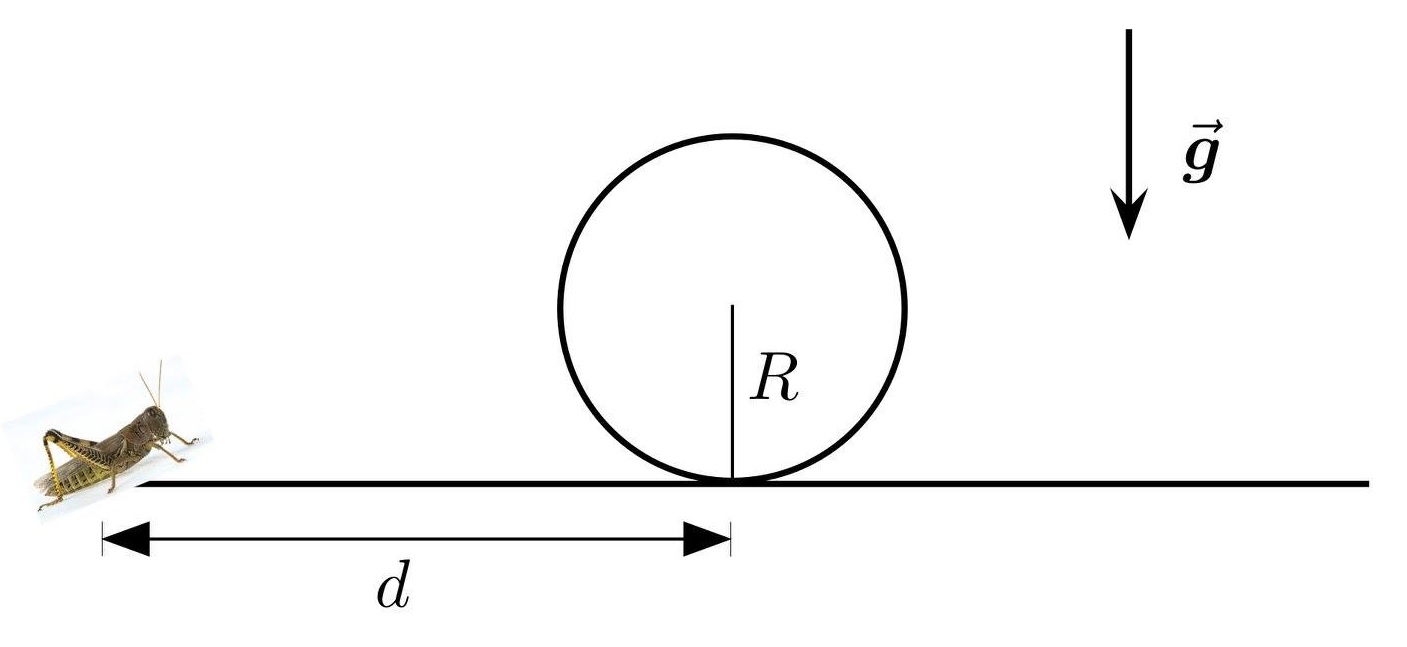
مسیر حرکت ملخ می تواند چوب را لمس کند اما نمی تواند از داخل کنده عبور کند.
d و R می توانند هر عدد حقیقی مثبتی باشند که d>R باشد. g یک شتاب گرانشی است (تقریباً 9.80665 m/s2 ).
فرض کنید توپ قرمز ملخ و در نقطه مبدا و y ارتفاع باشد
رابطه بین x و y برای حرکت پرتابه $y(x) = xtan\theta - \frac{gx^2}{2u^2cos^2\theta}$ است.
[/img] ، $0 < \theta < \frac{\pi}{2}$
منحنی بالایی کره را می توان در تابع توصیف کرد: $y_s(x) = R + \sqrt{R^2-(x-d)^2}$
، برای $d-R \leq x \leq d+R$
وضعیت کره $y(x) \geq y_s(x)$ است ، برای $d-R \leq x \leq d+R$
یا$xtan\theta - \frac{gx^2}{2u^2cos^2\theta} \geq R + \sqrt{R^2-(x-d)^2}$ ، برای $d-R \leq x \leq d+R$
در این مرحله، من نمی دانم چگونه $u_{min}(d,R)$را پیدا کنم
از این.(اگر مقدار d و h را بدهید (مثلاً d = 2m و R = 1m)، می توانید θ را پیدا کنید.
که شما را به حداقل می رساند.)
من فقط می دانم که y(x) (منحنی سهمی) برای ,$u_{min}(d,R)$
شبیه.حالت: d = cR (c یک ثابت است. نسبتی وجود دارد که باعث می شود y(x) دارای حداکثر نقطه در بالای کره باشد.)
مورد: d > cR
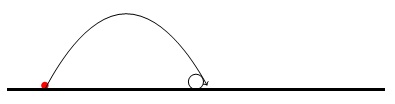
مورد: d <cR
این سوال جالبی است، اما من معتقدم که حل آن به صورت بسته غیرممکن است. با این حال، باید بتوانید مراحلی را که من می‌دهم دنبال کنید و یک راه‌حل گرافیکی/عددی دریافت کنید.
همانطور که می دانیم ملخ مسیر را دنبال می کند
$y = (\tan\theta)x - \frac12 g\big(\frac x{u\cos\theta}\big)^2.$ضریب لاگرانژ به ما می گوید که دایره $(x-d)^2+(y-R)^2=R^2$را قطع خواهد کرد.
به صورت مماس در یک نقطه (x,y) چه زمانی
$\left(\tan\theta - \frac{gx}{(u\cos\theta)^2}, -1\right) = \lambda(x-d,y-R)$برای برخی λ غیر صفر
. حذف λ معادله را به ما می دهد
$g(x,y,u,\theta) = x\Big(\frac1{y-R}-\frac g{(u\cos\theta)^2}\Big) - \frac d{y-R} + \tan\theta = 0.$تابع را در نظر بگیریم$F(x,y,u,\theta) = \big((x-d)^2+(y-R)^2-R^2,g(x,y,u,\theta)\big)$نقشه برداری یک منطقه مناسب در $\Bbb R^4$
به $\Bbb R^2$. من به مجموعه صفر علاقه مندم $F(x,y,u,\theta) = (0,0)$
.قضیه تابع ضمنی به ما می گوید که اگر 2×2 از ژاکوبین f داده شده توسط $\frac{\partial F}{\partial (x,y)}$ غیر صفر است، پس در آن مجموعه صفر می توانیم به صورت محلی برای (x,y) حل کنیم.
به عنوان توابع (u,θ) در یک مجموعه باز از آنجایی که من به دنبال حداقل u ممکن هستیم
، من نمی تونم اجازه دهم
کوچکتر شود، و از این رو چنین راه حل محلی در یک مجموعه باز وجود ندارد. بنابراین باید $\frac{\partial F}{\partial (x,y)} = 0$داشته باشیم
. انجام این کار و جایگزینی معادله $(x-d)^2+(y-R)^2=R^2$
جایی که مناسب است باید دریافت کنیم
$R^2(u\cos\theta)^2 = g(y-R)^3$اکنون y=y(u,θ) داریم
. جایگزینی $g(x,y,u,\theta)=0$
فرمول x را می دهد
به عنوان تابع (u,θ)
. با استفاده از معادله$(x-d)^2+(y-R)^2=R^2$
یک بار دیگر، بالاخره معادله $h(u,\theta) = 0$را به دست خواهیم آورد
.یک بار دیگر به قضیه تابع ضمنی متوسل می شویم. اگر $\dfrac{\partial h}{\partial \theta}\ne 0$، مانند قبل، θ را دریافت خواهیم کرد
به صورت محلی به عنوان تابعی از u در یک فاصله باز از u ارزش های. از آنجایی که زمانی که ما حداقل u را پیدا کرده ایم، این نیز نمی تواند اتفاق بیفتد
، ما باید$\frac{\partial h}{\partial \theta} = 0.$جایگزین کردن مقادیر x(u,θ)
و y(u,θ) در این حداقل باید معادله ای ارائه شود که بتوان آن را حل کرد تا حداقل u را بدست آورد
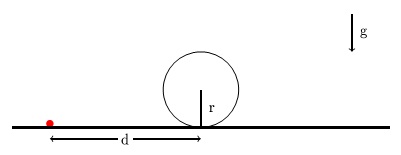
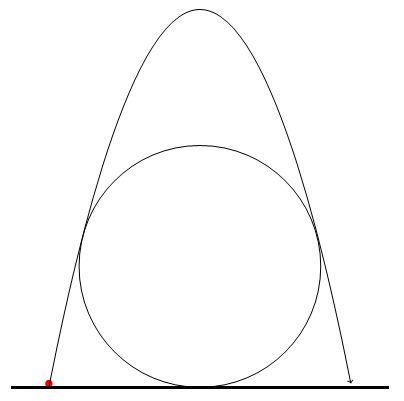
.برای R<d≤2R
و تماس متقارن (دو نقطه تماس، در دو طرف دایره)
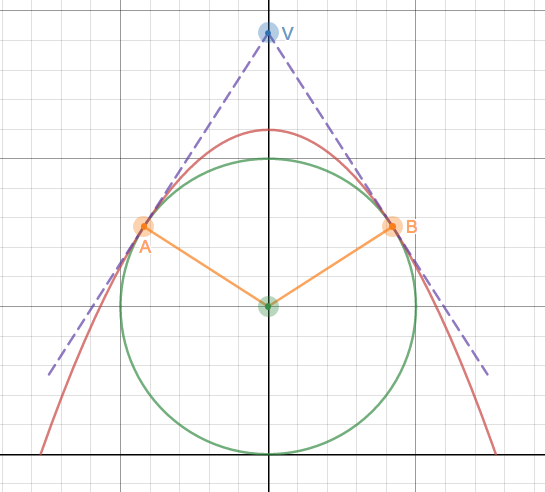
]موردی را در نظر بگیرید که سهمی (مسیر پرتابه) دایره (مقطع کره) را در دو نقطه A,B لمس کند.
. بگذارید این نقاط زاویه θ را کاهش دهند
به سمت عمودی در مرکز دایره.
نقطه تماس بین دایره و زمین را به عنوان مبدا در نظر بگیرید.
اجازه دهید V(0,h) نقطه تقاطع مماس ها (هم به مسیر و هم به دایره) در A,B باشد
. با مثلثات ساده می توان به راحتی دریافت که $h=R\left(1+\frac 1{\cos\theta}\right)$
از این
$A\big(-R\sin\theta, R(1+\cos\theta)\big); \qquad V\big(0,R\left(1+\tfrac 1{\cos\theta}\right)\big); \qquad
B\big(R\sin\theta, R(1+\cos\theta)\big)$از این رو شکل پارامتری سهمی را می توان به صورت منحنی بزیه درجه دوم به صورت زیر بیان کرد:
$\begin{align}
(x,y)
&=\bigg(t^2(-R\sin\theta+2t(1-t)\cdot 0+(1-t)^2(R\sin\theta)\; ,\\
&\qquad t^2 R(1+\cos\theta)+2t(1-t)R(1+\tfrac 1{\cos\theta})+(1-t)^2R(1+\cos\theta) \bigg)\\
&=\bigg(\ (1-2t)R\sin\theta\; ,\;(1-2t+2t^2)R(1+\cos\theta)+2t(1-t)R(1+\tfrac 1{\cos\theta})\ \bigg)\end{align}$حذف t
شکل دکارتی مسیر را می دهد
$\boxed{y=\frac {R^2(1+\cos\theta)^2-x^2}{2R\cos\theta}}\\
\text{which is equivalent to }\\
\boxed{\frac {x^2}{R^2(1+\cos\theta)^2}+\frac y{\left(\frac {R^2(1+\cos\theta)^2}{2R\cos\theta}\right)}=1}$که معادل $\boxed{y=\frac {R^2(1+\cos\theta)^2-x^2}{2R\cos\theta}}\\
\text{which is equivalent to }\\
\boxed{\frac {x^2}{R^2(1+\cos\theta)^2}+\frac y{\left(\frac {R^2(1+\cos\theta)^2}{2R\cos\theta}\right)}=1}$است
همانطور که نقطه پرتاب به صورت $(-d,0)$ داده می شود
، این می دهد
$d=R(1+\cos\theta)\Longrightarrow \cos\theta=\tfrac dR-1$از این رو معادله مسیر تبدیل می شود
$\boxed{y=\frac {d^2-x^2}{2(d-R)}}\\
\scriptsize(R<d\le 2R)\\
\text{which is equivalent to}\\
\boxed{\frac {x^2}{d^2}+\frac y{\left(\frac{d^2}{2(d-R)}\right)}=1}\\
\frac {dy}{dx}=-\frac x{d-R}=\frac d{d-R}\text{ at } x=-d$که معادل $\boxed{y=\frac {d^2-x^2}{2(d-R)}}\\
\scriptsize(R<d\le 2R)\\
\text{which is equivalent to}\\
\boxed{\frac {x^2}{d^2}+\frac y{\left(\frac{d^2}{2(d-R)}\right)}=1}\\
\frac {dy}{dx}=-\frac x{d-R}=\frac d{d-R}\text{ at } x=-d$در x=−d است
اجازه دهید v،α
به ترتیب سرعت پرتاب و زاویه پرتاب باشد.
از این رو
$\boxed{\tan\alpha =\frac d{d-R}}$
معادل سازی ضرایب $x^2$ با معادله خط سیر استاندارد )$y=x\tan\alpha-\frac {gx^2}{2v^2}(1+\tan^2\alpha)$
میده
.$\color{red}{v^2}\color{red}{=gd\left(\frac d{d-R}+\frac {d-R}d\right)}
$
ارتفاع پرش:
$2R = \frac{\dot y_0^2}{2g}$بنابراین:
$\dot y_0 = \sqrt{Rg}$حالا هر جزء را جداگانه بگیرم. ابتدا حداقل سرعت عمودی مورد نیاز برای پرش از ارتفاع 2R چقدر است؟ همانطور که در اوج به 2R می رسد و شروع به سقوط می کند. بنابراین، سرعت او در ارتفاع 2R صفر خواهد بود. از معادله استفاده میکنم
$\dot y_{2R} = 0 = \dot y_0 - gt$
این زمان رسیدن به ارتفاع 2R در گرانش است. خوب، اقاملخه باید $d = \dot x t$طی کنه
در این زمان بنابراین:
$t = \frac{d}{\dot x}$حل کردن برای $\dot y_0$
و ˙$\dot x$
و جایگزین کردن t در صورت مناسب بودن بازده:
$\dot y_0 = t \cdot g = \frac{d \cdot g}{\dot x}$
$\dot x =\frac{d}{t} = \frac{d \cdot g}{\dot y_0}$
جایگزین $\dot y_0$
از بالا:
$\dot x = \frac{d \cdot g}{\sqrt{Rg}}$بقیه به خودمم مربوطه. من دو جزء خود را بر حسب R دارم، g، و d
.حداقل سرعت اولیه →
حداقل انرژی جنبشی در شروع $E=1/2mv^2=1/2m({v_h}^2+{v_v}^2=E_h+E_v$
حداقل انرژی جنبشی عمودی در شروع Ev
(سرعت و انرژی ترجمه افقی تحت تأثیر قرار نمی گیرند) حداقل انرژی پتانسیل در بالا حداقل h
.با توجه به راس و یک نقطه (شروع)، سهمی کاملاً تعیین می شود: بنابراین حداقل h
مربوط به سهمی مماس بر دایره داده شده است.
برای ساده کردن محاسبات، اجازه دهید نمایش را مانند قسمت دوم طرح بالا معکوس کنیم، و سهمی$y=ax^2$ا در نظر بگیریم.
.یک دایره به صورت دو مماس به سهمی خواهد بود اگر مرکز آن روی محور و در حالت عادی به سهمی باشد.
مماس بر سهمی در یک نقطه $(x_0,a{x_0}^2)$
دارای شیب $2a{x_0}$
، بنابراین شیب نرمال $-1/(2a{x_0})$ است.
.بنابراین اگر تحمیل کنیم که مرکز در (0,h) باشد
، در حالت عادی و در فاصله R
از سهمی، می گیریم
$\left\{ \matrix{
{{h - a\,x_{\,0} ^{\,2} } \over {x_{\,0} }} = {1 \over {2\,a\,x_{\,0} }} \hfill \cr
\left( {h - a\,x_{\,0} ^{\,2} } \right)^{\,2} + x_{\,0} ^{\,2} = R^{\,2} \hfill \cr} \right.\quad \Rightarrow \quad \left\{ \matrix{
h = a\,R^{\,2} + {1 \over {4\,a}} \hfill \cr
x_{\,0} ^{\,2} = R^{\,2} - {1 \over {4\,a^{\,2} }} \hfill \cr} \right.$که می گوید دایره دو مماس شعاع R
مرکز آن$h=1/(4a)+aR^2$ است
.پس از آن سهمی از نقطه شروع عبور می کند $(-d, R+h)$، و حل برای a
$\eqalign{
& \left\{ \matrix{
h = {1 \over {4\,a}} + a\,R^{\,2} \hfill \cr
R + h = a\,d^{\,2} \hfill \cr} \right.\quad \Rightarrow \quad \left\{ \matrix{
4R^{\,2} \,a^{\,2} - 4\,ah + \,1 = 0 \hfill \cr
R + h = a\,d^{\,2} \hfill \cr} \right.\quad \Rightarrow \cr
& \Rightarrow \quad \left\{ \matrix{
4R^{\,2} \,a^{\,2} - 4\,ah + \,1 = 0 \hfill \cr
h = a\,d^{\,2} - R \hfill \cr} \right.\quad \Rightarrow \cr
& \Rightarrow \quad \left( {d^{\,2} - R^{\,2} } \right)\,a^{\,2} - \,R\,a - \,1/4 = 0 \cr}$که به معنی
$\eqalign{
& a = {{R \pm \sqrt {R^{\,2} + \left( {d^{\,2} - R^{\,2} } \right)} } \over {2\left( {d^{\,2} - R^{\,2} } \right)}}\, = {{R \pm d} \over {2\left( {d^{\,2} - R^{\,2} } \right)}} = \cr
& = {{R \pm d} \over {2\left( {d + R} \right)\left( {d - R} \right)}} = \left\{ \matrix{
{1 \over {2\left( {d - R} \right)}} \hfill \cr
- {1 \over {2\left( {d + R} \right)}} \hfill \cr} \right. \cr}$ما علاقه مند به راه حل مثبت هستیم، بنابراین نتیجه نهایی است
.جایی که :اگر d→R
، سپس به وضوح h و a به بی نهایت بروید در حالی که x0
R می شود اگر d→2R ، سپس دایره دارای شعاع R=1/(2a) است.
برابر با انحنای راس سهمی، h
R می شود و اگر d بیش از 2R افزایش می یابد
.و البته، هنگامی که پارامترهای سهمی را تعریف کردید (و به طرح اصلی برگردانید)، ارزیابی حداقل سرعت اولیه و زاویه ارتفاع آسان است.
من فکر می کنم که ساده ترین راه این است که فقط "تغییر" g
و سپس در نظر بگیرید که سرعت عمودی باید مثبت در نظر گرفته شود.
بنابراین، با نشان دادن T
زمان رسیدن به بالا (پایین)، توسط u
و v
سرعت افقی و عمودی را خواهیم داشت
$\left\{ \matrix{
u\,T = d \hfill \cr
g\,T = v \hfill \cr
{{g\,T^2 } \over 2} = R + h = a\,d^{\,2} = {{d^{\,2} } \over {2\left( {d - R} \right)}} \hfill \cr} \right.$و در نهایت، همیشه برای R≤d≤2R
، تمام پارامترهای مورد نیاز به راحتی به دست می آیند:
$\bbox[lightyellow] {
\left\{ \matrix{
a = {1 \over {2\left( {d - R} \right)}} \hfill \cr
R + h = {{d^{\,2} } \over {2\left( {d - R} \right)}} \hfill \cr
T = {d \over {\sqrt {g\left( {d - R} \right)} }} \hfill \cr
u\, = \sqrt {g\left( {d - R} \right)} \hfill \cr
v = {{g\,d} \over {\sqrt {g\left( {d - R} \right)} }} \hfill \cr
\tan \theta = {v \over u} = {{\,d} \over {\left( {d - R} \right)}} \hfill \cr
u^{\,2} + v^{\,2} = g\left( {2d + {{\,R^{\,2} } \over {\left( {d - R} \right)}}} \right) \hfill \cr} \right.
}$که معادله پارامتری را در زمان به عنوان نشان می دهد
$\bbox[lightyellow] {
\left\{ \matrix{
y(t) = R + h - {1 \over 2}g\left( {t - T} \right)^2 = d\sqrt {{g \over {d - R}}} \;t - {1 \over 2}g\,t^2 \hfill \cr
x = u(t - T) = - d + \sqrt {g\left( {d - R} \right)} \;t \hfill \cr} \right.
}$که در واقع تبدیل می شود
$\bbox[lightyellow] {
y(x) = R + h - {1 \over 2}g\left( {{x \over u}} \right)^2 = R + h - a\,x^2 = {{d^2 - x^2 } \over {2\left( {d - R} \right)}}
}$
$y = R+h - a(x-d)^2$
$y = R+h - ax^2 + 2axd - ad^2$
$y = 2axd - ax^2$
$y(x) = x\tan\theta - \frac{gx^2}{2u^2cos^2\theta}$
$\tan\theta = 2ad$
$\cos\theta = \frac{1}{\sqrt{(2ad)^2+1}}$
$a = \frac{g}{2u^2cos^2\theta} = \frac{g((2ad)^2+1)}{2u^2}$
$u^2 = \frac{g((2ad)^2+1)}{2a}$
$u^2 = g(d-R)((\frac{d}{d-R})^2+1)$
$u^2 = g(d-R)((\frac{d}{d-R})^2+1)$
$u = \sqrt{\frac{g(d^2+(d-R)^2)}{d-R}}$
