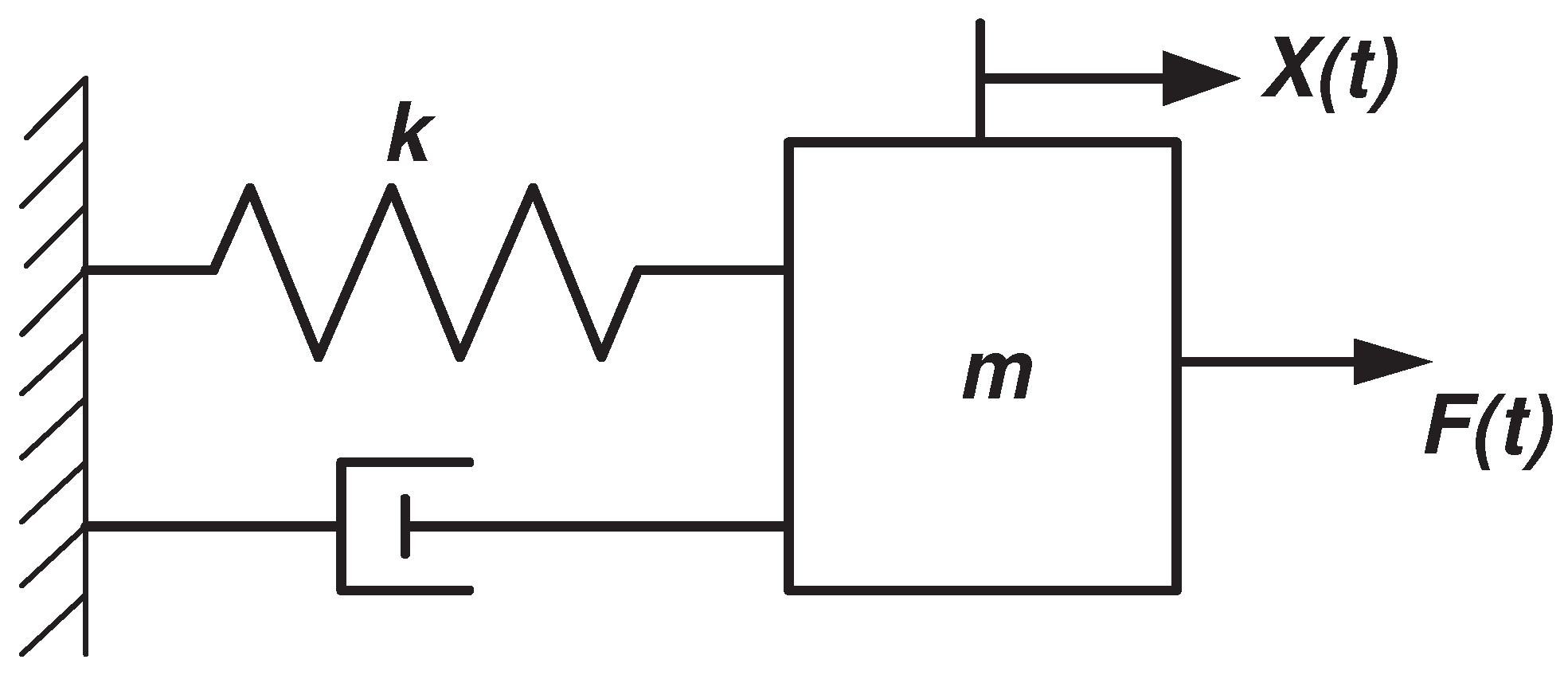
میتوانیم میرایی بحرانی را از معادله حرکت محاسبه کنیم:
$mx_{tt} + cx_t + kx = 0$
$ms^2 + cs + k = 0$
$s= \frac{-c ± \sqrt{c^2-4mk}}{2m}$
سپس سه شرط وجود دارد:
$c^2 <4mk$ (تحت میرایی)
$c^2 >4mk$ (بیش از میرایی)
$c^2 =4mk$ (میرایی بحرانی)
سپس نسبت میرایی با$\frac{c}{\sqrt{4mk}}$ بیان می شود
.سوال
من نمی دانم که آیا یا چگونه می توان این را به سیستم های پیچیده تر گسترش داد.
فرض کنید یک فنر دوم را به سیستم موازی اضافه کنید:
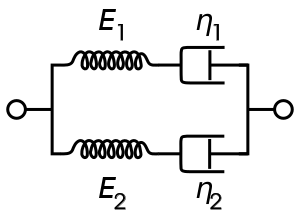
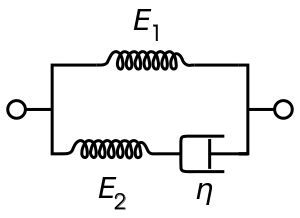
این یک مدل ویسکوالاستیک است که در آن رابطه سازنده بر حسب تنش (σ) و کرنش (Ɛ) است:
$σ = E_1Ɛ + \frac{η(E_1+E_2)}{E_2}\dot{Ɛ} - \frac{η}{E_2}\dot{σ}$
آیا می توان میرایی بحرانی یا نسبت میرایی را به همین ترتیب محاسبه کنم؟ اگر چنین است چگونه کار می کنه؟
با دو فنر و دو دمپر اینجوری چطور؟

$σ = (η_1+η_2)\dot{ϵ} + \frac{η_1η_2(E_1+E_2)}{E_1E_2} - (\frac{η_1}{E_1} + \frac{η_2}{E_2})\dot{σ} - \frac{η_1η_2}{E_1E_2}\ddot{σ}$
آیا می توان همین کار را انجام بدم و اگر ممکنه چگونه؟
حدس من
حدس من این است که کرنش معادل x است و تنش برابر با نیرو است، بنابراین می توانیم سیستم 3 عنصری را بازنویسی کنیم:
$0 = E_1Ɛ + \frac{η(E_1+E_2)}{E_2}\dot{Ɛ} - \frac{η}{E_2}\dot{σ} - σ$
$0 = E_1x + \frac{η(E_1+E_2)}{E_2}\dot{x} - m\frac{η}{E_2}\dddot{x} - m\ddot{x}$
$0 = E_1 + \frac{η(E_1+E_2)}{E_2}s - ms^2 - m\frac{η}{E_2}s^3$
ریشه های زیر را می دهد:
$s = \frac{-E_1E_2}{η(E_1+E_2)}$
$s = ±\sqrt{\frac{E_1}{m}}$
اما این برای حل هر سناریوی میرایی بحرانی که بتوانم آن را بفهمم مفید نیست.
آیا روش دیگری وجود دارد یا من چه چیزی را خراب کردم؟
هر گونه کمک یا راهنمایی قدردانی می شود.
همانطور که می توانید مقاومت ها را در مدارهای الکتریکی به صورت سری یا موازی با یک مقاومت معادل جایگزین کنم، ما می تونم همین کار را با فنرها و دمپرها انجام دهم و می تونم آنها را با یک فنر و دمپر به صورت موازی جایگزین کم
بیایید سیستم زیر را در نظر بگیریم:
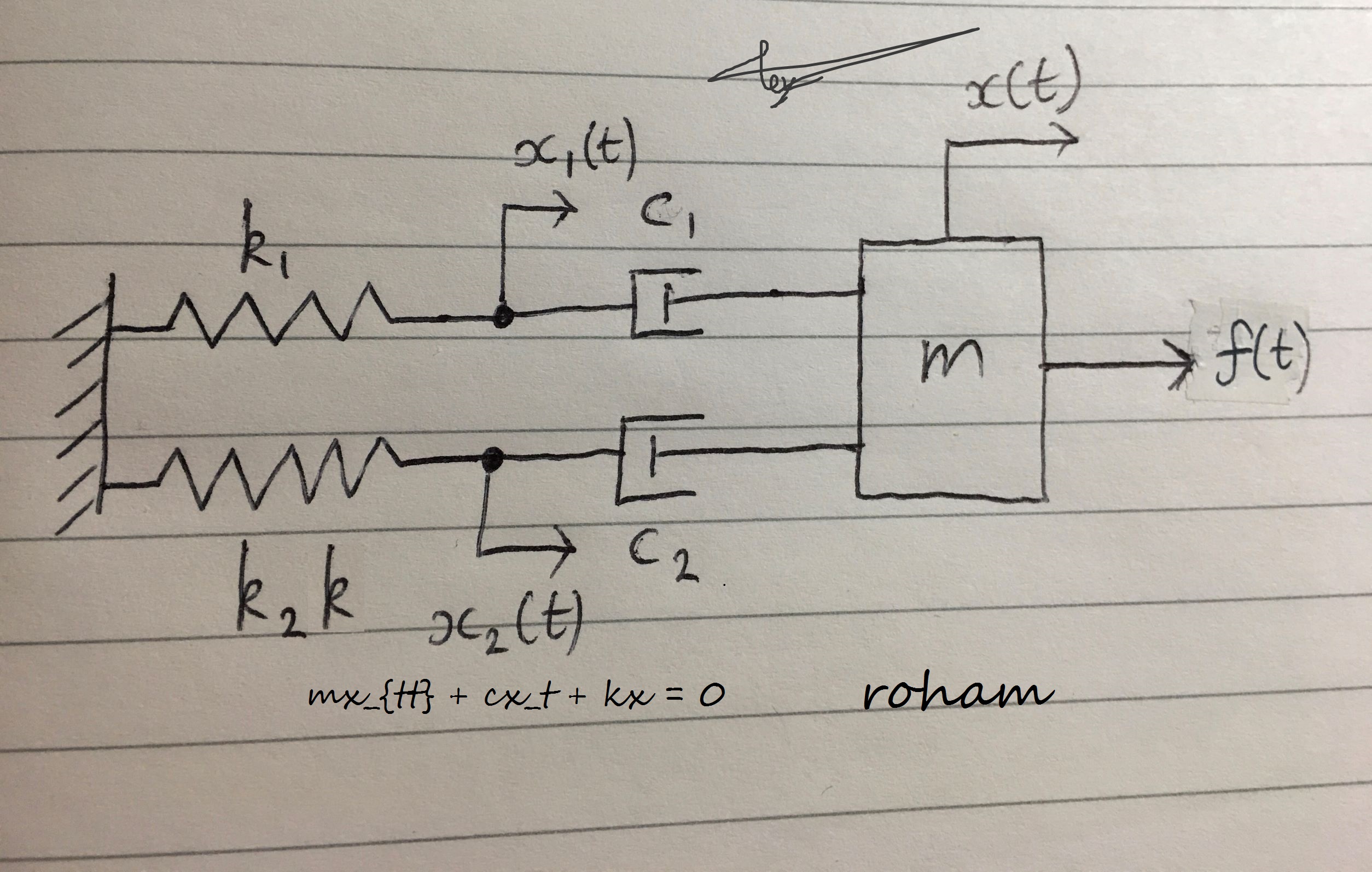
توج داشته باشید که گره های بین هر فنر و دمپر دارای برچسب جابجایی هستند. ما می توانیم این سیستم را به پنج نمودار جسم آزادFBD تقسیم کنم:
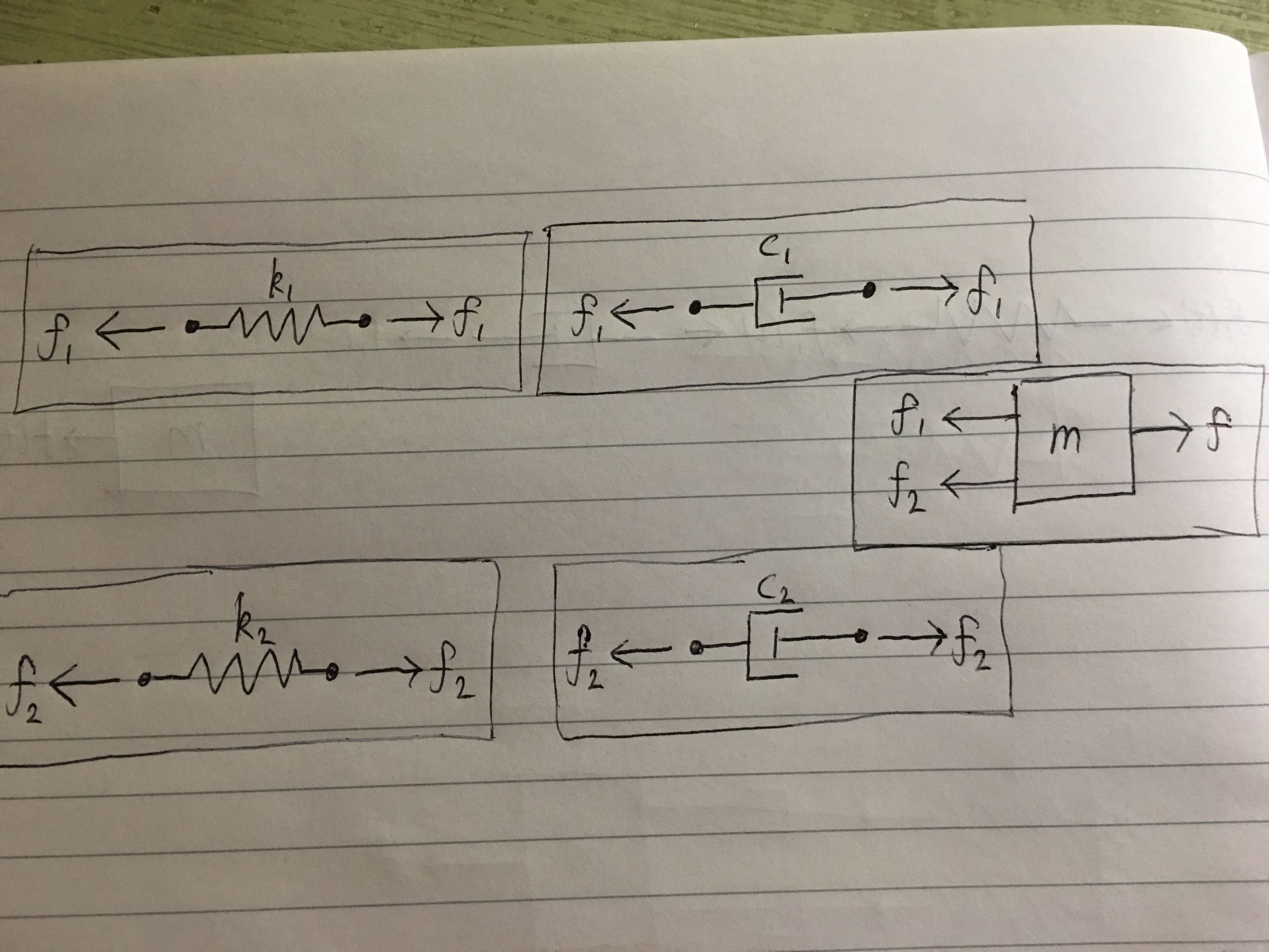
توجه داشته باشید که چگونه نیرو از طریق هر شاخه یکسان است، زیرا در هر شاخه جرمی وجود ندارد. اکنون می تونم معادلاتی را برای هر نمودار جسم آزاد بیان کنم
در حال حاضر، اجازه دهید دو نمودار جسم آزاد در شاخه بالایی را در نظر بگیرم. معادلات را رعایت می کنند
$f_1 = k_1 x_1$
و$f_1 = c_1 (\dot{x}-\dot{x}_1)$
به ترتیب.حال، بیایید از خطی بودن سیستم استفاده کنم و فرض کنم همه جابجایی ها و نیروها به صورت سینوسی در فرکانس ω تغییر می کنند.
:$f_1(t) = \hat{f}_1 \, \mathrm{e}^{\mathrm{i}\omega t}, \qquad x_1(t) = \hat{x}_1 \, \mathrm{e}^{\mathrm{i}\omega t}, \qquad \mathrm{etc...}$
جایگزینی این عبارات در دو معادله به ما نتیجه می دهد
$\hat{f}_1 = k_1 \hat{x}_1$
$\hat{f}_1 = \mathrm{i}\omega c_1 (\hat{x}-\hat{x}_1)$
(به طور معادل، ما می توانستیم تبدیل فوریه معادلات را بگیریم) توجه کنید که چگونه دومی از معادلات f=kx یکسان است.
شکل فنر یعنی یک دمپر معادل یک فنر با سفتی خیالی و وابسته به فرکانس $\mathrm{i} \omega c_1$ است.
.و می توانیم فنر و دمپر را در شاخه با هم ترکیب کنم که انگار دو فنر هستند. با حذف $\hat{x_1}$
، که در ابتدا جابه جایی نبود که ما واقعاً به آن اهمیت می دادیم، معادله را دریافت می کنم
$\hat{f}_1 = \left(\frac{1}{\mathrm{i}\omega c_1} + \frac{1}{k_1}\right)^{-1} \hat{x}$
یا فشرده تر،
$\hat{f}_1 = k_1^*(\omega) \hat{x}$
یعنی ما با موفقیت فنر و دمپر را در یک شاخه با یک فنر با سختی پیچیده جایگزین کردم، جایی که k∗1(ω)
سختی پیچیده است. توجه داشته باشید که چگونه قانون ترکیب دو فنر به صورت سری معادل قانون ترکیب دو مقاومت به صورت موازی است.
می توانیم این کار را برای شاخه پایین تکرار کنم تا به دست آید
$\hat{f}_2 = k_2^*(\omega) \hat{x}$
ممن اکنون سیستم خود را به داشتن دو فنر پیچیده به صورت موازی کاهش دادم. فنر موازی را می توان به یک فنر منفرد ترکیب کرد که سفتی آن مجموع فنرهای منفرد است. بنابراین، اکنون سیستم خود را به موارد زیر کاهش دادم:
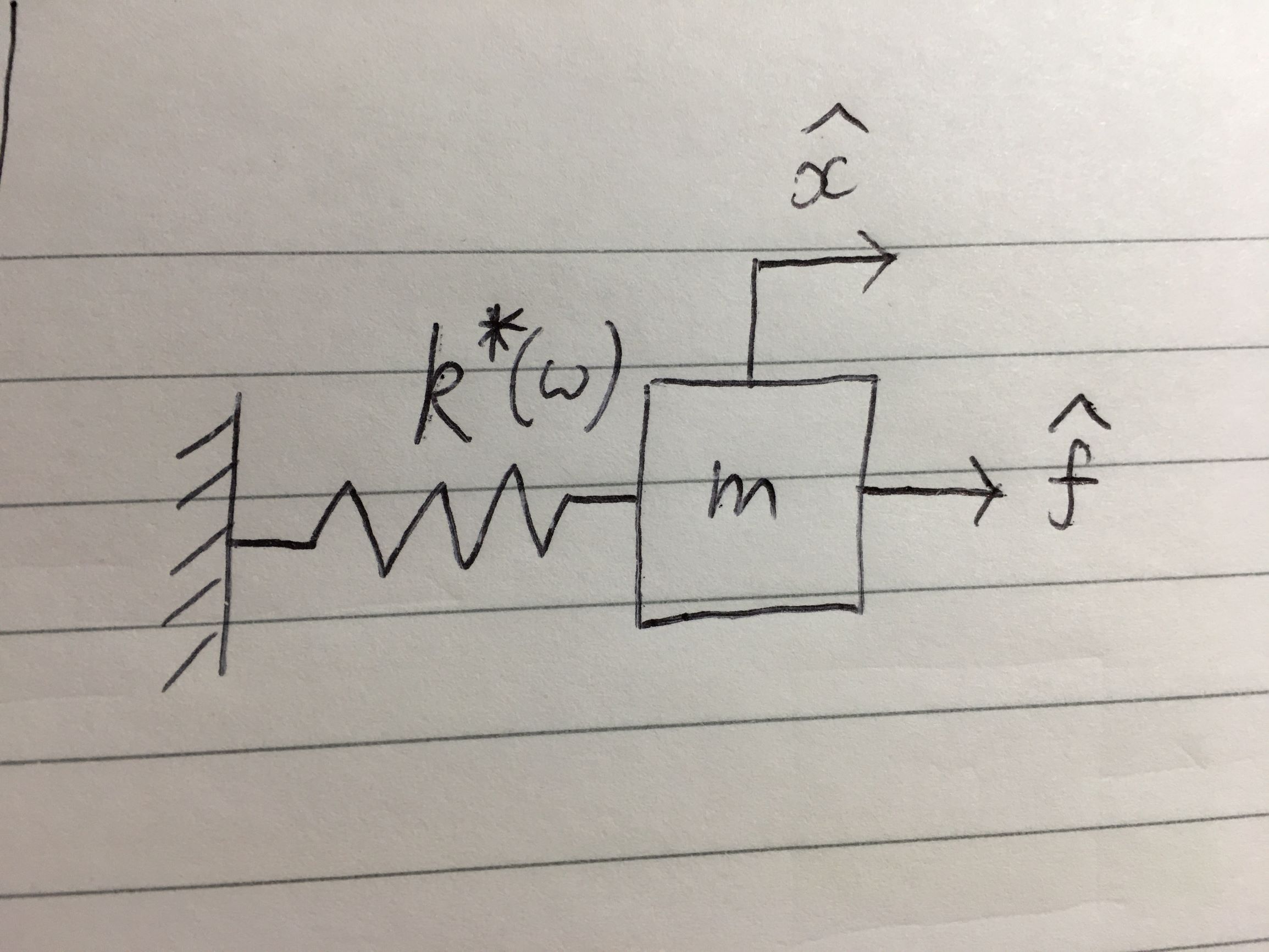
که در آن سختی مختلط معادل$k^*(\omega)$ است$k^*(\omega) = \frac{k_1 \mathrm{i}\omega c_1}{k_1+ \mathrm{i}\omega c_1} + \frac{k_2 \mathrm{i}\omega c_2}{k_2+ \mathrm{i}\omega c_2}$
سیستم معادل ما، به یاد می آورد که حرکت رخ داده در فرکانس ω سینوسی است
، از معادله زیر پیروی می کند:
$-\omega^2 m \hat{x} + k^*(\omega)\hat{x} = \hat{f}$
اگر بخواهیم کارها را در حوزه لاپلاس به جای دامنه فوریه انجام دهیم، معادله سیستم شبیه (iω→s
)$\left(s^2 m + \frac{k_1 s c_1}{k_1+ sc_1} + \frac{k_2 s c_2}{k_2+ sc_2}\right) X(s) = F(s)$
اکنون، این جایی است که من کمتر مطمئن هستم، اما حدس من (در مقایسه با آنچه شما برای مورد ساده تر انجام دادید) این است که معادله را در نظر بگیرم.
$s^2 m + \frac{k_1 s c_1}{k_1+ sc_1} + \frac{k_2 s c_2}{k_2+ sc_2} = 0$
که می تواند دوباره به صورت یک معادله مکعب بیان شود. (این معادله را می توان با تنظیم k1=k به حالت ساده تر کاهش داد
، k2=∞، c1=∞، c2=c.)
یک معادله مکعبی ممکنه سه ریشه واقعی یا یک ریشه واقعی و دو ریشه مختلط داشته باشه، بسته به تمایز مکعب (اینجا را ببینید)، که به نظر می رسه با تمایز سیستم های کم میرا و بیش از حد برای حالت ساده تر قابل مقایسه باشد. من معتقدم که ارزش این تمایز به این بستگی دارد که آیا سیستم کمتر/بحران/بیش از حد ضعیف است.


