و صلبیت خمشی EI. ایده این است که حرکت جرم را در جهت عمودی با یک سیستم ساده یک درجه آزادی تقریب کنیم، بنابراین اولین قدم در آن محاسبه ضریب سختی معادل سیستم است.
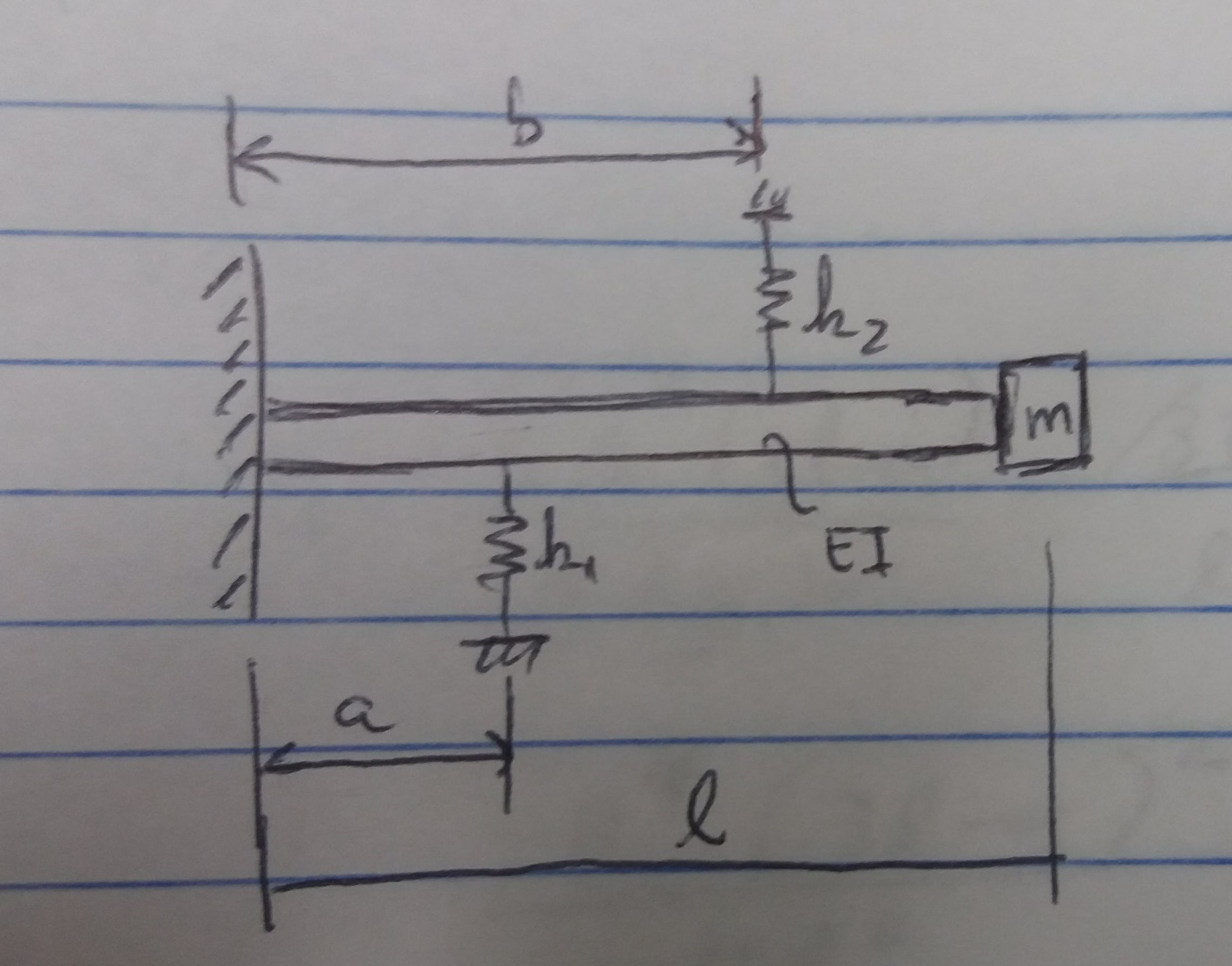
من برای درک راه حل های او مشکل دارم، زیرا کاملاً با صحبت های او موافق نیستم. رویکرد او به مشکل:
با توجه به معادله انحراف یک تیر کنسول با بار P در نوک اعمال می شود،$v=\frac{-Px^2}{6EI}(3l-x)$
او می گوید یک فنر معادل $k_{eq12}$ فنرهای k1 را جایگزین می کند و k2 در سمت راست تیر برای محاسبه $k_{eq12}$
، کل انرژی پتانسیل است$\begin{align}U&=\frac{1}{2}k_{eq_{12}}y_l^2=\frac{1}{2}k_{1}y_a^2+\frac{1}{2}k_{2}y_b^2\\
k_{eq_{12}}&=k_1\left(\frac{y_a}{y_l}\right)^2+k_2\left(\frac{y_b}{y_l}\right)^2
\end{align}$ جایی$y_a$و$y_b$و$y_l$ انحرافات تیر برای بار واقع در a,b ,lهستند
و $y_a$,$y_b$ انحراف فنرها هستند.بنابراین، برای بار واحد،$\begin{align}y_a&=\frac{a^2}{6EI}(3l-a) \tag1\\
y_b&=\frac{b^2}{6EI}(3l-b) \tag2\\
y_l&=\frac{l^3}{3EI} \tag3
\end{align}$
حالا اگر $k_{eq_{12}}$ یک فنر معادل در انتهای سمت راست تیر است، سپس فنر معادل تیر با این فنر معادل سری است، بنابراین فنر معادل کل سیستمی که جرم را تحمل می کند،
$\frac{1}{k_{eq}}=\frac{1}{k_{eq_{12}}}+\frac{1}{k_{beam}}$
جایگزین کردن انحرافات$ya
, yb
, yl$
و سختی معادل تیر $k_{beam}=3EI/l^3$ است، ما گرفتیم
$k_{eq}=\frac{\left( k_1\left(\frac{y_a}{y_l}\right)^2+k_2\left(\frac{y_b}{y_l}\right)^2 \right)k_{beam}}{k_1\left(\frac{y_a}{y_l}\right)^2+k_2\left(\frac{y_b}{y_l}\right)^2+k_{beam}}$
که می توان آن را ساده کرد، جایگزین (1)، (2)، (3) و $k_{beam}$، به
$k_{eq}=\frac{3EIk_1a^4(3l-a)^2+3EIk_2b^4(3l-b)^2}{l^3\left[k_1a^4(3l-a)^2+k_2b^4(3l-b)^2+12l^3EI\right]}$
این پاسخی است که او به ما داد. به ویژه، من با چند مرحله در طول مسیر موافق نیستم، اما نکته کلیدی در اینجا برای من این است که ما نمی توانیم از معادله انحراف برای یک تیر کنسولی یک بار نوک در انتها استفاده کنیم، زیرا این تیر دقیقاً یک تیر کنسول نیست. ، اما دو تکیه گاه اضافی دارد، فنرها.رویکرد من برای این مشکل این خواهد بود که با توجه به بار اعمال شده P
در انتهای سمت چپ، معادله انحراف سیستم با فنرها و سفتی معادل تقریبی را با معادله جدید پیدا کنید. معادله انحراف اکنون باید از $EI\frac{d^4v}{dx^4}=w(x)$ محاسبه شود.
منحنی الاستیک کار بسیار سختتر، زیرا تیری است که توسط دو فنر پشتیبانی میشود و از نظر استاتیکی یک تیر نامشخص است.
استخراج سفتی یک تیر کنسول بارگذاری شده یکنواخت
سختی یک تیر کنسول بارگذاری شده یکنواخت به شرح زیر است:
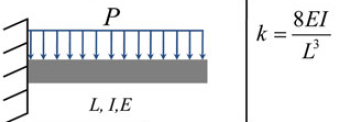
من سعی می کنم سفتی را استخراج کنم، اما با یک مشکل مواجه هستم. خوشحال میشم اگه کسی از بچه های هوپا بتونه کمکم کنه کاری که تا الان انجام دادم:از درک من، سفتی k به عنوان ... تعریف شده$k = \frac{F}{\delta}$
جایی که F نیرویی است که تیر را در نقطه معینی توسط مثلث به حرکت در می آورد
از این رو، من انحراف نوک و بار نقطه ای معادل را در نوک محاسبه می کنم و از این دو مقدار برای بدست آوردن سفتی استفاده می کنم.
من ممیدونم که منحنی انحراف این است:
$y(x) = \frac{p}{24EI}(6L^2x^2-4Lx^3+x^4)$
انحراف نوک تبدیل می شود:
$\delta_{tip} = y(L) = \frac{p}{24EI}(6L^4-4L^4+L^4) = \frac{pL^4}{8EI}$
برای نیروی معادل در نوک، موارد زیر را انجام می دهم:
من بار نقطه ای معادل را محاسبه می کنم
سپس بار نوک معادل را از بار نقطه ای محاسبه می کنم (ممان = 0 در اطراف انتهای ثابت)
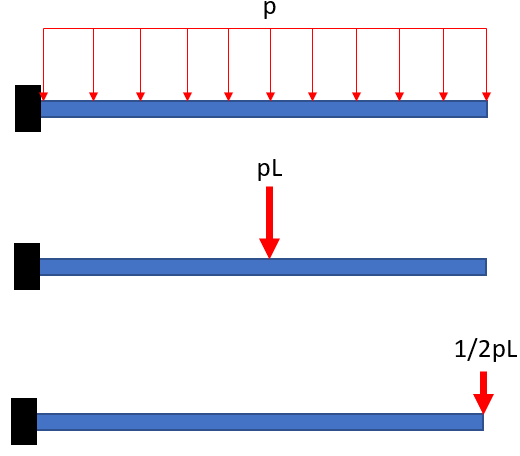
اما پس از آن من با سفتی زیر پایان می دهم:
$k=\frac{\frac{1}{2}pL}{\frac{pL^4}{8EI}} = \frac{4EI}{L^3}$
که اشتباه است...خیلی به جواب نزدیک شدم، درست از کنارش ردشدم
همانطور که گفتم، ضریب سختی به عنوان نیرویی در طول مسافت تعریف میشود: چه مقدار نیروی لازم است برای انحراف یک جسم (مثلاً یک تیر یا یک فنر) به روشی معین در فاصله معینی اعمال کنید.
همانطور که به درستی استخراج کردم انحراف در نقطه یک تیر تحت یک بار توزیع شده است
$\delta = \dfrac{pL^4}{8EI}$
در حال حاضر، این در واقع اساساً پاسخ همان جاست، در واقع. این می گوید که اگر یک بار توزیع شده اعمال کنید p
بر روی یک تیر به یک روش معین، فاصله ای δ را منحرف می کند
. این واقعاً به تعریف ما از ضریب سختی بالا نزدیک است، با این تفاوت که در اینجا ما در مورد بار توزیع شده به جای نیرو صحبت می کنیم.
بنابراین، چگونه می توانیم این بار توزیع شده را به نیرو تبدیل کنیم؟ واقعا خیلی تلاش کردم تنها کاری که باید انجام دهم این است که بار کل P را محاسبه کنم
ایجاد شده توسط بار توزیع شده، که شما به درستی به عنوان مشتق شده است
$P = pL$
. نیازی به انجام هیچ نوع تغییری در محل نیرو یا هر چیز دیگری نیست. اگر فقط آن را به معادله انحراف متصل کنیم، دریافت می کنیم
$\begin{align}
\delta &= \dfrac{PL^3}{8EI} \\
\therefore \dfrac{P}{\delta} &\equiv k = \dfrac{8EI}{L^3}
\end{align}$
نکته ای که در اینجا باید به خاطر داشت این است که ضرایب سختی به بارگذاری دقیق و پیکربندی مرزی داده شده و برای نقطه خاصی که برای آن محاسبه می شوند منحصر به فرد هستند. اگر یک بار توزیع شده را به یک بار متمرکز تبدیل کنید و انحراف حاصل را محاسبه کنید، ضریب سختی متفاوتی دریافت خواهید کرد (در نهایت، یک تیر تحت بارگذاری توزیع شده متفاوت از یک تیر تحت بار متمرکز منحرف می شود). اگر از همان تیر با بارگذاری یکسان استفاده کنید، اما انحراف را در فاصله میانی محاسبه کنید، ضریب سختی دیگری دریافت خواهید کرد. هیچ کدام از این ضرایب اشتباه نیستند، فقط برای موارد مختلف صحیح هستند.
بنابراین محاسبه ضریب سختی مرحله آسانی است: انحراف را در نقطه مورد نظر محاسبه کنید، کل نیروی اعمال شده در کل ساختار را جمع کنید و سپس انحراف را بر آن تقسیم کنید.
دقت کنید شما نیتونید بار توزیع شده را با بار متمرکز به جای انحراف جایگزین کنید. در مورد شما انحراف بارگذاری اصلی اگر $ωL=P$ را بنامیم
است:
$\delta_{max}=\frac{\omega L^4}{8EI}=\frac{P L^3}{8EI}$
اما اگر P را جایگزین کرده و در مرکز تیر قرار دهیم
$\delta_{max}=\frac{5P L^3}{48EI}=5/6 \frac{P L^3}{8EI}$
همانطور که می بینیم جایگزینی منجر به کاهش 1/6 در انعکاس شده است و این باید باشد زیرا قسمت های بار توزیع شده از مرکز تیر در خم کردن آن موثرتر از قسمت های نزدیک به تیر هستند. پشتیبانی با لحظه کمتر


