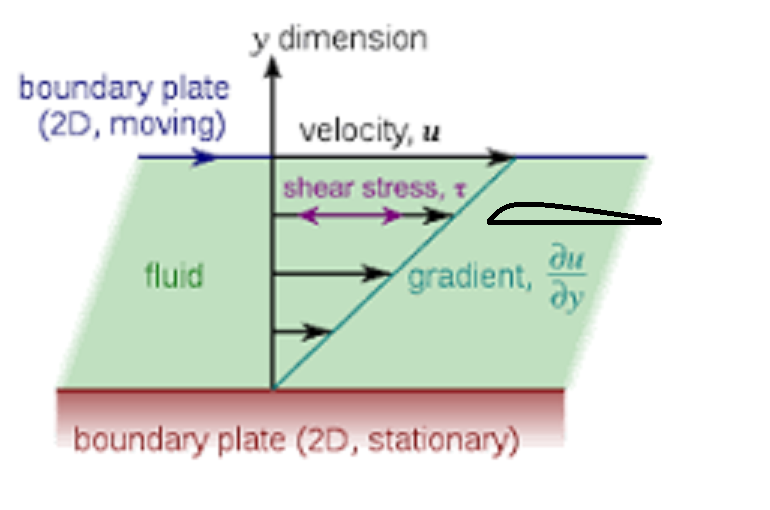
جریان ترکیبی Poiseuille-Couette نکته Pigging به تکنیک تمیز کردن یا بازرسی خط لوله از طریق بازیابی محصولات به دام افتاده در خطوط لوله بدون توقف عملیات اشاره دارد. این کار از طریق قرار دادن دستگاهی به نام pigging pigs در خطوط لوله فرآیند انجام می شود.Pipeline Inspection Gauge
من به طور تصادفی با این تمرین در کتاب "مکانیک سیالات" جیمز فی مواجه شدم، که از آن برای یادگیری دینامیک سیالات به تنهایی استفاده می کنم شکل یک پیگ (وسیلهای است مورد استفاده در لولههای انتقال سیالات از جمله لولههای آب، فاضلاب، انتقال نفت و انتقال گاز. از پیگ معمولاً برای اهداف زیر استفاده میشود:تمیزکاری لوله
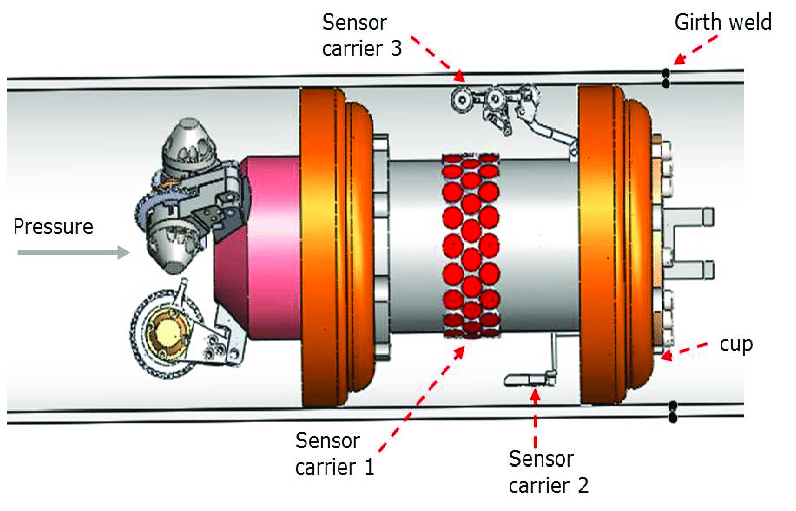
ایجاد حائل فیزیکی بین دو سیال متفاوت
نظارت بر بدنه لوله
ضبط اطلاعات هندسی خط لوله
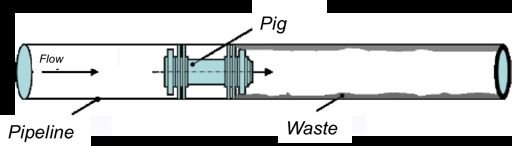
به کار استفاده از پیگ در داخل لولهها، «پیگرانی» گفته میشود. پیگرانی بدون متوقف کردن جریان سیال امکانپذیر است.
پیگهای اولیه تنها برای تمیز کردن لوله – به عنوان روشی کمهزینه و سریع – مورد استفاده قرار میگرفتهاند؛ و در حال حاضر نیز پیگرانی معمولی (تنها برای تمیزکاری) استفادهٔ فراوانی دارد. پیگرانی هوشمند، توسط پیگهای هوشمند انجام میشود که وظایفی از قبیل نظارت بر بدنهٔ لوله و ضبط اطلاعات هندسی لوله را نیز به عهده دارند. )ّبه طول L را در داخل لوله ای به شعاع a نشان می دهد که دارای فاصله شعاعی h<<a بین سطح آن و سطح داخلی لوله است. هنگامی که فشار P1 در 1 از فشار P2 در 2 بیشتر شود، پیگ با سرعت ثابت V به سمت راست حرکت می کند. با فرض اینکه جریان بین پیگ و دیواره لوله را می توان به عنوان یک صفحه ثابت کوئت به اضافه جریان پوازی در نظر گرفت. در یک چارچوب مرجع متصل به pig.
(الف) یک عبارت برای سرعت پیگ V بر حسب پارامترهای P1، P2، L، h، a و ویسکوزیته سیال ν استخراج کنید. (ب) اگر Q نرخ جریان حجمی سیال است که از شکاف خلاصی نشت می کند، نسبت به پیگ، عبارتی برای نسبت $Q/\pi a^2V$ بدست آورید که نسبت نرخ نشت به سرعت جریان سیال از طریق لوله است.
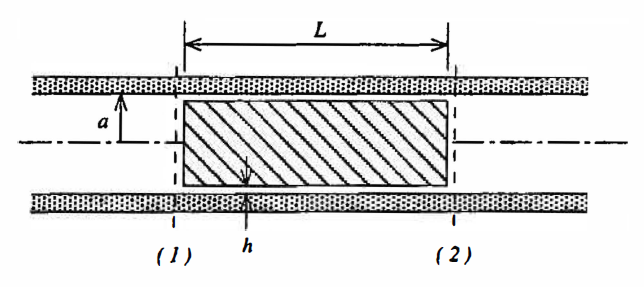
من سعی کردم الف) را حل کنم و نکته استفاده از جریان نوع کوئت به اضافه پوازوی را دنبال کنم. اگر یک قاب مرجع را به پیگ (محور x آن که در سطح pig قرار دارد و با محور استوانه موازی است و محور y عمود بر آن) وصل کنم، می بینیم که شرط عدم لغزش به این معنی است که$u(y=0)=0$. علاوه بر این، می بینیم که در $y=h$،$ u(h)=V$، که در آن V بزرگی سرعت پیگ در چارچوب آزمایشگاهی است. می توان ثابت کرد که سرعت سیال در شکاف دیواره pig برابر است با:
$u(y)=V\frac{y}{h}+\frac{1}{2\mu}(-\frac{dp}{dx})y(h-y)$
حال، اگر به درستی متوجه شده باشم، مشکل از من می خواهد که V را به عنوان تابعی از پارامترهای فوق به دست بیاورم. با این حال، من در این مرحله گیر کرده ام، زیرا پس از جداسازی V، هیچ ایده ای در مورد اینکه چگونه از وابستگی u آن خلاص شوم، ندارم. من می توانم عبارت $\frac{dP}{dx}$ را با توجه به اینکه این فقط $$\frac{P_2-P_1}{L} است حذف کنم، اما تمام.
ادغام در y برای بدست آوردن نسبت $\frac{Q}{W}$ بازده:
$\frac{Q}{W}=\frac{Vh}{2}+\frac{h^3}{12\mu}(\frac{P_2-P_1}{L})$
بنابراین $V=\frac{2Q}{hW}-\frac{h^2}{6\mu}(\frac{P_2-P_1}{L})=\frac{Q}{h\pi a}-\frac{h^2}{6\mu}(\frac{P_2-P_1}{L})$
سیال دینامیک مرزی شرایط جریان ناویر استوکس
همانطور که از چارچوب مرجع پلاگین محاسبه می شود، معادلات شما باید به شرح زیر باشد:
$u(y)=-V\frac{y}{h}+\frac{1}{2\mu}(-\frac{dp}{dx})y(h-y)\tag{1}$
$\frac{Q}{W}=-\frac{Vh}{2}-\frac{h^3}{12\mu}(\frac{P_2-P_1}{L})\tag{2}$
جایی که y = 0 در سطح دوشاخه است. اگر Eqn را متمایز کنیم. 1 با توجه به y و ارزیابی گرادیان سرعت در y = 0، به دست می آوریم:
$\frac{du}{dy}(0)=-\frac{V}{h}-\frac{h}{2\mu}\frac{P_2-P_1}{L}$
بنابراین تنش برشی روی دوشاخه است
$\tau=-\mu\frac{V}{h}-\frac{h}{2}\frac{(P_2-P_1)}{L}$
بنابراین، موازنه نیرو روی دوشاخه باید به صورت زیر باشد:
$\pi a^2(P_1-P_2)-2\pi aL\left(\mu\frac{V}{h}+\frac{h}{2}\frac{(P_2-P_1)}{L}\right)=0$
این منجر به:
$(P_1-P_2)\left(1+\frac{h}{a}\right)=\frac{2L}{a}\mu\frac{V}{h}$
از آنجایی که h<<R، این به:
$\frac{(P_1-P_2)}{L}=\frac{2}{a}\mu \frac{V}{h}$
حل سرعت محوری در کانال در مختصات استوانهای با شرایط مرزی u(a)=0 و u(a−h)=V به دست میآید:
$u\left(r\right)=-\frac{1}{4}\frac{\Delta p}{\mu L}r^{2}+\frac{K_{1}}{\mu}\ln r+K_{2}$
جایی که:
$K_{1}=\frac{\mu V-\frac{\Delta p a^{2}}{L}\left(\frac{1}{2}\frac{h}{a}\right)\left(1-\frac{1}{2}\frac{h}{a}\right)}{\ln\left(1-\frac{h}{a}\right)} \qquad K_2=\frac{1}{4}\frac{\Delta p}{\mu L}a^{2}-\frac{K_{1}}{\mu}\ln a$
تنش برشی در سطح داخلی لوله عبارت است از:
$\tau(a)=-\mu\frac{d u}{d r}(a)=\frac{1}{2}\frac{\Delta p}{L}a+\frac{K_{1}}{a}$
پس از تجزیه و تحلیل چستر، در حالت ثابت، افت فشار در سراسر پیگ باید برابر با نیروی اصطکاک در دیوار باشد، به عنوان مثال:
$\pi a^{2}\Delta p=2\pi aL\tau\left(a\right)$
با جایگزینی عبارت برای تنش برشی در دیوار و تنظیم مجدد برای V، متوجه میشویم:
$V=\frac{\Delta pa^{2}}{\mu L}\left(\frac{1}{2}\frac{h}{a}\right)\left(1-\frac{1}{2}\frac{h}{a}\right)$
واضح است که اگر تقریب کانال کوچک $\frac{h}{a}\ll 1$ را اعمال کنیم، در نهایت معادله چستر را خواهیم داشت. همچنین توجه داشته باشید که ثابت ها به صورت زیر ساده می شوند:
$K_{1}=0 \qquad K_2=\frac{1}{4}\frac{\Delta p}{\mu L}a^{2}$
این نشان می دهد که ما می توانیم به طور کامل از هر گونه اثرات ناشی از انحنا در کانال چشم پوشی کنیم.
اکنون می توانیم ادامه دهیم و جریان نشت کسری را حل کنیم. ابتدا ثابت ها را جایگزین می کنیم و ساده می کنیم:
$u\left(r\right)=-\frac{1}{4}\frac{\Delta p}{\mu L}\left(r^{2}-a^{2}\right)$
نرخ جریان از طریق شکاف:
$Q = \int_A u dA = 2\pi\int_{a-h}^a rudr = 2\pi\frac{\Delta p a^{4}}{\mu L}\left(\frac{1}{2}\frac{h}{a}\right)^{2}\left(1-\frac{1}{2}\frac{h}{a}\right)^{2}$
در این صورت نشت کسری به صورت زیر است:
$\frac{Q}{\pi a^2 V} = \frac{h}{a}\left(1-\frac{1}{2}\frac{h}{a}\right) \approx \frac{h}{a}$
که کاملاً با ارتفاع نسبی کانال بین پیگ و سطح داخلی لوله تعیین می شود (شاید جای تعجب نباشد)...I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering



رهام حسامی ترم هفتم مهندسی هوافضا