برای سوال من این است که اغلب از استادها میشنوم که دینامیک لاگرانژی عمومی تر و قدرتمندتر از رویکرد نیوتن است. درسته. اما، من می خواهم برای خودم ببینم که درست است. در مورد این مشکل خاص، که دشوارتر از مسائل پایه نیوتنی است، راه حل دشوار ه اما هنوز ممکنه .
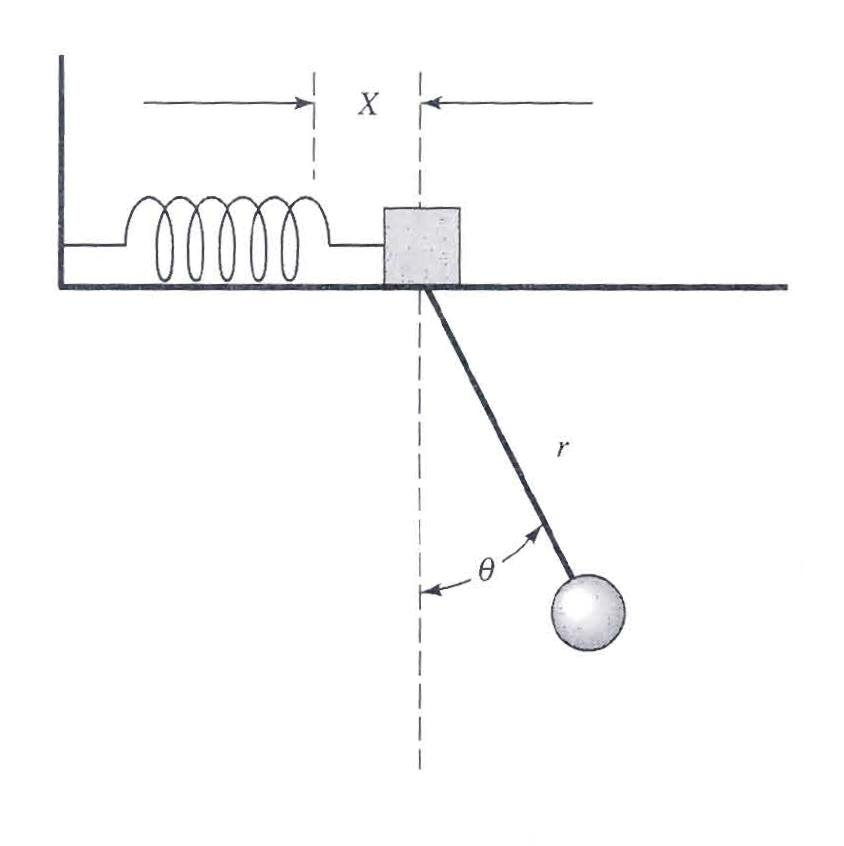
مفاهیم نوسانگر اجباری، میرایی، ساده و جفت شده برای من و معادلات دیفرانسیل معمولی پایه کاملاً واضح است.شما اولین مرحله را انجام دادید و آن تشخیص درجه آزادی سیستم (x و θ) است. اجازه دهید بدنه بلوک [1] و بدنه کروی [2] و طول میله را$ ℓ$ بنامیم.
سینماتیک
موقعیت مفاصل و مراکز جرم را تابعی از درجات آزادی بیان کنید. مثلا
${\bf r}_{2} = ( x + \ell \sin \theta, -\ell \cos \theta,0)$
سرعت های چرخشی را به روشی مشابه بیان کنید
${\boldsymbol \omega}_2 = \dot{\theta} {\bf \hat{z}}$
مشتق کل موقعیت را برای یافتن سرعت و سپس شتاب مراکز جرم بگیرید. مثلا
${\bf v}_2 = (\dot{x} + \dot{\theta} \ell \cos\theta, \dot{\theta} \ell \sin \theta,0)$
و${\bf a}_2 = (\ddot{x} + \ddot{\theta} \ell \cos\theta - \ell \dot{\theta}^2 \sin \theta, \ddot{\theta} \ell \sin \theta + \ell \dot{\theta}^2 \cos \theta,0)$
مشتق کل سرعت دورانی را برای شتاب دورانی در نظر بگیرید
${\boldsymbol \alpha}_2 = \ddot{\theta}{\bf \hat{z}}$
پویایی شناسی
یک نمودار بدن آزاد برای هر جسم انجام دهید و نیروهای وارد بر هر جسم و گشتاورهای مربوط به مرکز جرم هر جسم را جمع آوری کنید. برای هر مفصل نیروهای واکنشی مناسب را روی جسم بعدی و نیروهای مساوی و مخالف را روی جسم قبلی اعمال کنید. به عنوان مثال (با در نظر گرفتن کشش T، اصطکاک f1 و نیروی نرمال n1)
$\begin{align}
\Sigma {\bf F}_1 & = {\bf T}_{12} + {\bf W}_1 & \Sigma {\bf F}_2 & = -{\bf T}_{12} + {\bf W}_2 \\
& = \begin{pmatrix} T \sin\theta+f_1 \\ -T \cos\theta-m_1 g+n_1 \\ 0 \end{pmatrix} & & = \begin{pmatrix} -T \sin\theta \\ T \cos\theta-m_2 g \\ 0 \end{pmatrix}
\end{align}$W نیروهای اعمال شده و نیروهای مشترک داخلی T را مشخص می کند
معادلات حرکت
$\begin{align}
\Sigma {\bf F}_1 & = m_1 {\bf a}_1 &\Sigma {\bf F}_2 & = m_2 {\bf a}_2 \\
\Sigma {\bf M}_1 & = I_1 {\boldsymbol \alpha}_1 + {\boldsymbol \omega}_1 \times I_1 {\boldsymbol \omega}_1 & \Sigma {\bf M}_2 & = I_2 {\boldsymbol \alpha}_2 + {\boldsymbol \omega}_2 \times I_2 {\boldsymbol \omega}_2
\end{align}$
باید مراقب مسائل سه بعدی بود تا گشتاور جرمی ماتریس اینرسی را در امتداد مختصات کلی بیان کنیم و نه مختصاتجسم. $I = {\rm R} I_{body} {\rm R}^\top$helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



