در اینجا من دو استدلال دارم:
این میله در اثر گرانش دارای گشتاور نامتعادل حول محور چرخش است. واکنش عادی از محور چرخش می گذرد و از این رو هیچ گشتاوری در اطراف محور ثابت ندارد. بنابراین میله باید با گذشت زمان به محور نزدیکتر شود.
ممکن است اتفاق بیفتد که مولفه افقی نرمال شتاب مرکزگرا و مولفه عمودی نرمال گرانش را متعادل می کند. از این رو مرکز جرم ممکن است در یک صفحه ثابت دستخوش حرکت دایره ای شود.
Cleary 1 و 2 با هم تضاد دارند. اما من همچنین احساس می کنم که 1 و 2 باید ثابت باشند و من یک چیز بزرگ را اینجا از دست داده ام.
من اینجا چه چیزی را افراموش کردم چگونه میله می تواند در حالت تعادل بماند؟
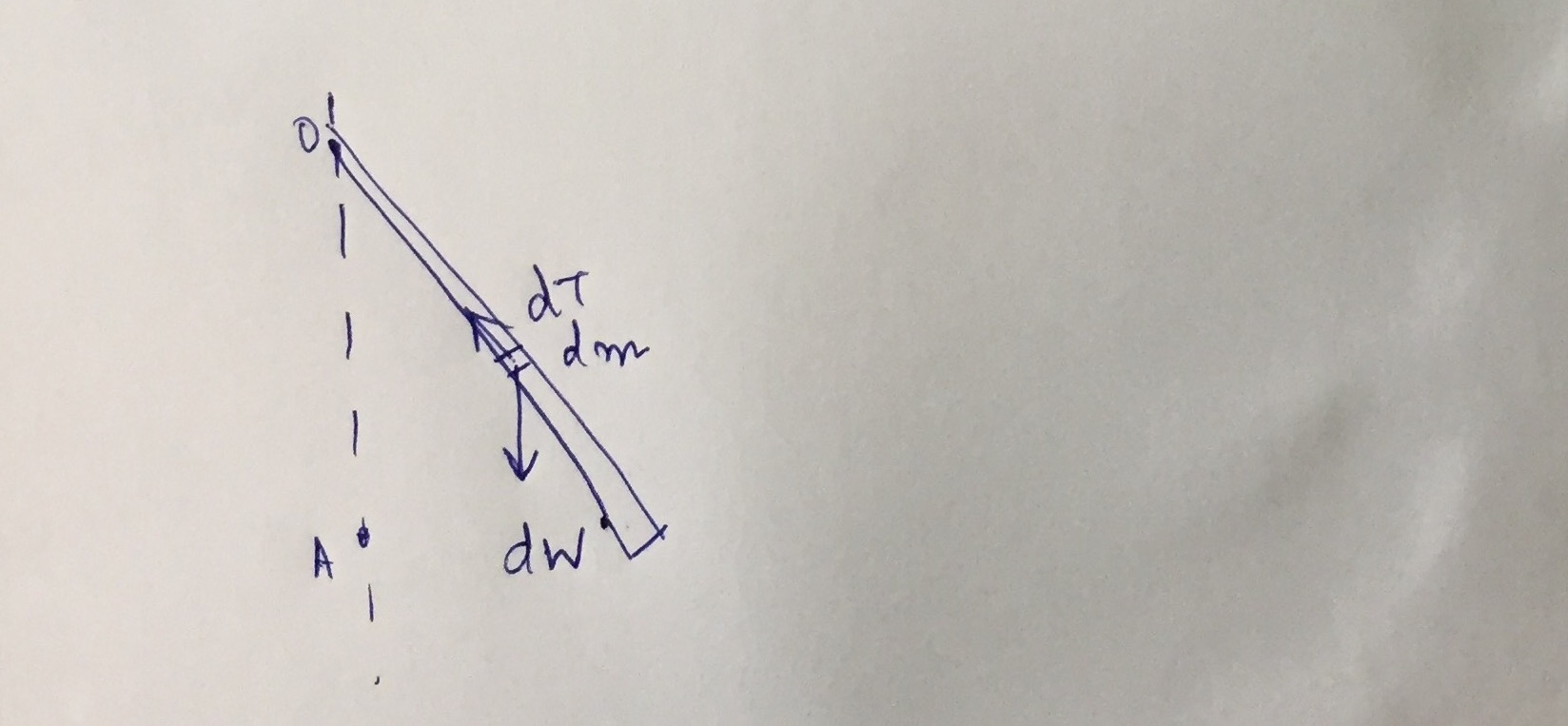
من راهی برای توضیح تعادل در میله با گرفتن جرم های اولیه و در نظر گرفتن هر قسمت به عنوان یک آونگ مخروطی ایجاد کرده ام.
با این حال، وقتی میله را به طور کامل می‌گیرم:
در اینجا تکانه زاویه ای میله حول محور Y ثابت است حتی اگر یک گشتاور خالص عمل کند.
در اینجا تکانه زاویه ای میله حول محور Y ثابت است حتی اگر یک گشتاور خالص در حال عمل باشد. این درست نیست.
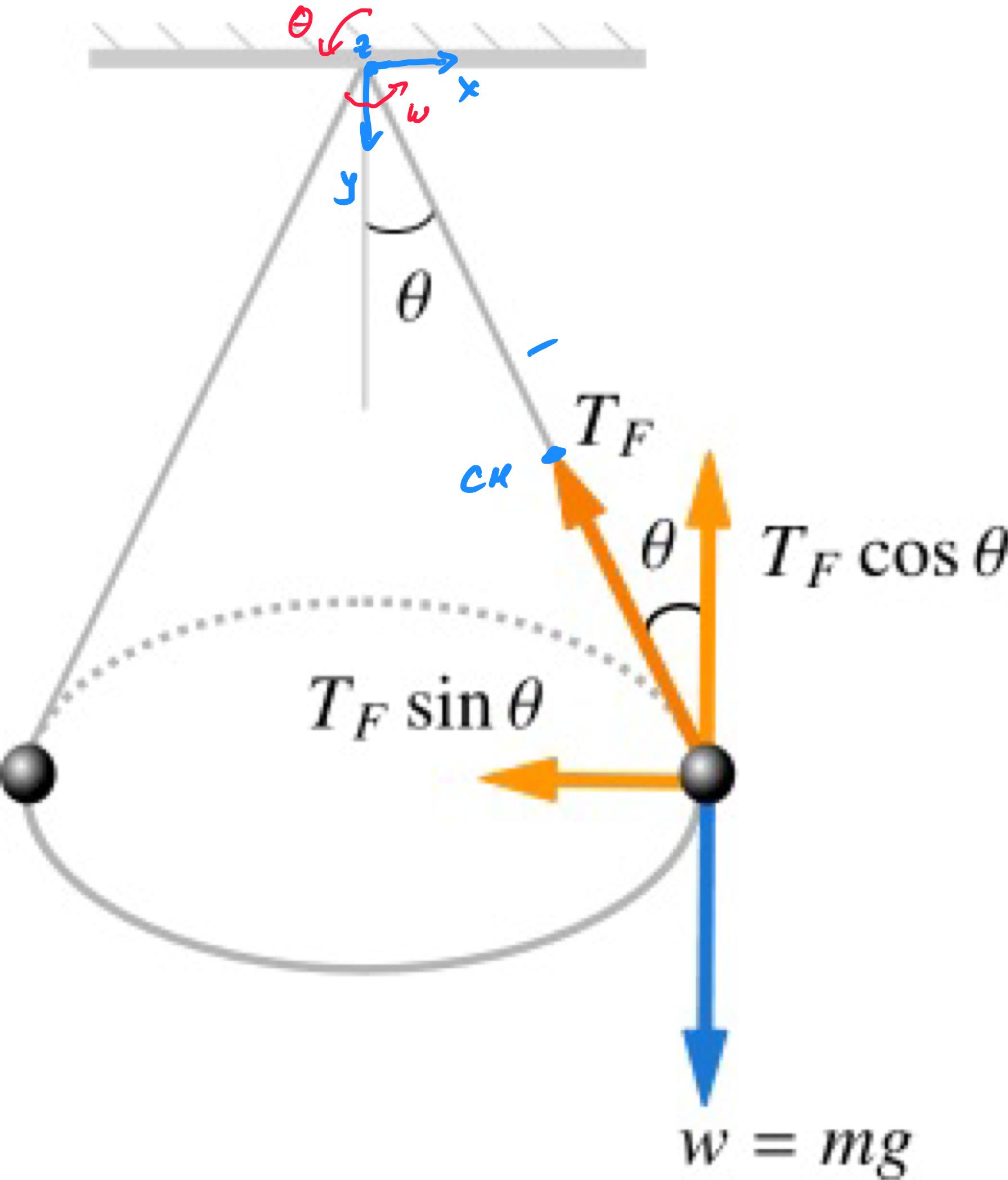
توجه داشته باشید که تکانه زاویه ای ثابت نیست. بستگی به مبدا دارد. گرفتن مبدا در نقطه حمایت، در بالای میله. همانطور که در شکل نشان داده شده است، تکانه زاویه ای حاصل عمود بر میله است.
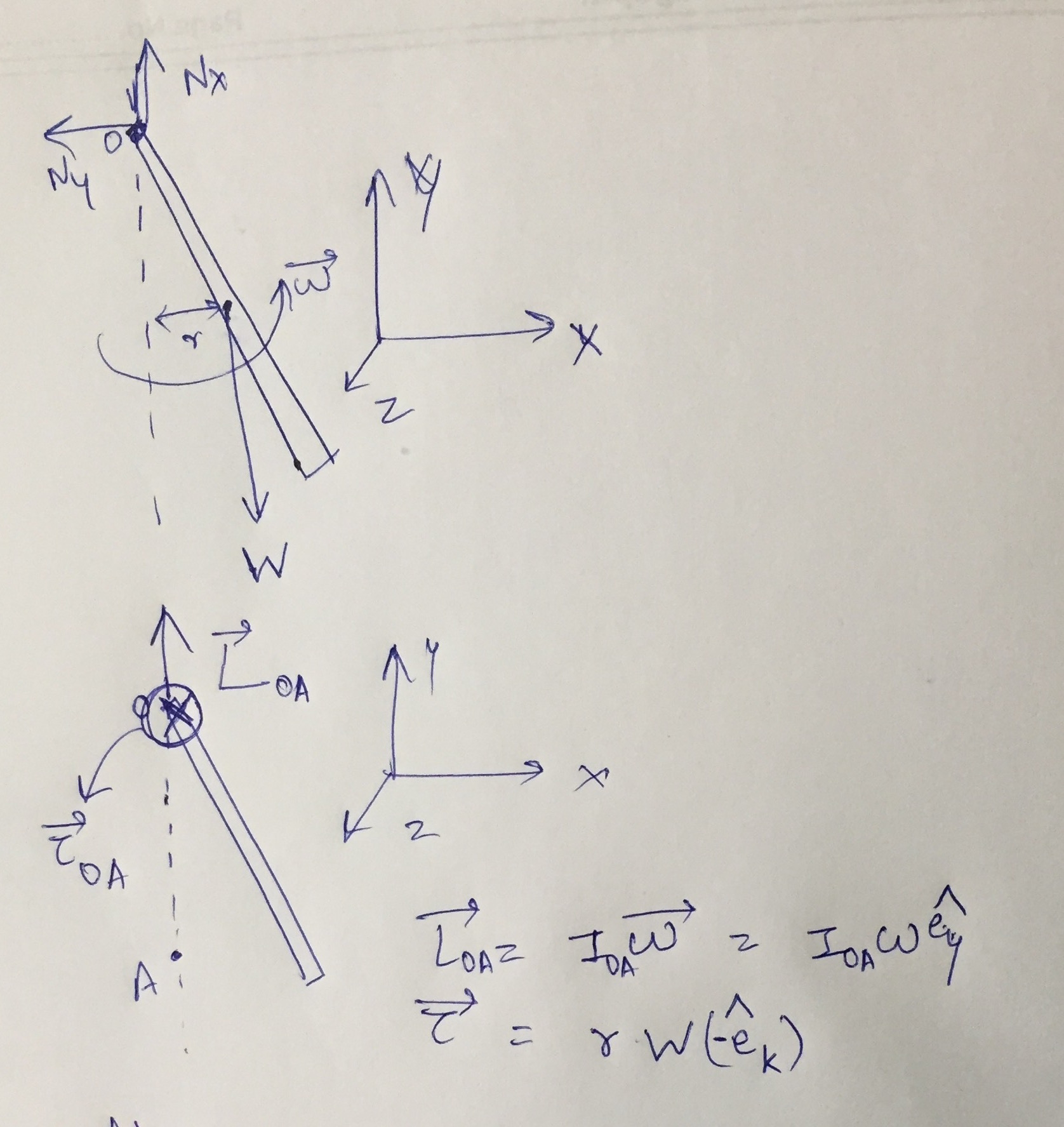
$\vec{L} = \int \vec{r} \times \vec{v} \rho dr,$
که ρ چگالی خطی میله است.
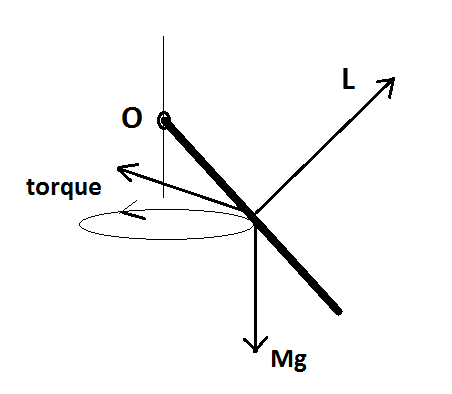
بنابراین، تکانه زاویه ای در بالای یک مخروط در حال چرخش است در شکل من. گشتاور در مرکز جرم $\vec{\tau} = \vec{r} \times \vec{f}_g$ به بردار در صفحه افقی تبدیل می شود. همانطور که تکانه زاویه ای در اطراف مخروط پیش می رود، گشتاور نیروی محرکه ای برای چرخش $\vec{L}$ است.
$\frac{\Delta \vec{L}}{\Delta t} = \vec{\tau}.$
با تفکر در معادله$\vec{L} = I \vec{\omega}$، یادآوری می شود که گشتاور اینرسی I یک ماتریس متقارن 3×3 است و در این حالت، عناصر ماتریس تابعی از زمان هستند. این I(t) وابسته به زمان منجر به یک تکانه زاویه ای پردازش می شود، $\vec{L}(t)$، حتی اگر $\vec{\omega}$ یک بردار ثابت باشد.$\vec{L} (t)=
\begin{bmatrix}
I_{xx}(t) & I_{xy}(t) & I_{xz}(t) \\
I_{xy}(t) & I_{yy}(t) & I_{yz}(t) \\
I_{xz}(t) & I_{yz}(t) & I_{zz}(t)
\end{bmatrix}
\times
\begin{bmatrix}
0\\
0 \\
\omega
\end{bmatrix}$
عناصر ماتریس گشتاور اینرسی تابعی از زمان هستند زیرا ما یک قاب مختصات ثابت را تنظیم می کنیم و عناصر ماتریس را محاسبه می کنیم، به عنوان مثال. $I_{xy} = -\int x y \rho d l$ زمانی که نه حول مرکز ثقل و نه بر روی یک محور اصلی می چرخد، یک وضعیت کلی است.
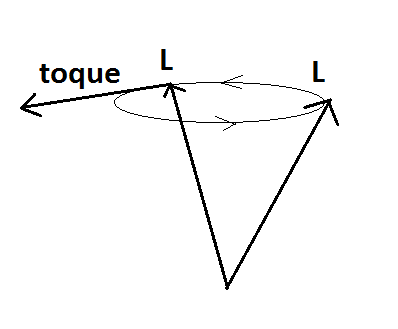. تقدم حرکت زاویه ای.برای رسیدن به این پیکربندی حالت پایدار، می توانید از معادله حرکت در مرکز جرم به دست آورید که بزرگی سرعت زاویه ای ω باید باشد:$\omega^2=2\,{\frac {mgL}{\cos \left( \theta \right) \left( {L}^{2}m+4\,{\it I_x
}-4\,{\it I_y} \right) }}$
θ زاویه ثابت بین میله و محور عمودی L طول میله و $~I_x~,I_y~$ اینرسی های میله در مورد محور x و y محلی هستند. با$~I_x=I_y$⇒
$\omega^2=\frac{2\,g}{L\cos(\theta)}$
معادلات
انتقال
بردار را در CM قرار دهید.$\begin{align*}
&\text{Position vector to the CM }\\
&\vec{R}=S_y(\omega\,\tau)\,\frac{L}{2}\left[ \begin {array}{c} \sin \left( \theta \right)
\\ \cos \left( \theta \right)
\\ 0\end {array} \right]\\
&\text{with}\\
&S_y= \left[ \begin {array}{ccc} \cos \left( \omega\,\tau \right) &0&\sin
\left( \omega\,\tau \right) \\ 0&1&0
\\ -\sin \left( \omega\,\tau \right) &0&\cos \left(
\omega\,\tau \right) \end {array} \right]\\
&\Rightarrow\\
&\text{kinetic energy}\\
&T_T=\frac{m}{2}\vec{\dot{R}}^T\,\vec{\dot{R}}\\
&\text{potential energy}\\
&U=-m\,g\,\vec{R}_y
\end{align*}$
چرخش
ماتریس تبدیل $\begin{align*}
&\text{transformation matrix}\\
&S=S_y(\omega\,\tau)\,S_z(\theta)\\
&S_z=\left[ \begin {array}{ccc} \cos \left( \theta \right) &-\sin \left(
\theta \right) &0\\ \sin \left( \theta \right) &\cos
\left( \theta \right) &0\\ 0&0&1\end {array}
\right]\\
&\Rightarrow\\
&\vec{\Omega}= \left[ \begin {array}{c} \sin \left( \omega\,\tau \right) \dot\theta
\\ \omega\\ \cos \left( \omega\,
\tau \right) \dot\theta \end {array} \right]\\
&\text{kinetic energy}\\
&T_R=\frac{1}{2}\vec{\Omega}^T\,S^T\,\Theta\,S\,\vec{\Omega}\\\\
&\text{where $~\Theta~$ the rod inertia tensor }\\
&\Theta=\left[ \begin {array}{ccc} J_{{x}}&0&0\\ 0&J_{{y}}&0
\\ 0&0&J_{{z}}\end {array} \right]\\
&\text{the lagrangian }\\
&\mathcal{L}=\frac 18\,{\dot\theta }^{2} \left( {L}^{2}m+4\,J_{{z}} \right) +\frac 12\,mgL\cos
\left( \theta \right)\\& -\frac 18\,{\omega}^{2} \left( -{L}^{2}m+{L}^{2}m
\left( \cos \left( \theta \right) \right) ^{2}-4\,J_{{x}}+4\,J_{{x}}
\left( \cos \left( \theta \right) \right) ^{2}-4\, \left( \cos
\left( \theta \right) \right) ^{2}J_{{y}} \right)
\end{align*}$
از اینجا می توانید معادله حرکت را بدست آورید
$\begin{align*}
&\text{transformation matrix}\\
&S=S_y(\omega\,\tau)\,S_z(\theta)\\
&S_z=\left[ \begin {array}{ccc} \cos \left( \theta \right) &-\sin \left(
\theta \right) &0\\ \sin \left( \theta \right) &\cos
\left( \theta \right) &0\\ 0&0&1\end {array}
\right]\\
&\Rightarrow\\
&\vec{\Omega}= \left[ \begin {array}{c} \sin \left( \omega\,\tau \right) \dot\theta
\\ \omega\\ \cos \left( \omega\,
\tau \right) \dot\theta \end {array} \right]\\
&\text{kinetic energy}\\
&T_R=\frac{1}{2}\vec{\Omega}^T\,S^T\,\Theta\,S\,\vec{\Omega}\\\\
&\text{where $~\Theta~$ the rod inertia tensor }\\
&\Theta=\left[ \begin {array}{ccc} J_{{x}}&0&0\\ 0&J_{{y}}&0
\\ 0&0&J_{{z}}\end {array} \right]\\
&\text{the lagrangian }\\
&\mathcal{L}=\frac 18\,{\dot\theta }^{2} \left( {L}^{2}m+4\,J_{{z}} \right) +\frac 12\,mgL\cos
\left( \theta \right)\\& -\frac 18\,{\omega}^{2} \left( -{L}^{2}m+{L}^{2}m
\left( \cos \left( \theta \right) \right) ^{2}-4\,J_{{x}}+4\,J_{{x}}
\left( \cos \left( \theta \right) \right) ^{2}-4\, \left( \cos
\left( \theta \right) \right) ^{2}J_{{y}} \right)
\end{align*}$
از اینجا می توانید معادله حرکت را بدست آورید
$\begin{align*}
& \left( \frac 14\,{L}^{2}m+J_{{z}} \right) \ddot\theta \\&+ \left( -\frac 14\,m{
L}^{2}\cos \left( \theta \right) -J_{{x}}\cos \left( \theta \right) +
\cos \left( \theta \right) J_{{y}} \right) \sin \left( \theta \right)
{\omega}^{2}\\&+\frac 12\,mgL\sin \left( \theta \right)=0\tag 1
\end{align*}$
حالت ثابت به این معنی است که$~\ddot{\theta}=0~$معادله را حل می کند. (1) برای $~\omega^2$و راه حل فوق را بدست می آوریدhope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering
رهام حسامی ترم ششم مهندسی هوافضا
ا
