اثر مگنوس یک پدیده قابل مشاهده است که معمولاً با یک جسم در حال چرخش در حال حرکت در یک سیال همراه است. مسیر جسم در حال چرخش به گونه‌ای منحرف می‌شود که وقتی جسم در حال چرخش نیست وجود ندارد. انحراف را می توان با تفاوت فشار سیال در طرف مقابل جسم در حال چرخش توضیح داد. اثر مگنوس به سرعت چرخش بستگی دارد.نیروی گرادیان فشار، نیرویی است که زمانی ایجاد می‌شود که در یک سطح اختلاف فشار وجود داشته باشد. به طور کلی، فشار نیرویی در واحد سطح، در سراسر یک سطح است. اختلاف فشار در یک سطح به معنای تفاوت نیرو است که می تواند منجر به شتابی مطابق قانون دوم حرکت نیوتن شود، اگر نیروی اضافی برای متعادل کردن آن وجود نداشته باشد. نیروی حاصله همیشه از ناحیه پرفشار به ناحیه کم فشار هدایت می شود. هنگامی که یک سیال در حالت تعادل است (یعنی هیچ نیروی خالصی وجود ندارد و هیچ شتابی وجود ندارد)، سیستم در حالت تعادل هیدرواستاتیکی نامیده می شود. در مورد اتمسفر، نیروی گرادیان فشار توسط نیروی گرانشی متعادل می شود و تعادل هیدرواستاتیکی را حفظ می کند. به عنوان مثال، در جو زمین، فشار هوا در ارتفاعات بالای سطح زمین کاهش می‌یابد، بنابراین یک نیروی گرادیان فشار ایجاد می‌کند که با نیروی گرانش روی جو مقابله می‌کند.نیروی مغناطیسی یک جسم در حال چرخش اختلاف فشار بین دو طرف مقابل جسم است که با سطح مقطع مقیاس بندی می شود:
${\displaystyle F_{A}=\Delta p\cdot A=c_{A}\cdot {\frac {\varrho }{2}}(u_{1}^{2}-u_{2}^{2} )\cdot A}$
که در آن ${\displaystyle c_{a}}$ یک عدد اسکالر وابسته به شکل و ماده جسم در حال چرخش است، ${\displaystyle u}$ سرعت سیال نسبت به هر سطح و ${\displaystyle \varrho }$ چگالی سیال است.
هنگامی که برای سرعت چرخش یک توپ صاف حل شود، نیروی حاصل به صورت داده می شود
${\displaystyle {\vec {F}}={\frac {4}{3}}\pi \varrho r^{3}\cdot ({\vec {w}}\times {\vec {v}}) }$
براساس قانون اول نیوتن، تا زمانی که نیرویی به جسم وارد نشود، سرعت و مسیر حرکت آن جسم، تغییر نخواهد کرد فرض کرده وقتی بازیکنی به توپ ضربه می‌زند، سرعت و مسیر حرکت اولیه توپ مشخص می‌شود. پس در میانه راه، چه نیرویی جهت توپ را تغییر می‌دهد؟ پاسخ این سؤال در حرکت اسپین توپ نهفته است. هنگامی که زننده ضربه، نقطه‌ای غیر از مرکز توپ را هدف می‌گیرد، توپ شروع به چرخیدن به دور محور خودش می‌کند. در این حالت، توپ از روی زمین بلند شده و به حرکت درمی‌آید. هوا در دو طرف (چپ و راست) توپ جریان دارد و رفته رفته از سرعت آن می‌کاهد. در یک سمت، حرکت هوا در خلاف جهت چرخش توپ است. در نتیجه، فشار افزایش می‌یابد. در طرف دیگر، هوا و چرخش توپ هم جهت هستند. در این ناحیه، افت فشار اتفاق می‌افتد استوانه‌ای چرخان را در مسیر جریان نشان می‌دهد. در چنین شرایطی، تابع جریان را می‌توان به صورت زیر نوشت کهبا محاسبه مشتق تابع جریان به طریق زیر، سرعت‌های شعاعی و مماسی به دست خواهند آمد.$\large V_r = \frac {1}{r} \frac{\partial \psi}{\partial \theta} = V_\infty \cos\theta (1- \frac {R^2}{r^2})\\~\\
\large V_\theta = \: – \frac{\partial \psi}{\partial r} = \: – V_\infty \sin\theta (1+ \frac {R^2}{r^2}) \: – \frac {\Gamma}{2\pi r}
{roham}$,$\large V_r = \frac {1}{r} \frac{\partial \psi}{\partial \theta} = V_\infty \cos\theta (1- \frac {R^2}{r^2})\\~\\
\large V_\theta = \: – \frac{\partial \psi}{\partial r} = \: – V_\infty \sin\theta (1+ \frac {R^2}{r^2}) \: – \frac {\Gamma}{2\pi r}
{roham }$ سرعت و فشار را روی سطح به دست می‌آوریم. روی سطح استوانه، r=Rو $\large V_r = 0\\~\\
\large V_\theta = \: -2V_\infty\sin\theta \: – \frac {\Gamma}{2\pi r}\\~\\
\large C_p(\theta) = 1-\frac {V^2}{V^2_\infty} = 1-4\sin^2\theta \: – (\frac {\Gamma}{2\pi V_\infty R})^2-(\frac {2\Gamma}{\pi V_\infty R})\sin \theta
{"roham}$ضریب فشار سطحی را نشان می‌دهد. برای به دست آوردن نیروی برآیند، باید از نیروی فشار روی سطح استوانه انتگرال بگیرم
.$\large \overrightarrow{R} \equiv \overrightarrow{D} \hat{i} + \overrightarrow{L} \hat{j} = \huge { \oint_{} \large {-p \hat{n}dA}}
$رابطه بالا را با توجه به شکل پایین، برحسب دو مؤلفه در جهت محورهای x و y بنویسیم. با تقسیم این مؤلفه‌ها به عبارت $\large \frac {1}{2}\rho V^2_\infty \times 2R
$ ضرایب درگ و لیفت به صورت زیر، قابل محاسبه است.$\large c_d = \frac {1}{2R} \oint -C_p n_x dA\\~\\
\large c_l = \frac {1}{2R} \oint -C_p n_y dA
{"roham}$,$\large n_x = \cos \theta, ~~~~ n_y = \sin \theta, ~~~~ dA = R d \theta
$اکنون با کمک رابطه‌های بالا و جای‌گذاری مقدار ضریب فشار سطحی، ضرایب درگ و لیفت به شکل زیر بازنویسی می‌شود.$\large c_d = \frac {1} {2} \int_{0}^{2\pi} -C_p \cos \theta d\theta = \frac {1} {2} \int_{0}^{2\pi} [-1 + 4 \sin^2 \theta + (\frac {\Gamma} {2 \pi V_ \infty R})^2 + (\frac {2 \Gamma} { \pi V_ \infty R}) \sin \theta] \cos \theta d \theta \\~\\
\large c_l = \frac {1} {2} \int_{0}^{2\pi} -C_p \sin \theta d\theta = \frac {1} {2} \int_{0}^{2\pi} [-1 + 4 \sin^2 \theta + (\frac {\Gamma} {2 \pi V_ \infty R})^2 + (\frac {2 \Gamma} { \pi V_ \infty R}) \sin \theta] \sin \theta d \theta
{"roham}$با محاسبه دو انتگرال، مقدار این دو ضریب به دست می‌آید$\large c_d = 0 , ~~~~~ c_l = \frac {\Gamma}{V_\infty R}
$صفر شدن ضریب درگ در رابطه بالا، به عنوان پارادوکس دالامبر شناخته می‌شود. زیرا طبق مشاهدات، می‌دانیم به تمامی اجسام در جریان یکنواخت، همواره نیروی درگ وارد می‌شود. البته این اتفاق، غیر از چشم‌پوشی از ویسکوزیته، دلیل دیگری ندارد. با استفاده از ضریب لیفت، نیروی لیفت به صورت $\large \rho V_\infty \Gamma
$ تعریف می‌شود. این نتیجه، به عنوان نظریه «کوتا – جوکوفسکی» (Kutta-Joukowsky) شناخته می‌شود و برای تمام اجسام دو بعدی معتبر است.در جریان واقعیِ ویسکوز روی یک استوانه با عدد رینولدز بالا، جدایش جریان و نیروی درگ، بزرگ خواهد بود. در حالت عادی، جریان در بین بالا و پایین استوانه صفر است و نیروی لیفتی وارد نخواهد شد. اما اگر استوانه، سرعت زاویه‌ای هم داشته باشد، جدایش جریان موجب به هم زدن تقارن جریان می‌شود. در اینجا اثر مگنوس رخ می‌دهد. ممکن است نیروی لیفت در این حالت، از نیروی لیفت بال هواپیما با همین اندازه هم بیشتر شود. ولی به طور همزمان، نیروی درگ بزرگی هم ایجاد شده است. همین موضوع، استفاده مثبت از نیروی لیفت را با پیچیدگی مواجه می‌کند.
برای یک ایرفویل معمولی که به جلو حرکت می کند ، اختلاف فشار یک جز a جریان را ایجاد می کند. به سمت بالا به عقب ، در عقب به پایین ، به سمت جلو در زیر و به سمت بالا به دور لبه جلو بروید. این گردش خون بازخورد مثبتی ایجاد می کند که در مقایسه با صفحه صاف چندین برابر افزایش می یابد. هرچه سریعتر پرواز کنید ، تأثیر آن بیشتر است.
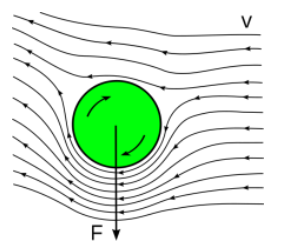
یک روتور در حال چرخش گردش خاص خود را از طریق اصطکاک در سراسر لایه مرزی ایجاد می کند. برای ایجاد و بزرگنمایی اثر برنولی ، منحرف کردن مقدار قابل توجهی هوا به سمت پایین و در واکنش نیوتونی به آن ، نیاز به بالابری مفید است که فقط باید به نسبت آهسته به جلو حرکت کند. این اثر مگنوس است.همانطور که در شکل نشان داده شده است ، سطح آب در یک سطل چرخان در نهایت مقعر خواهد شد. هرچه سرعت چرخش بیشتر باشد سطح آب مقعر بیشتری دارد. سطل موجود در تصویر سمت چپ خیلی سریع نمی چرخد ، بنابراین سطح آب خیلی مقعر نیست. سطل موجود در تصویر سمت راست بسیار سریع می چرخد ، بنابراین سطح آب بسیار مقعر است. نتیجه گیری: هرچه آب سریعتر بچرخد ، فشار در مرکز سطل کاهش می یابد.
همانطور که در شکل نشان داده شده است ، زیرا جریان هوا در سمت راست توپ در خلاف جهت چرخش توپ است ، جریان هوا در سمت راست توپ به آرامی می چرخد. جریان هوا در سمت چپ توپ در همان جهتی که جهت چرخش توپ وجود دارد می چرخد ، بنابراین جریان هوا در سمت چپ توپ سریع می چرخد. طبق نتیجه گیری در مورد سطل ، فشار در سمت چپ توپ باید کمتر از فشار در سمت راست توپ باشد. بنابراین توپ یک نیروی راست به چپ F اعمال خواهد شد.
جهت نیروی مگنوس
جهت نیرو توسط قضیه برنولی تعیین می شود. اگر بخواهم به طور خلاصه توضیح دهم قضیه برنولی نشان می دهد که در یک سیال، اگر یک ناحیه از سیال انرژی جنبشی بیشتری نسبت به دیگری داشته باشد، فشار اولی نسبت به دومی کمتر است (اگر ناحیه در همان سطح باشد، یعنی انرژی گرانشی وجود نداشته باشد و فشار اتمسفر ثابت است). بنابراین می بینید که در شکل ناحیه بالایی هوا به دلیل نیروی اصطکاک وارد شده توسط توپ به هوا در مقایسه با ناحیه پایین تر سریعتر خواهد بود. این بدان معناست که ناحیه بالا فشار کمتری نسبت به قسمت پایین دارد. ما می دانیم که سیال تمایل دارد از ناحیه فشار بالاتر به ناحیه پایین تر حرکت کند و به همین دلیل است که سیال به توپ فشار رو به بالا وارد می کند.
منشا چرخش و جهت در اثر مگنوس
اگر معادله برنولی را حل کنید:
$p=p_0-\rho_0{v^2 \over 2}$
با استفاده از یک پتانسیل جریان پیچیده برای جریان در اطراف یک استوانه:
$W(z)=v_0 z + {v_0 R^2 \over z} - {\Gamma \over 2 \pi } \ln(z)$
شما نیروهای بر طول $\vec f$ را با استفاده از یک انتگرال بر فشار $\vec f = - \int_{\text Cr} p \;\vec n ds$ که$F_x=0$ و $F_y=\rho_0 \Gamma v_0$را به دست می‌آورید.
1) آیا جهت نیرو در این مشکل متقارن از جهت گردش ناشی می شود؟
2) در تمام تصاویر مانند این استوانه در حال چرخش است چرا اینطور است؟ آیا به این دلیل است که کشیدن یک گردش سخت است،hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering
رهام حسامی ترم ششم مهندسی هوافضا
ا
