نیروی خالص از طریق مرکز ثقل (بدون گشتاور خالص) صرفاً یک جسم صلب (هر نقطه ای از بدن) را ترجمه می کند.
گشتاور خالص در هر نقطه از بدن (بدون نیروی خالص) صرفاً یک جسم صلب را حول مرکز ثقلش میچرخاند.
با وجود این موضوع، چگونه می توانم مرکز چرخش چند ضلعی با مرکز جرم C، نیروی F، و نقطه ای که در آن نیرو اعمال می شود A پیدا کنم؟ همچنین چه مقدار از نیرو به نیروی انتقالی و چه مقدار از آن به نیروی چرخشی تبدیل می شود؟ وقتی بیش از یک نیرو وجود دارد چگونه نیروها جمع می شوند؟
یک راه نیمه هندسی آسان برای یافتن مرکز چرخش در اثر یک نیرو وجود دارد.
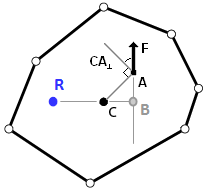
بازوی گشتاور c نیروی عبوری از A را پیدا کنید.
$c = r \cos \theta$
شعاع چرخش مرکز جرم C را پیدا کنید
$\rho = \sqrt{ \frac{I_C}{m} }$
فاصله ℓ از مرکز جرم را اندازه بگیرید و نقطه R را علامت بزنید
$\ell = \frac{\rho^2}{c}$
نقطه R مرکز نمونه چرخش است.
تخته ای به طول a و و عرض b با نیروی F به یک طرف آن زده می شود. یک سیستم مختصات را در مرکز جرم قرار دهید و بازوی گشتاور نیرو را به صورت $c=\frac{a}{2}$ اندازه بگیرید. گشتاور جرمی اینرسی یک تخته است
$I_C = \frac{m}{12} \left( a^2+b^2\right)$
و از این رو شعاع چرخش در اطراف مرکز است
$\rho = \sqrt{ \frac{a^2+b^2}{12} }$
مثال
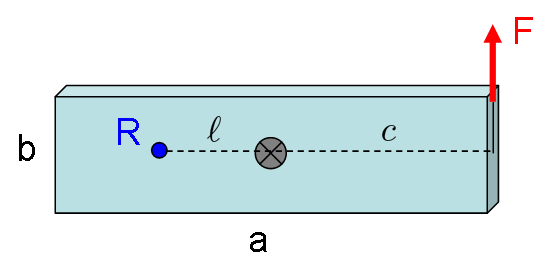
با روش بالا مرکز چرخش در یک فاصله است
$\boxed{\ell = \frac{\rho^2}{c} = \frac{ \frac{a^2+b^2}{12} } {\frac{a}{2} } = \frac{a^2+b^2}{6 a} }$
بیایید با استفاده از معادلات حرکت همان پاسخ را پیدا کنیم.
مجموع نیروهای جسم هستند
$\sum \boldsymbol{F} = (0,F,0)$
مجموع لحظه در مورد مرکز هستند
$\sum \boldsymbol{M} = (0,0,\frac{a}{2} F)$
شتاب خطی مرکز است
$\boldsymbol{a} = \frac{\sum \boldsymbol{F}}{m} = (0,\frac{F}{m},0)$
شتاب زاویه ای بدن است
$\boldsymbol{\alpha} = \frac{\sum \boldsymbol{M}}{I_C} = (0,0,\frac{6 F a}{m (a^2+b^2)})$
مرکز چرخش R را طوری بیابید که$\boldsymbol{a}_y=\ell \boldsymbol{\alpha}_z$ باشد
$\boxed{\ell = \frac{ \frac{F}{m} }{ \frac{6 F a}{m (a^2+b^2)} } = \frac{a^2+b^2}{6 a}}$
همان پاسخ!! برای بدست آوردن مرکز چرخش نیازی به انجام معادلات حرکت نیست. نقطه صرفاً نتیجه خواص اینرسی و هندسه است.
من فکر می کنم آنچه شما در مورد آن می پرسید با قضیه اساسی در مکانیک اجسام صلب پاسخ داده می شود، که بیان می کند که حرکت هر جسم صلب را می توان به حرکت مرکز جرم آن (نه لزوماً مستطیل) و چرخش حول آن تجزیه کرد. مرکز جرم (COM). دو جمله ای که شما تأکید می کنید پیامدهای مستقیم هستند. لطفا جزئیات را در لینک پیشنهادی یا هر متنی در مورد موضوع مشاهده کنید.
با این حال، ایده این نیست که یک مرکز ذاتی چرخش وجود دارد که گاهی اوقات با مرکز جرم منطبق می شود، یا اینکه ما لزوماً نیروهای وارد بر جسم را به اجزایی تجزیه می کنیم که COM را ترجمه می کند و دیگری که گشتاور را در مورد COM ایجاد می کند. . درست است که معادلات حرکت وقتی به این شکل بیان می شوند ساده ترین شکل را به دست می آورند.
بنابراین، برای پاسخ مستقیم به سوالاتم
چگونه می توانم مرکز چرخش یک چند ضلعی را زمانی که مرکز جرم (C)، نیرو (F) و نقطه اعمال نیرو (A) است، پیدا کنم؟
مرکز چرخش را به عنوان (C) در نظر بگیرید، صرف نظر از اینکه نیرو در کجا اعمال می شود.
همچنین چه مقدار از نیرو به نیروی انتقالی و چه مقدار از آن به نیروی چرخشی تبدیل می شود؟
همه آن، در هر دو مورد. معادلات حرکت برای COM چند ضلعی مسطح شما درست است
$M \vec{a} = \vec{F}\\
I\alpha \vec{k} = \vec{T}$
که در آن M جرم چند ضلعی کل است، $\vec{a}$ شتاب خطی COM (و جسم صلب)، I ممان اینرسی نسبت به COM، α شتاب زاویه ای در مورد COM، $\vec{k}$ بردار واحد نرمال است. به صفحه چند ضلعی، و$\vec{T}$ گشتاور $\vec{F}$ در مورد COM است. در 3D معادله گشتاور شامل یک عبارت اضافی در سمت چپ است.
وقتی بیش از یک نیرو وجود دارد چگونه نیروها جمع می شوند؟
مثل همیشه بردار. نیروی کل مجموع بردار نیروهای منفرد است و برای 2 بعدی گشتاور کل مجموع گشتاورهای مجزا در مورد COM یا گشتاور کل نیرو در مورد COM است، هر کدام که شما ترجیح می دهید..hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



