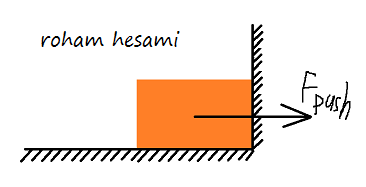
من می دانم که طبق قانون سوم نیوتن ، یک نیروی مخالف "واکنش" (بیایید بگوییم Freact) از دیوار متناسب با نیرویی که بلوک با دیوار فشار می دهد وجود خواهد داشت. اما چگونه باید نیروهای اصطکاک را در اینجا حساب کنم؟ باید اصطکاک حرکتی باشد یا ایستا؟ از آنجا که بلوک در حال حرکت نیست ، باید اصطکاک ساکن را حساب کنم؟ اما F_push در حال حاضر بیشتر از حداکثر نیروی اصطکاک ثابت Fs ، حداکثر بود. بنابراین اصطکاک حرکتی باید وارد عمل شود؟ اما جعبه تکان نمی خورد ...
یا باید روش دیگری داشته باشم؟ مانند ، از آنجا که بلوک به دیوار "چسبیده" است ، بخشی از آن می شود. بنابراین فشار دادن بلوک یعنی فشار دادن دیوار؟ بنابراین هیچ اصطکاک نیروهای افقی وجود ندارد؟
اصطکاک ایستا می تواند در وضعیت نهایی نشان داده شده توسط شما متفاوت باشد ، اصطکاک ایستا اصطکاک را محدود می کند و با اعمال نیروی خارجی مدام تغییر می کند تا زمانی که به حداکثر مقدار برسد
اکنون در وضعیت نهایی نیروی عادی از دیواره عمودی Nw برابر Fpush خواهد بود (همانطور که نشان دادید) ، بنابراین هیچ معادله خالصی برای تعادل برای نیروهای در وضعیت نهایی وجود ندارد ----
$Fpush = Nw + Fs ------- 1 (Fs$ نیروی اصطکاک است و به دلیل استراحت بلوک ، ایستا است اما نمی توان گفت $\mu sN$ نیروی طبیعی آن طبق طبقه است} ، زیرا اگر خالص نیستیم ، نیرو آنقدر زیاد است که به حداکثر اصطکاک ایستا نیاز دارد {متغیر آن با اعمال نیرو} هیچ اصطکاک حرکتی در نظر گرفته نمی شود ، زیرا حرکتی وجود ندارد.
توجه - معادله 1 برای تعادل افقی است ، همان است که می توانید برای جهت عمودی نیز استخراج کنید
نمودار بدنه بلوک را رسم کنید. شما به طور پیش فرض ، وزن و نیروی واکنش از زمین تعادل عمودی خواهید داشت. اکنون افقی را در نظر بگیرید.$F = f + R $
جایی که F نیروی فشار آور شماست. از آنجا که هیچ حرکت نسبی وجود ندارد ، این اصطکاک باید ماهیت ساکن داشته باشد.
به خاطر داشته باشید ، ما بدون دانستن F از مقدار اصطکاک اطلاع نداریم. اگر F بیشتر از fs (حداکثر) باشد ، نیروی اصطکاک در حداکثر مقدار خود خواهد بود.
یک بلوک در یک براکت روی یک سطح
بگویید یک بلوک (m1 = 10 کیلوگرم) در بالای یک براکت قرار دارد (m2 = 5.0 کیلوگرم) ، که براکت روی یک سطح بدون اصطکاک نشسته است. تصویر
 . ضرایب اصطکاک ثابت و جنبشی در نظر گرفته شده است: μs = 0.40 و μk = 0.30.سوال این است که حداکثر نیروی F که می تواند بدون کشیدن بلوک بر روی براکت اعمال شود چیست و شتاب a مربوط به براکت چقدر است؟$f_{s,max} = - \mu_sF_n = -\mu_s m_1 g$و$F = -f_{s,max} = \mu_sm_1g$و همچنین $F=m_{total}a = (m_1 + m_2)a$و$\mu_sm_1g = (m_1 + m_2)a$و$a = \frac{0.40\times 10.0 \times 9.81}{10.0 + 5.0} = 2.616 \text{ m/s}^2$
. ضرایب اصطکاک ثابت و جنبشی در نظر گرفته شده است: μs = 0.40 و μk = 0.30.سوال این است که حداکثر نیروی F که می تواند بدون کشیدن بلوک بر روی براکت اعمال شود چیست و شتاب a مربوط به براکت چقدر است؟$f_{s,max} = - \mu_sF_n = -\mu_s m_1 g$و$F = -f_{s,max} = \mu_sm_1g$و همچنین $F=m_{total}a = (m_1 + m_2)a$و$\mu_sm_1g = (m_1 + m_2)a$و$a = \frac{0.40\times 10.0 \times 9.81}{10.0 + 5.0} = 2.616 \text{ m/s}^2$هر جا که نیروی F (افقی فرض شده) اعمال شود حداکثر نیروی اصطکاک ساکن که بر دو بلوک وارد می شود$\mu_s m_1g$ است.
این حداکثر نیروی اصطکاک ایستا باعث تسریع در بلوک بالا یا تسریع در بلوک پایین می شود (نه هر دو بلوک به یک باره همانطور که در راه حل خود دارید) و نیروی اصطکاک مانع از تسریع بلوک دیگر خواهد شد که نیروی F بر آن وارد می شود.hope I help you I hope I help you understand the question. Roham Hesami


