مزیت مکانیکی یک قرقره متحرک 2 است. این بدان معناست که یک قرقره متحرک نیروی مورد نیاز برای حرکت هر جسم متصل به آن را به نصف کاهش می دهد. این اتفاق می افتد زیرا در یک قرقره متحرک یک انتهای طناب ثابت است ، به این معنی که مقداری از نیروی لازم برای حرکت جسم را جذب می کند
کششی که روی طنابهایی با چندین قرقره کار می کند
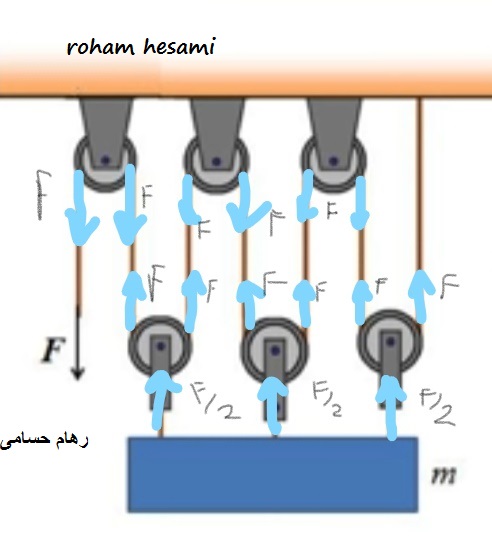
سوال من مربوط به مشکلی نیست که در تکالیف داده شده است ، بلکه کاملاً مفهومی است ، به همین دلیل فکر کردم که آن را اینجا بگذارم. در این عکس ، من F = T را می شناسم
جایی که T تنش است ، اما ظاهراً قانون دوم نیوتن در مورد توده اعمال شده است:
$ mg-6F=0$
تنها مسئله من مربوط به 6F است ، زیرا من فکر کردم که هر بار که از یکی از 3 قرقره تحتانی عبور می کند نیروها بر 2 تقسیم می شوند ، از این رو در ابتدا فکر کردم که باید
$ mg-(\frac{F}{2}+\frac{F}{4}+\frac{F}{8})=0$
همانطور که هر بار نیرو از طریق قرقره های تحتانی عبور می کند ، به 2 تقسیم می شود ، اما اینطور نیست ، چرا؟
مشکل این است که شما در حال مخلوط کردن ایده هستید. قرقره ها کل تلاش را آسان می کنند ، اما این بدان معنا نیست که هر طناب جدا از فاکتور 2 نسبت به سیم قبلی کاهش یابد. این اثر خالص چیزی است که مشاهده می کنید.
اما ، به طور کلی ، قبل از حل یک سیستم نباید تصور کنید که چگونه یک سیستم کار می کند. به همین دلیل شما می خواهید آن را sovle کنید؛ زیرا می خواهید آنچه را که واقعاً اتفاق می افتد بررسی کنید ، به جای آنچه فکر می کنید اتفاق می افتد ...
اول از همه ، شما نباید چیزی متفاوت از ابتدایی ترین ایده ها را تصور کنید. آنچه شما واقعاً دارید
نیروی کششی به صورت جفت به نظر می رسد: موردی که در انتهای قسمت اول طناب قرار دارد همان است که در انتهای قسمت دوم طناب قرار دارد. این به دلیل قانون سوم نیوتن است: تنش به صورت جفتی ظاهر می شود.
بنابراین ، اگر سرحال هستید ، چیزی شبیه به آن می نویسید
همانطور که مطمئن هستید هر قسمت طناب دارای دو نیروی کششی برابر و مخالف است. اما شما هیچ چیز دیگری نمی دانید
سپس ، اطلاعات بیشتری اضافه می کنیم. اگر یک قرقره فاقد جرم و اصطکاک باشد ، در این صورت می توانید مطمئن باشید که کشش دو طرف یکسان است. این به دلیل معادلات گشتاور است.
اگر مطمئن هستید که قرقره های بدون جرم دارید ، پس می توانید از این امر مطمئن باشید
$T_1=T_2=T_3=T_4=T_5=T6$
اما اگر پولی ها جرم داشته باشند ، این امر صحیح نیست.
سپس ، شما مرتباً محاسبه می کنید. با ترسیم نمودار بدن رایگان ادامه دهید.
برای خود توده ، شما دارید
$ T_A+T_B+T_C-mg=ma$
اگر وزن ثابت است ، a = 0 است
و نیروها جبران می شوند.
$ T_A+T_B+T_C=mg$
این همان چیزی است که شما می توانید از قوانین نیوتن استنباط کنید. شما هیچ چیز دیگری از آنها نمی دانید.
این معادله در مورد ترجمه صحبت می کند. البته اگر نیروهای رو به بالا وزن رو به پایین را جبران کنند ، وزن حرکت نمی کند ...
اما اگر می خواهید از $ T_A, T_B,T_C$چیزهای بیشتری بدانید
، شما به اطلاعات در مورد چرخش ها نیاز دارید. اگر بدن نچرخد ، به $ T_A = T_C $و غیره نیاز دارید.
به طور خلاصه ، هرگز آنچه اتفاق می افتد را تصور نکنید. هنگام افزودن اطلاعات سرحال باشید. هر تعداد ناشناخته را بیان کنید ، به محض یافتن معادلات جدید ، آنها را کاهش می دهید
تقسیم نیرویی قرقره های متحرک؟بنابراین در داخل یک سیم / رشته یک خاصیت به نام کشش وجود دارد که اندازه گیری نیرویی است که در امتداد رشته اعمال می شود. اگر رشته به طور همگن کشیده شود (در تمام قسمتهای رشته یکسان است) پس معلوم می شود که این کشش در تمام قسمتهای رشته یکسان است: شما با نیروی m نیوتن را می کشید ، سپس هر جا رشته ای را که باید فکر کنید می بینید آن را به عنوان یک نیروی mنیوتن
قرقره ها ، چون کاملاً "غلت می خورند" ، باعث می شوند کشش بین دو طرف رشته به همان مقدار برسد. (به عبارت دیگر ، اگر عدم تعادل کششی وجود داشته باشد ، طناب را در یک جهت می کشد ، بنابراین طناب فقط از طریق کشش پایین به بالا در امتداد چرخ قرقره می چرخد. این باعث کشش سمت کم فشار می شود و طرف فشار بالا را شل کنید ، اختلاف کشش را به 0 نزدیک کنید ، تا اختلاف تنش 0 شود و هر دو کشش یکسانی داشته باشند.)
به همین دلیل ، به سادگی مشاهده چرخ بزرگی که در هوا معلق است و تعادل نیرو در آن انجام می شود. با این وزن 450 N و گرانش خود 30 N به سمت پایین کشیده می شود. توسط 3T به سمت بالا کشیده می شود

جایی که T نیروی کشش درون رشته است. و T = F مطابق نمودار ، بنابراین 3T = 480 N یا
F = T = 160 N
قرقره متحرک چرخشی من سعی می کنم درک کنم که چگونه یک قرقره متحرک با جرم m و شعاع r
، که می چرخد و نمی لغزد در واقع کار می کند.
، اگر نیرویی در انتهای آزاد طناب وارد شود ، آیا معادلات زیر معتبر هستند؟
$ \begin{cases} F+T_1+T_2=m \frac{a}{2} \\ (T_1-T_2) r=I \alpha=I \frac{a}{r} \end{cases}$
جایی که I لحظه اینرسی دیسک هستم.
اگر از من بخواهند تنش های طناب و شتاب را تعیین کنم ، چگونه می توانم کار کنم؟ آیا اطلاعات کافی برای انجام آن را دارم؟
بگذارید T کششی در قسمت طناب باشد که به سقف یا سقف بسته شده است. سپس کشش در سمت نیروی اعمال شده طناب F است
2 شتاب وجود دارد: در
شتاب مماس طناب همانطور که باعث ایجاد و قطع تماس با قرقره می شود و شتاب عمودی قرقره است. بنابراین 3 ناشناخته وجود دارد: کشش T در طناب ، در و ay. آنها را می توان از نظر جرم پولی m و نیروی وارد شده F بدست آورد
ما به 3 معادله نیاز داریم:
$F + T –m*g = m*a_y$
(1)
$ (F-T)*r = I*\alpha = \frac {m*r^2*a_t} {2*r}$
(2)
$ a_y = \frac {a_t} {2}$
(3)
حل برای T$ T, a_t, a_y$
می دهد:
$T = \frac {m*g} {2}, a_t = \frac {(2*F – m*g)} {m}, a_y = \frac {(2*F – m*g)} {2*m}$
اگر نیروی اعمال شده F
برابر است ب$ \frac {m*g}{2}$
، هیچ شتابی از قرقره وجود ندارد.
این تنها راه حلی است که برای من منطقی است..i hope i helped roham hesami


