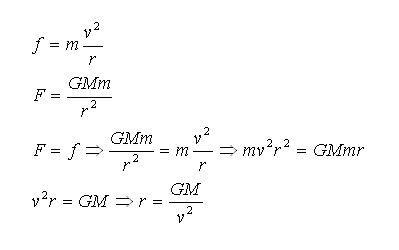
همانطور که میدانیم در معادلات فوق f نیروی جانب مرکز (گریزازمرکز، مرکزگرا) پرتابه یا سیاره، m جرم پرتابه یا سیاره، v سرعت خطی پرتابه یا سیاره روی مدار، r شعاع مدار يا فاصله پرتابه یا سیاره از مرکز میدان جاذبه (سیاره یا خورشید) ، F نیروی جاذبه مابین مرکز جاذبه یا خورشید با پرتابه یا سیاره، G ثابت جهانی گرانش، M جرم مرکز گرانش ( سیاره یا خورشید) است. اینک برای اینکه پرتابه یا سیاره بهدور مرکز جاذبه چرخش دایمی داشته باشد، میبایست F=f شود ، كه دراینرابطه فاصله r و سرعت v قابل محاسبه خواهد بود. لازم به توضیح است که نیوتن در آزمایشگاه خود با استفاده از یک وزنه و ریسمان به این نتیجه رسیده بود و بههرحال معادلات او معتبر هستند و در محاسبات عملاً جواب میدهند.
v=ωr
که ω همان سرعت زاویهای ( رادیان بر ثانیه - 2pi/s ) است:
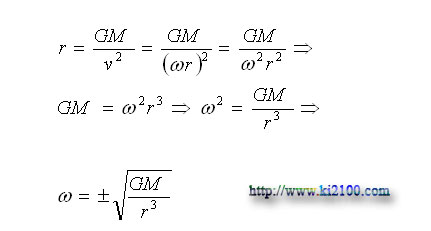
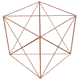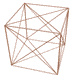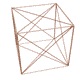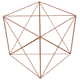
در ادامه مبحث برتری میدان برداری گرانش نیوتنی اینک میدان برداری خود را طرح میکنیم:

که یک سال مریخ ۱٫۸۸ برابر سال زمین و ۶۸۷ شبانهروز ماست.

اینک این میدان برداری را رسم میکنیم:
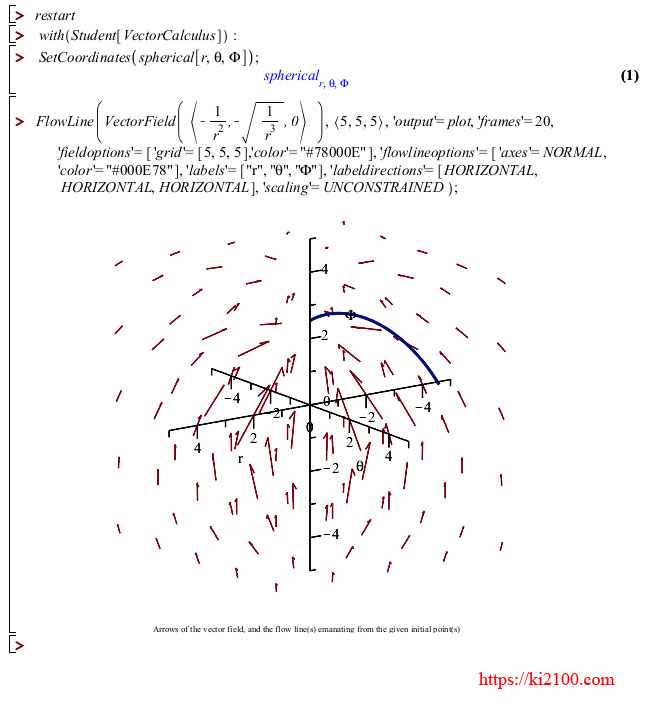
که بیانگر این واقعیت است که خود بردار نیرو و یا میدان برداری گرانش خمیده و انحنا پیدا میکند و نه چیز دیگری به نام فضا - زمان و نظریه انحنای فضا - زمان در نسبیت عام صرفاً یک مدل ریاضی برای توجیه پدیدههای فیزیکی است.
محمدرضا طباطباي