برای به دست آوردن فاصله L1، کوچکترین مقدار r را به گونه ای پیدا کنید که$\frac{M_2}{r_1^2} + \frac{M_1}{R^2} - \frac{r_1(M_1+M_2)}{R^3} - \frac{M_1}{(R-r_1)^2} = 0.$
برای به دست آوردن فاصله L2، کوچکترین مقدار r را به گونه ای بیابید که $\frac{M_1}{R^2} + \frac{r_2(M_1+M_2)}{R^3} - \frac{M_1}{(R+r_2)^2} - \frac{M_2}{r_2^2} = 0.$
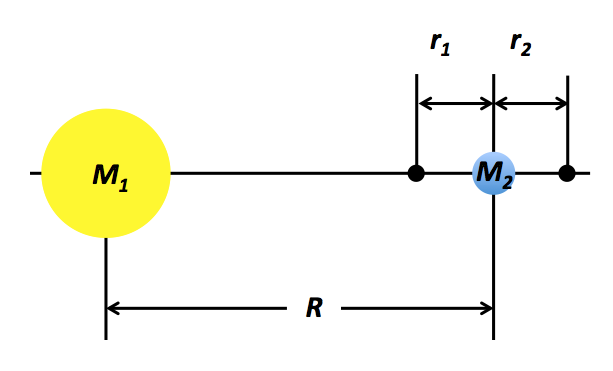
در بالا نحوه محاسبه فاصله از M2 تا نقاط L1 و L2 آمده است. این راه حل ها نشان دهنده تعادل بین نیروهای گرانشی و مرکزی در قاب هم چرخش هستند.
حال فرض کنید که جسم سوم یک نیروی مربع معکوس کاهش یافته از M1 توسط ضریب δ را تجربه کند که اگر فشار تشعشعی از خورشید را احساس کند ممکن است چنین باشد. نیروی M2 بدون تغییر خواهد بود اما از M1 با ضریب $1-\delta$مقیاس می شود.
سوالات:
آیا می توان نشان داد (به جای اینکه فقط گفته شود) که نقاط لاگرانژ هنوز وجود دارند و به همان شیوه رفتار می کنند، اما در مکان متفاوتی هستند؟
اگر آنها این کار را انجام دهند، معادله ای که باید برای r1 و r2 جدید برای δ داده شده حل شود چیست؟
"نقاط پاداش:" آیا می توان نشان داد (به جای اینکه فقط بیان شود) که مدارهای هاله همچنان وجود دارند و برای δ غیر صفر به روشی مشابه رفتار می کنند؟
نقطه آزادسازی را می توان به عنوان تعادل بین سه شتاب در یک چارچوب چرخشی مرجع دید.
جاذبه از M1جاذبه از M2شتاب گریز از مرکز.
برای L2، دو مورد اول به ترتیب$-\frac{(1 - \delta)M_1}{(R + r_2)^2}$ و $-\frac{M_2}{r_"^2}$ هستند. δ شما گنجانده شده است.
شتاب سوم $\omega^2r_{centre}$ خواهد بود که $\omega^2 = \frac{\mu}{R^3}$و $r_{centre} = \frac{RM_1}{\mu} + r_2 $
سپس داریم:$-\frac{M_2}{r_2^2} - \frac{(1 - \delta)M_1}{(R + r_2)^2} + \frac{M_1 + M_2}{R^3} \left(r_2 + \frac{RM_1}{M_1 + M_2}\right) = 0$که ساده می کند:$\frac{M_1}{R^2} + \frac{r_2(M_1 + M_2)}{R^3} - \frac{(1 - \delta)M_1}{(R + r_2)^2} -\frac{M_2}{r_2^2}= 0$
که بی تردید به فرمول دوم شما شباهت دارد.برای کامل بودن، L1 در اینجا آمده است:
$\frac{M_1}{R^2} + \frac{r_1(M_1 + M_2)}{R^3} - \frac{(1 - \delta)M_1}{(R + r_1)^2} +\frac{M_2}{r_1^2}= 0$
و L3:همچنین $-\frac{M_1}{R^2} - \frac{r_3(M_1 + M_2)}{R^3} + \frac{(1 - \delta)M_1}{(R + r_3)^2} +\frac{M_2}{r_3^2}= $این مشتق باید به 2 پاسخ دهد). اما آیا وجود دارد؟
برای آن می توان از استدلال بسیار ساده تری استفاده کرد.
فرض کنید L2 را به سمت داخل به سمت بدن دوم حرکت می کنیم:
گرانش M1 رشد می کند، اما فقط به سمت مقدار ثابت در فاصله جسم دوم.
گرانش M2 رشد می کند و با نزدیک شدن L2 به جرم نقطه ای، به سرعت به سمت بی نهایت می رود.
شتاب گریز از مرکز کاهش می یابد.
نتیجه این است که هر گونه افزایش در شتاب از M1 را می توان با مقدار زیاد دلخواه برای ترکیب دو شتاب دیگر مقابله کرد.
همین استدلال را می توان برای دور شدن از بدن دوم نیز مطرح کرد. شتاب گریز از مرکز به طور خطی به طور دلخواه بالا می رود، در حالی که گرانش مقابله با مجذور فاصله کوچک می شود تا زمانی که معادله به تعادل برسد.
L2 همیشه وجود داردبا این حال، این موضوع برای L1 صادق نیست. در حالی که افزایش شتاب از M1 را می توان با حرکت خودسرانه L1 در نزدیکی بدنه دوم مقابله کرد، کاهش در شتاب بیش از $1 - \delta = 0$ باعث می شود که تمام شتاب ها در یک جهت باشند. در واقع، فرد باید در طرف مقابل بدنه مرکزی باشد، در این صورت $L_2 \equiv L_3$.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



