سلام بچهها. میخواستم بدونم اگه $n$ یه عدد طبیعی باشه و $i$ یکّهی موهومی، در اون صورت آیا حد زیر درسته؟
$$\lim_{n \to +\infty}(\frac{n^2}{n^2+1}+i(\frac{n}{n^2+1}))=1$$
حد بی نهایت متغیر مختلط
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3265-
سپاس: 5494
- جنسیت:
تماس:
Re: حد بی نهایت متغیر مختلط
سوالت خیلی راحته به قول معروف مرغ پاک کرده هم میدونه
قضیه1میدونی دنباله دارای حد $z_n = x_n+iy_n → z = x+iy ⇔ x_n →x, y_n→y$ است اگر و فقط اگر دنباله های حقیقی همگرا باشن
تأیید اثباتم: یک دنباله مختلط همگرا محدودیت منحصر به فردی داره$\lim_{n \to +\infty}(\frac{n^2}{n^2+1}+i(\frac{n}{n^2+1}))=1$ فقط به صورت مجموع دو حد بنویس قسمت اول یک و دومی صفر میشه$\lim_{n \to +\infty}(\frac{n^2}{n^2+1}$
ببیمتن تو ریاضی مهندسی $\lim_{n \to \infty} lim_{} \left(\frac{n^{2}}{n^{2} + 1} + \frac{i n}{n^{2} + 1}\right) \left(i f n t y + n o t\right)$خیلی راحت میدونی $\lim_{n \to +\infty}i(\frac{n}{n^2+1})) $برابر صفر هست ببین $\lim_{n\to\infty} \sum_{k=1}^{n^2} \frac{n}{n^2+k^2}$میدونی که برای هر تابع نزولی $f:\mathbb{R}\to\mathbb{R}$ و هر N>1
ما داریم$\int\limits_1^{N+1}f(x)dx\leq \sum\limits_{k=1}^{N}f(k)\leq \int\limits_0^N f(x)dx$
بعد از تعویض $N=n^2$و$f(x)=n/(n^2+x^2)$
و محاسبات خیلی اسون $\arctan\frac{n^2+1}{n}-\arctan \frac{1}{n}\leq\sum\limits_{k=1}^{n^2}\frac{n}{n^2+k^2}\leq\arctan n$من اینجا برات یک حد $n\to\infty$ بگیرم
، سپس از لم ساندویچ استفاده کنم
$\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n^2}\frac{n}{n^2+k^2}=\frac{\pi}{2}$
تأیید اثبات: یک دنباله مختلط همگرا محدودیت منحصر به فردی دارد.دنباله ای از اعداد مختلط $\{w_n\}_{n=1}^{\infty}$
گفته میشه اگر w∈C وجود داشته باشه همگرا میشه به طوری که$\lim_{n\to\infty}|w_n-w|=0.$
اثبات کنین که یک دنباله همگرا از اعداد مختلط یک حد منحصر داره اثبات من اینطوره
اجازه بدین حد دنباله همگرا $\{w_n\}_{n=1}^{\infty}$ باشه غیر منحصر به فرد باشد و اجازه بدین $w'$ هر دو w همگرا بشه
و ما. سپس باید نشان دهم که $w'=w$
. من دارم$\lim_{n\to\infty}|w_n-w|=0$
و$\lim_{n\to\infty}|w_n-w'|=0.$اینجا |z| برای تمام $z\in\Bbb{C}$ واقعیه، می تونم از قضیه حد جبری برای نوشتن استفاده کنم
$\lim_{n\to\infty}|w_n-w|+\lim_{n\to\infty}|w_n-w'|=\lim_{n\to\infty}|w_n-w|+|w_n-w'|=0.$
حالا از نابرابری مثلث برای بدست آوردن استفاده کنین
$0=\lim_{n\to\infty}|w_n-w|+|w_n-w'|\geq\lim_{n\to\infty}|w_n-w+w_n-w'|=\lim_{n\to\infty}|2w_n-w-w'|$
و بنابراین ما$\lim_{n\to\infty}|w_n-\frac{w+w'}{2}|\leq 0$را دریافت می کنیم$\lim_{n\to\infty}|w_n-\frac{w+w'}{2}|=0$
. اما مقدار مطلق غیر منفیه، بنابراین و $\frac{w+w'}{2}$ همچنین حدی از دنباله $\{w_n\}_{n=1}^{\infty}$ است. بنابراین ما w داریم(یا $w'$$\frac{w+w'}{2}$ و بنابراین $w=w'$.
آیا این اثبات صحیح است؟ از آنجایی که من فرض می کنم دنباله$w'$ به w همگرا می شود
و w، فکر کنم آخرین جمله در اثبات معتبر است؟ آیا من در استدلالم اشتباه می کنم؟من راهی برای حل مستقیم این موضوع پیدا کرده ام، بدون اینکه به منحصر به فرد بودن محدودیت های $\operatorname{Re}(w_n)$ متوسل شوم.
و$\operatorname{Im}(w_n)$
بگذارید دنباله به دو حد مختلف همگرا شود، w و $w'$. سپس از تعریف داده شده همگرایی داریم$\lim_{n\to\infty}|w_n-w|=\lim_{n\to\infty}|w_n-w'|=0.$با استفاده از قضیه حد جبری$\lim f \pm g = \lim f \pm \lim g$
و نابرابری $|a-b|\geq |a|-|b|$ برایمقادیر a و b، ما داریم
$0=\lim_{n\to\infty}|w_n-w|-\lim_{n\to\infty}|w_n-w'|=\lim_{n\to\infty}|w_n-w|-|w_n-w'|\leq\lim_{n\to\infty}|w_n-w-w_n+w'|$که از آن می گیریم $|w'-w|\geq 0$
. همچنین با استفاده از نابرابری مثلث،$0=\lim_{n\to\infty}|w_n-w|+\lim_{n\to\infty}|w_n-w'|=\lim_{n\to\infty}|w_n-w|+\lim_{n\to\infty}|w'-w_n|\geq\lim_{n\to\infty}|w_n-w+w'-w_n|$که از آن می گیرم $|w'-w|\leq 0.$.
بنابراین، باید$|w'-w|=0$ داشته باشیم و از این رو $w′=w$
همگرایی دنباله ها
یک دنباله بی نهایت $\left\{z_1,z_2,z_3 \ldots\right\}$
اعداد مختلط دارای حد z است اگر برای هر عدد مثبت ε، یک عدد صحیح مثبت $n_0$ وجود داره به طوری که
$\left|z_n-z\right|< \varepsilon \quad \text{whenever}\quad n > n_0.$
از نظر هندسی، این بدان معنیه که برای مقادیر به اندازه کافی بزرگ n، نقاط $z_n$
در هر ε داده شده برای z از آنجایی که می تونیم ε را انتخاب کنیم به هر اندازه که ما بخواهیم کوچکیه نتیجه این است که نقاط $z_n$ به طور دلخواه به z نزدیک شود با افزایش اشتراک آنها. توجه داشته باشید که مقدار $n_0$
که مورد نیاز است، به طور کلی، به مقدار ε بستگی دارهتفسیر هندسی دنباله $\left\{z_n\right\}_{n=1}^{\infty}$
می تواند حداکثر یک محدودیت داشته باشد. یعنی یک حد z
در صورت وجود منحصر به فرد است. وقتی آن حد وجود داشته باشد، گفته میشه دنباله به z همگرا میشه
; و من می نویسم$\lim_{n\rightarrow \infty} z_n=z$
اگر دنباله محدودیتی نداشته باشه واگرا میشه قضیه 1: فرض کنید $z_n=x_n+iy_n$
$n=1,2,3,\ldots$) $z=x+iy$
. سپس$\lim_{n\rightarrow \infty} z_n=z$
اگر و تنها اگر$\lim_{n\rightarrow \infty} x_n=x\quad \text{and}\quad \lim_{n\rightarrow \infty} y_n=y.$
اثبات همگرایی سری یک سری بی نهایت $\sum_{n=1}^{\infty}z_n=z_1+z_2+z_3+\cdots$
اعداد مختلط به جمع S همگرامیشن
اگر دنباله$\sum_{n=1}^{N}z_n=z_1+z_2+z_3+\cdots +z_N\quad(N=1,2,3,\ldots)$
از مجموع جزئی به S همگرا میشه
; سپس می نویسم
$\sum_{n=1}^{\infty}z_n=S.$
توجه کن که از آنجایی که یک دنباله می تونه حداکثر یک حد داشته باشه یک سری می تونه حداکثر یک مجموع داشته باشه. وقتی یک سری همگرا نمیشهه میگم واگرا میشه .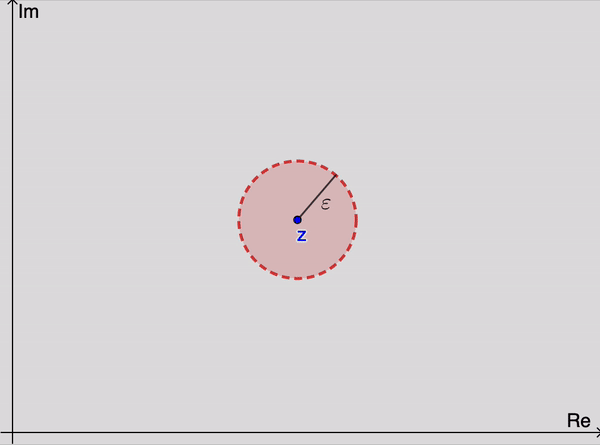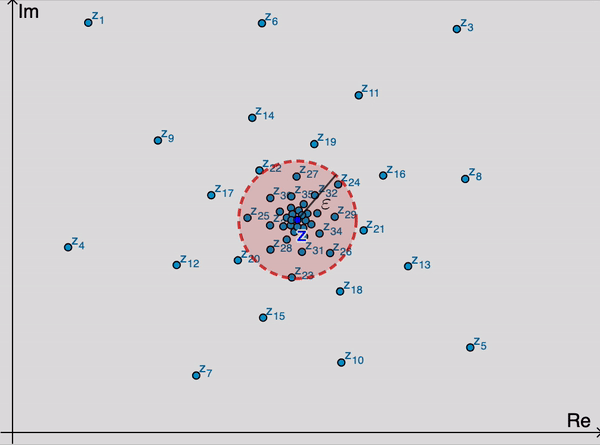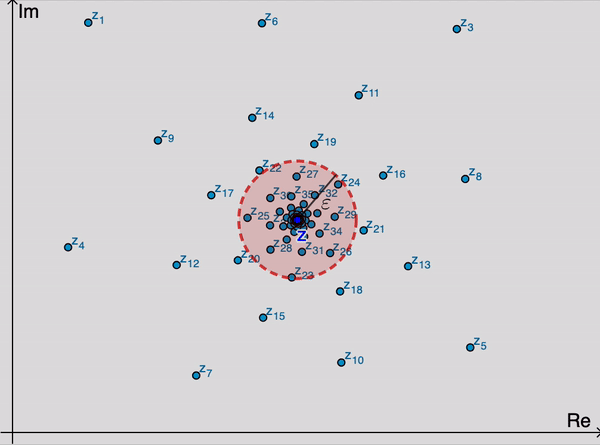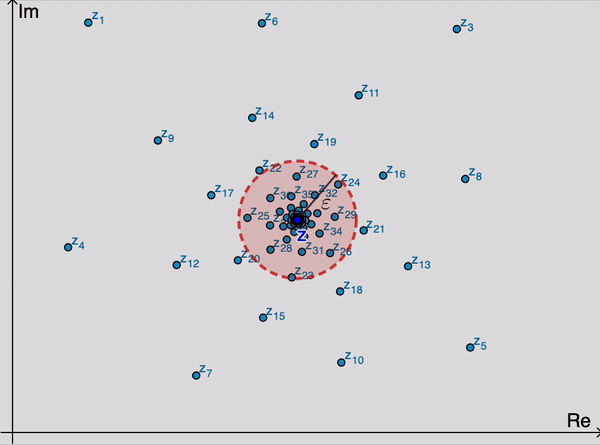
قضیه 2: فرض کنید $z_n=x_n+iy_n$
$n=1,2,3,\ldots$) و $S=X+iY$
. سپس $\sum_{n=1}^{\infty} z_n=S$
اگر و تنها اگر$\sum_{n=1}^{\infty} x_n=X\quad \text{and}\quad \sum_{n=1}^{\infty} y_n=Y.$
اگر یک سری اعداد مختلط همگرا بشن nجمله -ام به صورت n به صفر همگرا میشه به بی نهایت تمایل داره
از ویژگی نتیجه میگیرم که شرایط سریهای همگرا محدود هستن. یعنی زمانی که سری (4
) همگرا می شود، یک ثابت مثبت M وجود داره
به طوری که$|z_n| \leq M \; \text{ for each positive integer } n.$ برای هر عدد صحیح مثبت n.
یکی دیگر از ویژگی های مهم سری اعداد مختلط که از یک ویژگی متناظر در حساب دیفرانسیل و انتگرال پیدا میشه
خاصیت 2: همگرایی مطلق یک سری اعداد مختلط دلالت بر همگرایی آن سری داره
گر سری کاملاً همگرا باشه$\sum_{n=1}^{\infty}|z_n|=\sum_{n=1}^{\infty}\sqrt{x^2_n+y^2_n}\quad \quad(z_n=x_n+iy_n)$
از اعداد حقیقی$\sqrt{x^2_n+y^2_n}$ همگرا میشه .برای اثبات این واقعیت که مجموع یک سری یک عدد معین S است
، تعریف باقی مانده $\rho_N$اغلب راحت است
بعد از N شرایط، با استفاده از مجموع جزئی:$\rho_N=S-S_N$
بنابراین $S=S_N+\rho_N$
. اکنون، از آنجایی که $|S_N-S|=|\rho_N-0|$، سپس یک سری به عدد S همگرا میشه
اگر و فقط اگر دنباله باقیمانده ها به سمت صفر گرایش داشته باشه
با کمک باقیمانده هااثبات آن آسان است$\sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1$
ما فقط نیاز به یادآوری هویت داریم$1+z+z^2+\cdots+z^n=\frac{1-z^{n+1}}{1-z}$
برای نوشتن مقادیر جزئی
$S_N(z)=\sum_{n=0}^{\infty}z^n=1+z+z^2+\cdots+z^{N-1}\quad\quad(z\neq 1)$
مانند$S_N(z)=\frac{1-z^N}{1-z}.$
اگر$S(z)=\frac{1}{1-z}$
سپس
$\rho_N(z)=S(z)-S_N(z)=\frac{z^N}{1-z}\quad\quad(z\neq 1).$
بدین ترتیب$\left|\rho_N\right|=\frac{|z|^N}{|1-z|}\rightarrow 0\quad\text{only when}\quad |z|<1.$ وقتی$|z|<1.$
در این حالت مشخص است که باقی مانده $\rho_N$ وقتی$ |z|<1 $به صفر میل کنید
اما نه زمانی که $|z|\geq 1$
سری معرفی شده در مثال قبلی ام $\sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1$
به سری هندسی معروفه
قضیه1میدونی دنباله دارای حد $z_n = x_n+iy_n → z = x+iy ⇔ x_n →x, y_n→y$ است اگر و فقط اگر دنباله های حقیقی همگرا باشن
تأیید اثباتم: یک دنباله مختلط همگرا محدودیت منحصر به فردی داره$\lim_{n \to +\infty}(\frac{n^2}{n^2+1}+i(\frac{n}{n^2+1}))=1$ فقط به صورت مجموع دو حد بنویس قسمت اول یک و دومی صفر میشه$\lim_{n \to +\infty}(\frac{n^2}{n^2+1}$
ببیمتن تو ریاضی مهندسی $\lim_{n \to \infty} lim_{} \left(\frac{n^{2}}{n^{2} + 1} + \frac{i n}{n^{2} + 1}\right) \left(i f n t y + n o t\right)$خیلی راحت میدونی $\lim_{n \to +\infty}i(\frac{n}{n^2+1})) $برابر صفر هست ببین $\lim_{n\to\infty} \sum_{k=1}^{n^2} \frac{n}{n^2+k^2}$میدونی که برای هر تابع نزولی $f:\mathbb{R}\to\mathbb{R}$ و هر N>1
ما داریم$\int\limits_1^{N+1}f(x)dx\leq \sum\limits_{k=1}^{N}f(k)\leq \int\limits_0^N f(x)dx$
بعد از تعویض $N=n^2$و$f(x)=n/(n^2+x^2)$
و محاسبات خیلی اسون $\arctan\frac{n^2+1}{n}-\arctan \frac{1}{n}\leq\sum\limits_{k=1}^{n^2}\frac{n}{n^2+k^2}\leq\arctan n$من اینجا برات یک حد $n\to\infty$ بگیرم
، سپس از لم ساندویچ استفاده کنم
$\lim\limits_{n\to\infty}\sum\limits_{k=1}^{n^2}\frac{n}{n^2+k^2}=\frac{\pi}{2}$
تأیید اثبات: یک دنباله مختلط همگرا محدودیت منحصر به فردی دارد.دنباله ای از اعداد مختلط $\{w_n\}_{n=1}^{\infty}$
گفته میشه اگر w∈C وجود داشته باشه همگرا میشه به طوری که$\lim_{n\to\infty}|w_n-w|=0.$
اثبات کنین که یک دنباله همگرا از اعداد مختلط یک حد منحصر داره اثبات من اینطوره
اجازه بدین حد دنباله همگرا $\{w_n\}_{n=1}^{\infty}$ باشه غیر منحصر به فرد باشد و اجازه بدین $w'$ هر دو w همگرا بشه
و ما. سپس باید نشان دهم که $w'=w$
. من دارم$\lim_{n\to\infty}|w_n-w|=0$
و$\lim_{n\to\infty}|w_n-w'|=0.$اینجا |z| برای تمام $z\in\Bbb{C}$ واقعیه، می تونم از قضیه حد جبری برای نوشتن استفاده کنم
$\lim_{n\to\infty}|w_n-w|+\lim_{n\to\infty}|w_n-w'|=\lim_{n\to\infty}|w_n-w|+|w_n-w'|=0.$
حالا از نابرابری مثلث برای بدست آوردن استفاده کنین
$0=\lim_{n\to\infty}|w_n-w|+|w_n-w'|\geq\lim_{n\to\infty}|w_n-w+w_n-w'|=\lim_{n\to\infty}|2w_n-w-w'|$
و بنابراین ما$\lim_{n\to\infty}|w_n-\frac{w+w'}{2}|\leq 0$را دریافت می کنیم$\lim_{n\to\infty}|w_n-\frac{w+w'}{2}|=0$
. اما مقدار مطلق غیر منفیه، بنابراین و $\frac{w+w'}{2}$ همچنین حدی از دنباله $\{w_n\}_{n=1}^{\infty}$ است. بنابراین ما w داریم(یا $w'$$\frac{w+w'}{2}$ و بنابراین $w=w'$.
آیا این اثبات صحیح است؟ از آنجایی که من فرض می کنم دنباله$w'$ به w همگرا می شود
و w، فکر کنم آخرین جمله در اثبات معتبر است؟ آیا من در استدلالم اشتباه می کنم؟من راهی برای حل مستقیم این موضوع پیدا کرده ام، بدون اینکه به منحصر به فرد بودن محدودیت های $\operatorname{Re}(w_n)$ متوسل شوم.
و$\operatorname{Im}(w_n)$
بگذارید دنباله به دو حد مختلف همگرا شود، w و $w'$. سپس از تعریف داده شده همگرایی داریم$\lim_{n\to\infty}|w_n-w|=\lim_{n\to\infty}|w_n-w'|=0.$با استفاده از قضیه حد جبری$\lim f \pm g = \lim f \pm \lim g$
و نابرابری $|a-b|\geq |a|-|b|$ برایمقادیر a و b، ما داریم
$0=\lim_{n\to\infty}|w_n-w|-\lim_{n\to\infty}|w_n-w'|=\lim_{n\to\infty}|w_n-w|-|w_n-w'|\leq\lim_{n\to\infty}|w_n-w-w_n+w'|$که از آن می گیریم $|w'-w|\geq 0$
. همچنین با استفاده از نابرابری مثلث،$0=\lim_{n\to\infty}|w_n-w|+\lim_{n\to\infty}|w_n-w'|=\lim_{n\to\infty}|w_n-w|+\lim_{n\to\infty}|w'-w_n|\geq\lim_{n\to\infty}|w_n-w+w'-w_n|$که از آن می گیرم $|w'-w|\leq 0.$.
بنابراین، باید$|w'-w|=0$ داشته باشیم و از این رو $w′=w$
همگرایی دنباله ها
یک دنباله بی نهایت $\left\{z_1,z_2,z_3 \ldots\right\}$
اعداد مختلط دارای حد z است اگر برای هر عدد مثبت ε، یک عدد صحیح مثبت $n_0$ وجود داره به طوری که
$\left|z_n-z\right|< \varepsilon \quad \text{whenever}\quad n > n_0.$
از نظر هندسی، این بدان معنیه که برای مقادیر به اندازه کافی بزرگ n، نقاط $z_n$
در هر ε داده شده برای z از آنجایی که می تونیم ε را انتخاب کنیم به هر اندازه که ما بخواهیم کوچکیه نتیجه این است که نقاط $z_n$ به طور دلخواه به z نزدیک شود با افزایش اشتراک آنها. توجه داشته باشید که مقدار $n_0$
که مورد نیاز است، به طور کلی، به مقدار ε بستگی دارهتفسیر هندسی دنباله $\left\{z_n\right\}_{n=1}^{\infty}$
می تواند حداکثر یک محدودیت داشته باشد. یعنی یک حد z
در صورت وجود منحصر به فرد است. وقتی آن حد وجود داشته باشد، گفته میشه دنباله به z همگرا میشه
; و من می نویسم$\lim_{n\rightarrow \infty} z_n=z$
اگر دنباله محدودیتی نداشته باشه واگرا میشه قضیه 1: فرض کنید $z_n=x_n+iy_n$
$n=1,2,3,\ldots$) $z=x+iy$
. سپس$\lim_{n\rightarrow \infty} z_n=z$
اگر و تنها اگر$\lim_{n\rightarrow \infty} x_n=x\quad \text{and}\quad \lim_{n\rightarrow \infty} y_n=y.$
اثبات همگرایی سری یک سری بی نهایت $\sum_{n=1}^{\infty}z_n=z_1+z_2+z_3+\cdots$
اعداد مختلط به جمع S همگرامیشن
اگر دنباله$\sum_{n=1}^{N}z_n=z_1+z_2+z_3+\cdots +z_N\quad(N=1,2,3,\ldots)$
از مجموع جزئی به S همگرا میشه
; سپس می نویسم
$\sum_{n=1}^{\infty}z_n=S.$
توجه کن که از آنجایی که یک دنباله می تونه حداکثر یک حد داشته باشه یک سری می تونه حداکثر یک مجموع داشته باشه. وقتی یک سری همگرا نمیشهه میگم واگرا میشه .

قضیه 2: فرض کنید $z_n=x_n+iy_n$
$n=1,2,3,\ldots$) و $S=X+iY$
. سپس $\sum_{n=1}^{\infty} z_n=S$
اگر و تنها اگر$\sum_{n=1}^{\infty} x_n=X\quad \text{and}\quad \sum_{n=1}^{\infty} y_n=Y.$
اگر یک سری اعداد مختلط همگرا بشن nجمله -ام به صورت n به صفر همگرا میشه به بی نهایت تمایل داره
از ویژگی نتیجه میگیرم که شرایط سریهای همگرا محدود هستن. یعنی زمانی که سری (4
) همگرا می شود، یک ثابت مثبت M وجود داره
به طوری که$|z_n| \leq M \; \text{ for each positive integer } n.$ برای هر عدد صحیح مثبت n.
یکی دیگر از ویژگی های مهم سری اعداد مختلط که از یک ویژگی متناظر در حساب دیفرانسیل و انتگرال پیدا میشه
خاصیت 2: همگرایی مطلق یک سری اعداد مختلط دلالت بر همگرایی آن سری داره
گر سری کاملاً همگرا باشه$\sum_{n=1}^{\infty}|z_n|=\sum_{n=1}^{\infty}\sqrt{x^2_n+y^2_n}\quad \quad(z_n=x_n+iy_n)$
از اعداد حقیقی$\sqrt{x^2_n+y^2_n}$ همگرا میشه .برای اثبات این واقعیت که مجموع یک سری یک عدد معین S است
، تعریف باقی مانده $\rho_N$اغلب راحت است
بعد از N شرایط، با استفاده از مجموع جزئی:$\rho_N=S-S_N$
بنابراین $S=S_N+\rho_N$
. اکنون، از آنجایی که $|S_N-S|=|\rho_N-0|$، سپس یک سری به عدد S همگرا میشه
اگر و فقط اگر دنباله باقیمانده ها به سمت صفر گرایش داشته باشه
با کمک باقیمانده هااثبات آن آسان است$\sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1$
ما فقط نیاز به یادآوری هویت داریم$1+z+z^2+\cdots+z^n=\frac{1-z^{n+1}}{1-z}$
برای نوشتن مقادیر جزئی
$S_N(z)=\sum_{n=0}^{\infty}z^n=1+z+z^2+\cdots+z^{N-1}\quad\quad(z\neq 1)$
مانند$S_N(z)=\frac{1-z^N}{1-z}.$
اگر$S(z)=\frac{1}{1-z}$
سپس
$\rho_N(z)=S(z)-S_N(z)=\frac{z^N}{1-z}\quad\quad(z\neq 1).$
بدین ترتیب$\left|\rho_N\right|=\frac{|z|^N}{|1-z|}\rightarrow 0\quad\text{only when}\quad |z|<1.$ وقتی$|z|<1.$
در این حالت مشخص است که باقی مانده $\rho_N$ وقتی$ |z|<1 $به صفر میل کنید
اما نه زمانی که $|z|\geq 1$
سری معرفی شده در مثال قبلی ام $\sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1$
به سری هندسی معروفه

Re: حد بی نهایت متغیر مختلط
خب حالا که اینقدر راحت بود بذار یه خورده سختترش کنیم. به نظرت این سری همگراست؟ میدونی حدودی به چه عددی میل میکنه؟
$$\sum_{n=1}^{\infty}Ln(\frac{ne^{1/n}}{n+1})$$
$$\sum_{n=1}^{\infty}Ln(\frac{ne^{1/n}}{n+1})$$
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3265-
سپاس: 5494
- جنسیت:
تماس:
Re: حد بی نهایت متغیر مختلط
جواب همگرا و حدش در بینهایت میشه صفر.
یکی از تست های بسیار قدرتمند ;که به آن اشاره شده تست گاوسه. در اینجا، اگر سری مثبت $\sum a_n$
به گونه ای ا که $\frac{a_n}{a_{n+1}} = 1+\frac{h}{n}+O(\frac{1}{n^\alpha}),$برای $\alpha>1$ سپس $\sum a_n$
اگر h>1 همگرا میشه و اگر h≤1 واگرا میشه
میدونیاست که $\sum a_n$ همگرا می شود اگر$a_n$ به اندازه کافی سریع به 0 میل میکنه
. راه دیگر برای نگاه کردن به آن این است که برای همه t>0 ایا$\lambda(t) = \left|\{n \geq 1 : a_n \geq t\}\right|$
از جمله های دنباله بزرگتر از t محدوده و خیلی سریع به +∞ تمایل ندارن به عنوان t به 0 تمایل داره.
$\boxed{\displaystyle\sum_{n\geq 1} a_n < \infty \iff \int_0^\infty \lambda(t)dt < \infty}$
ببین که اگر $\lim a_n = 0$ باشه، خوبه که یکپارچگی را فقط در (0,1) بررسی کنی
تست کوشی
که با حد بالایی $\lambda_n=\sqrt[n]{a_n}$ سروکار داره ، اما زمانی که حد بالایی 1 باشد به نتیجه نمی رسه
آزمون دالامبر
که با حد بالا یا پایین $\lambda_n=\frac{a_{n+1}}{a_n}$ سروکار داره
، اما زمانی که $ limit ≥1 $ باشد به نتیجه نمی رسه $ limit ≤1$
آزمون برتراند
که با $\lambda_n= (\ln n)\Big[n\Big(\frac{x_n}{x_{n+1}}-1\Big)-1\Big]$ سروکار دارد.
، اما هنوز وقتی $\lim\lambda_n=1$ به نتیجه نمیرسه
مثال من میگم $\sum\limits_{n = 1}^\infty {\large\frac{{{e^{\frac{1}{n}}}}}{{{n^2}}}\normalsize}$همگراست ببین ${e^{\large\frac{1}{n}\normalsize}} \le e$ازمون میزارم $\large {\sum\limits_{n = 1}^\infty {\frac{{{e^{\large\frac{1}{n}\normalsize}}}}{{{n^2}}}} }
\le {\sum\limits_{n = 1}^\infty {\frac{e}{{{n^2}}}} }
= {e\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} .}$خوب چون $\sum\limits_{n = 1}^\infty {\large\frac{1}{{{n^2}}}\normalsize}$همگراست پس سری اصلی همگراست
همیشه دالامبر هم جواب نمیده ها
دقت کن $\sum_{n=1}^{\infty}Ln(\frac{ne^{1/n}}{n+1}) = 0.577216$و $\sum_{n=1}^{\infty}Ln(\frac{ne^{1/n}}{n+1})converges$
اینم مرغ پاک کرده میدونه $L = \mathop {\lim }\limits_{n \to \infty } \left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right|$مثال من $L < 1$
بازم میگم بیایید نگاهی به $\sum_{k = 1}^{\infty} a_n$ بیندازیم
(جایی که $a_n \in \mathbb{R}$ یا $a_n \in \mathbb{C}$ برای هر n∈N دارم $\limsup_{n \rightarrow \infty} $
یعنی سری $\sum_{k = 1}^{\infty} a_n$ کاملاً همگرا میشه
$\lim_{n \rightarrow \infty} |\frac{a_{n+1}}{a_n}| > 1$یعنی سری $\sum_{k = 1}^{\infty} a_n$ واگرا میشه.
از هر آزمونی برای تعیین همگرایی سری $\sum_{n=1}^\infty \frac{(-1)^ne^{\frac{1}{n}}}{n^3}$استفاده کنید
آزمون مقایسه از طریق: $e^{1/n}\leq 3$ انجام میشه
بنابراین $\left|(-1)^{n}\dfrac{e^{1/n}}{n^{3}}\right|\leq\dfrac{3}{n^{3}}$
یک تست مقایسه محدود انجام دهید. اگر$b_n = \frac{1}{n^3}$ را انتخاب کنین
بعدش $\lim_{n \to \infty} \frac{a_n}{b_n} = \lim_{n \to \infty} e^{\frac{1}{n}} = 1 \gt0$
این بدان معنی است که هر دو $\sum a_n$
و $\sum b_n$ بر اساس همگرایی/واگرایی $\sum b_n$ یا همگرا یا واگرا میشه
.همانطور که من گفتم $\sum_{n=1}^\infty\frac{1}{n^3}$ یک سری p همگرا هستش و بنابراین با آزمایش مقایسه حدی سری اصلی من کاملاً همگراهست.
.ببین یک مثال از کتابم $\sum_{n= 1}^{\infty} \frac{(-1)^n\ln(n)}{n(n+1)} = 0.063254$
$\begin{align}\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n(n+1)}&=\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}n-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\\&=\frac d{dx}\sum_{n=1}^\infty\frac{(-1)^nn^x}n\bigg|_{x=0}-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\\&=\eta'(1)-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\\&=\gamma\ln(2)-\frac12[\ln(2)]^2-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\end{align}$

یکی از تست های بسیار قدرتمند ;که به آن اشاره شده تست گاوسه. در اینجا، اگر سری مثبت $\sum a_n$
به گونه ای ا که $\frac{a_n}{a_{n+1}} = 1+\frac{h}{n}+O(\frac{1}{n^\alpha}),$برای $\alpha>1$ سپس $\sum a_n$
اگر h>1 همگرا میشه و اگر h≤1 واگرا میشه
میدونیاست که $\sum a_n$ همگرا می شود اگر$a_n$ به اندازه کافی سریع به 0 میل میکنه
. راه دیگر برای نگاه کردن به آن این است که برای همه t>0 ایا$\lambda(t) = \left|\{n \geq 1 : a_n \geq t\}\right|$
از جمله های دنباله بزرگتر از t محدوده و خیلی سریع به +∞ تمایل ندارن به عنوان t به 0 تمایل داره.
$\boxed{\displaystyle\sum_{n\geq 1} a_n < \infty \iff \int_0^\infty \lambda(t)dt < \infty}$
ببین که اگر $\lim a_n = 0$ باشه، خوبه که یکپارچگی را فقط در (0,1) بررسی کنی
تست کوشی
که با حد بالایی $\lambda_n=\sqrt[n]{a_n}$ سروکار داره ، اما زمانی که حد بالایی 1 باشد به نتیجه نمی رسه
آزمون دالامبر
که با حد بالا یا پایین $\lambda_n=\frac{a_{n+1}}{a_n}$ سروکار داره
، اما زمانی که $ limit ≥1 $ باشد به نتیجه نمی رسه $ limit ≤1$
آزمون برتراند
که با $\lambda_n= (\ln n)\Big[n\Big(\frac{x_n}{x_{n+1}}-1\Big)-1\Big]$ سروکار دارد.
، اما هنوز وقتی $\lim\lambda_n=1$ به نتیجه نمیرسه
مثال من میگم $\sum\limits_{n = 1}^\infty {\large\frac{{{e^{\frac{1}{n}}}}}{{{n^2}}}\normalsize}$همگراست ببین ${e^{\large\frac{1}{n}\normalsize}} \le e$ازمون میزارم $\large {\sum\limits_{n = 1}^\infty {\frac{{{e^{\large\frac{1}{n}\normalsize}}}}{{{n^2}}}} }
\le {\sum\limits_{n = 1}^\infty {\frac{e}{{{n^2}}}} }
= {e\sum\limits_{n = 1}^\infty {\frac{1}{{{n^2}}}} .}$خوب چون $\sum\limits_{n = 1}^\infty {\large\frac{1}{{{n^2}}}\normalsize}$همگراست پس سری اصلی همگراست
همیشه دالامبر هم جواب نمیده ها
دقت کن $\sum_{n=1}^{\infty}Ln(\frac{ne^{1/n}}{n+1}) = 0.577216$و $\sum_{n=1}^{\infty}Ln(\frac{ne^{1/n}}{n+1})converges$
اینم مرغ پاک کرده میدونه $L = \mathop {\lim }\limits_{n \to \infty } \left| {\frac{{{a_{n + 1}}}}{{{a_n}}}} \right|$مثال من $L < 1$
بازم میگم بیایید نگاهی به $\sum_{k = 1}^{\infty} a_n$ بیندازیم
(جایی که $a_n \in \mathbb{R}$ یا $a_n \in \mathbb{C}$ برای هر n∈N دارم $\limsup_{n \rightarrow \infty} $
یعنی سری $\sum_{k = 1}^{\infty} a_n$ کاملاً همگرا میشه
$\lim_{n \rightarrow \infty} |\frac{a_{n+1}}{a_n}| > 1$یعنی سری $\sum_{k = 1}^{\infty} a_n$ واگرا میشه.
از هر آزمونی برای تعیین همگرایی سری $\sum_{n=1}^\infty \frac{(-1)^ne^{\frac{1}{n}}}{n^3}$استفاده کنید
آزمون مقایسه از طریق: $e^{1/n}\leq 3$ انجام میشه
بنابراین $\left|(-1)^{n}\dfrac{e^{1/n}}{n^{3}}\right|\leq\dfrac{3}{n^{3}}$
یک تست مقایسه محدود انجام دهید. اگر$b_n = \frac{1}{n^3}$ را انتخاب کنین
بعدش $\lim_{n \to \infty} \frac{a_n}{b_n} = \lim_{n \to \infty} e^{\frac{1}{n}} = 1 \gt0$
این بدان معنی است که هر دو $\sum a_n$
و $\sum b_n$ بر اساس همگرایی/واگرایی $\sum b_n$ یا همگرا یا واگرا میشه
.همانطور که من گفتم $\sum_{n=1}^\infty\frac{1}{n^3}$ یک سری p همگرا هستش و بنابراین با آزمایش مقایسه حدی سری اصلی من کاملاً همگراهست.
.ببین یک مثال از کتابم $\sum_{n= 1}^{\infty} \frac{(-1)^n\ln(n)}{n(n+1)} = 0.063254$
$\begin{align}\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n(n+1)}&=\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}n-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\\&=\frac d{dx}\sum_{n=1}^\infty\frac{(-1)^nn^x}n\bigg|_{x=0}-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\\&=\eta'(1)-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\\&=\gamma\ln(2)-\frac12[\ln(2)]^2-\sum_{n=1}^\infty\frac{(-1)^n\ln(n)}{n+1}\end{align}$


