تنشن یک نیروی درونی در جسم مانند طناب است که در برابر هر گونه تلاش برای جدا کردن طناب مقاومت می کند. به سادگی، استرس به دلیل فعل و انفعالات بین مولکولی ایجاد می شود و اگر وجود نداشت، طناب ها در لحظه ای که آنها را می کشید از هم می پاشید.
حال باید بین نیروهای درونی و بیرونی یک جسم تمایز قائل شد. نیروهای خارجی نیروهایی هستند که در اثر اجسام دیگر مانند اصطکاک و جاذبه بر جسم وارد می شوند. وقتی به جسم به عنوان یک کل نگاه می کنید، به راحتی می توانید تأثیر نیرو را بر جسم مشاهده کنید. نیروهای خارجی به بخش عمده جسم اجازه شتاب می دهند، مشروط بر اینکه هیچ نیروی خارجی دیگری آنها را خنثی نکند (تعادل). به عنوان مثال: جسمی که گرانش زمین بر آن اثر می گذارد:
نیروهای درونی جسم متفاوت است. نیروهای درونی در داخل جسم وجود دارند و اثرات نیروهای درونی نمی توانند مستقیماً با هیچ چیز خارجی جسم ارتباط برقرار کنند. به عبارت دیگر، نیروهای درونی نیروهایی هستند که بخشی از یک جسم به قسمت دیگری از همان جسم وارد می کند . از این رو دیدن جهت چنین نیروهایی چندان واضح نیست. نیروهای داخلی منجر به شتاب حجیم نمی شوند، بلکه باعث تغییر شکل جسم می شوند (مثلاً تنشن فنر یا خم شدن یک خط کش).
خوب، شما نمی توانید چیزی آشکار در بیرون ببینید، اما این به این دلیل نیست که نیروی داخلی وجود ندارد. به این دلیل که اگر بخواهید تمام نیروهای درونی موجود در یک جسم را بگیرید، مجموع آنها صفر می شود. این نتیجه قانون سوم نیوتن است. در عوض، یک راه بهتر برای تجسم نیروهای داخلی در جسم این است که یک برش خیالی در جسم ایجاد کنید و ببینید نیروها بر روی صورت بریده شده چگونه عمل می کنند. این بهتر در نمودار زیر نشان داده شده است، جایی که یک طناب از هم جدا می شود:
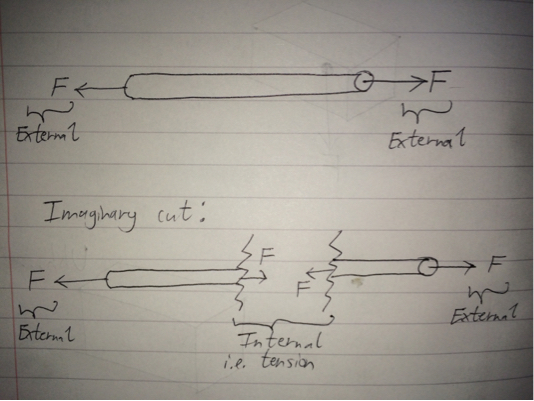
با در نظر گرفتن یک برش خیالی، به دو نیمه نگاه میکنید و تعادل را اعمال میکنید (اگر کل طناب از تعادل تبعیت میکند، هر زیرطول دلخواه طناب نیز باید رعایت شود). با انجام این کار، متوجه می شوید که برای ارضای تعادل، یک نیمه باید به دیگری نیرو وارد کند و برعکس قانون 3 نیوتن. این نیروهای خاص داخلی هستند، زیرا نیروهایی هستند که توسط بخشی از طناب که بر روی قسمت دیگری از همان طناب عمل می کند، ایجاد می شوند. این نیروهای داخلی در فصل مشترک برش فرضی عمل می کنند و در این مورد به عنوان تنشن شناخته می شوند. به بیان دقیق تر، این تنشن در محل روی طناب است که برش خیالی در آن انجام می شود. توجه داشته باشید که اگر به نیمی از طناب نگاه کنید، می توانید تنشن دایرکشن را تعیین کنید، اما از آنجایی که تنشنز به صورت جفتی رخ می دهند، هیچ جهت مشخصی برای تنشن در آن نقطه طناب برای کل طناب وجود ندارد.
با نگاهی به مثال شما، اجازه دهید چند برش برای مشاهده نیروهای تنشن در طناب ایجاد کنیم:
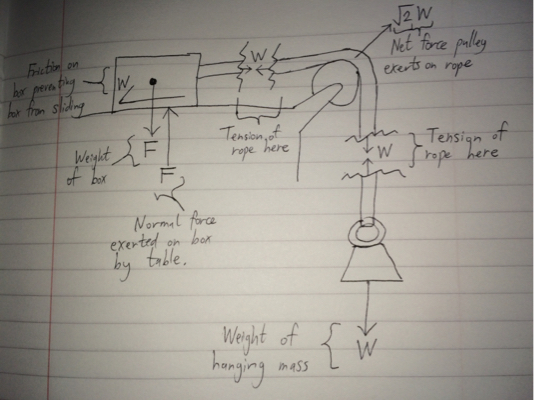
به طور خلاصه، نیروهای داخلی مانند تنشن در یک نقطه خاص در یک طناب واقعاً جهت برش مشخصی ندارند، زیرا به صورت جفت اتفاق میافتند.تنشن روی یک رشته بین دو جسم مشابه نیروی بین دو جسم است که به طور کشسانی برخورد می کنند. نیرویی که از یک سر ریسمان وارد می شود مخالف و برابر با نیروی وارد شده از طرف دیگر ریسمان است. هر دو نیرو باید موازی با رشته و به سمت مرکز آن باشند.
با این حال، تنشن رشته را با یک نیرو اشتباه نگیرید. حتی اگر اندازه نیرویی که در دو سر رشته وارد میشود، باشد و در امتداد طول رشته باشد، تنشن جهتی ندارد. شما نمی توانید بگویید تنش به سمت چپ است و منطقی نیست.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering