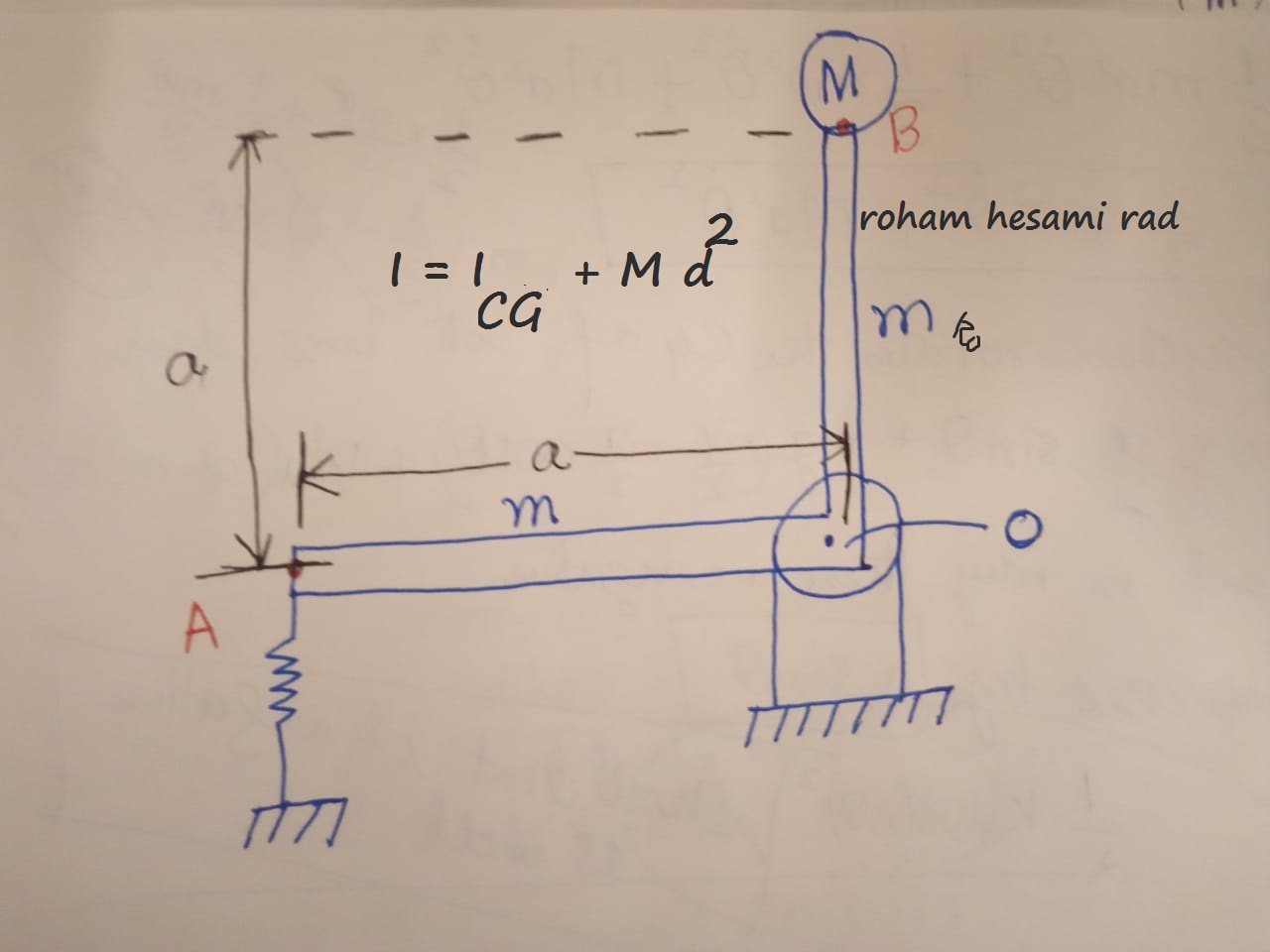
، نه CG مربوطه آنها. برای محاسبه این دو روش موجود است.
استفاده از گشتاورهای جرمی اینرسی میله های صلب OA و OB در مورد لولا O
، که با استفاده از قضیه محور موازی به دست می آید. ما از این روش برای استخراج معادلات حرکت با استفاده از معادله لاگرانژ استفاده خواهیم کرد.
$I_{O} = I_{CG} + M d^{2}$
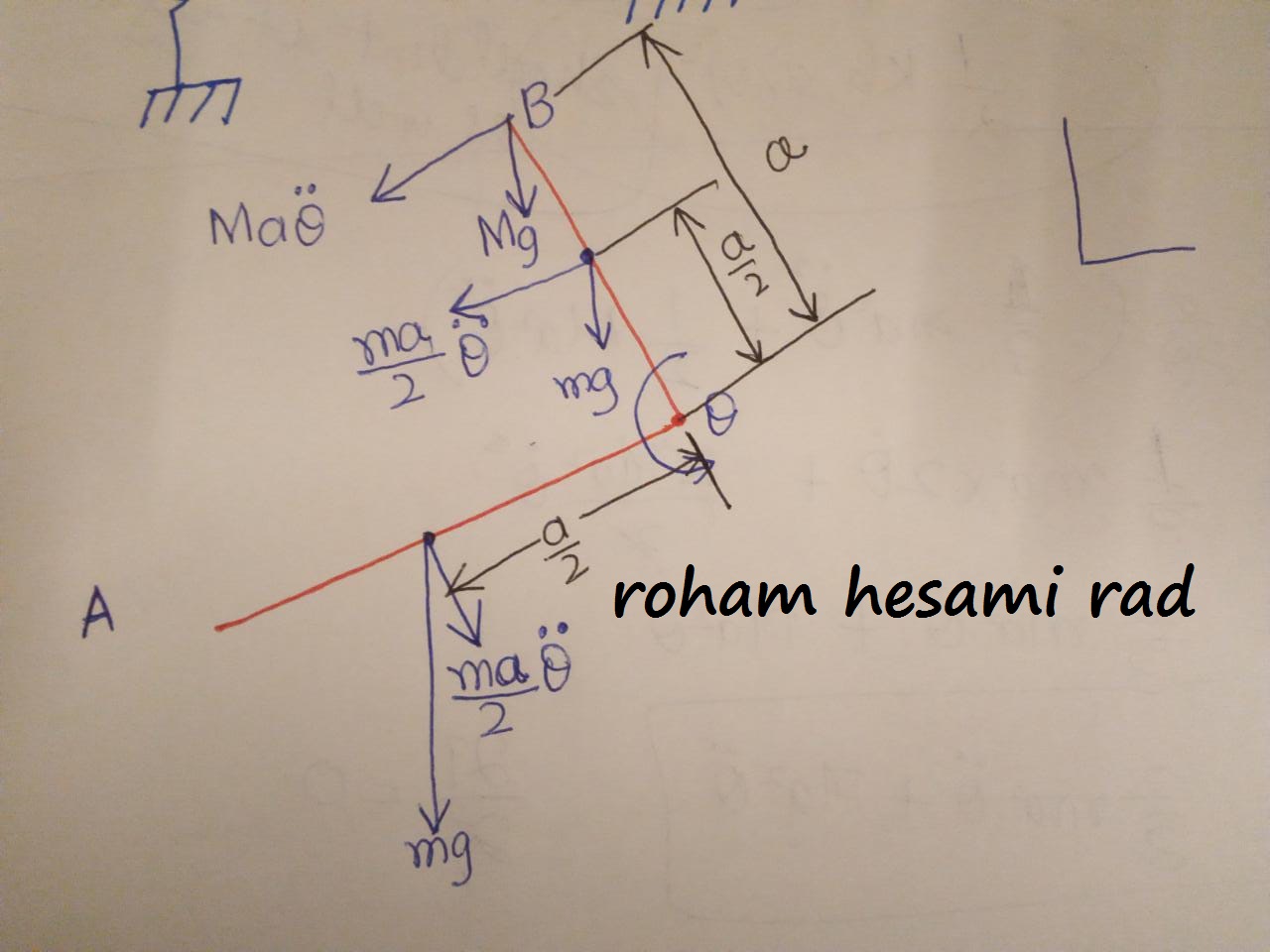
استفاده از گشتاورهای جرمی اینرسی میله های صلب OA و OB در مورد CGهای مربوطه خود و لحظه های نیروهای عادی و مماسی ایجاد شده در اثر چرخش را در نظر می گیرند. از آنجایی که خط عمل نیروی نرمال (نیروی مرکزگرا AKA داده شده توسط$\mathrm{m r \dot{\theta}^{2}}$
) از محور چرخش می گذرد، گشتاور آن طبق تعریف صفر است و فقط ممان نیروی مماسی $\mathrm{m r \ddot{\theta}}$
) باید مشخص شود. ما از این روش برای استخراج معادله حرکت با استفاده از قانون دوم نیوتن استفاده خواهیم کرد.
برای بدست آوردن معادله حرکت، فقط از تعادل لحظه ای در مورد نقطه O استفاده می کنیم
. از آنجایی که قبلاً دیدیم که گشتاورهای ناشی از نیروهای عادی صفر است و لحظه واکنش لولا نیز صفر است، آنها را در نمودار جسم آزاد نشان نمیدهیم.
ممان ناشی از $\mathrm{\dfrac{m a \ddot{\theta}}{2}}$
اقدام بر روی CG OA: $\mathrm{\dfrac{m a \ddot{\theta}}{2}
\times \dfrac{a}{2} = \dfrac{m a^{2} \ddot{\theta}}{4}}$
ممان ناشی از $\mathrm{\dfrac{m a \ddot{\theta}}{2}}$
اقدام بر روی CG $\mathrm{\overline{OB}}$
$\mathrm{\dfrac{m a \ddot{\theta}}{2} \times \dfrac{a}{2} = \dfrac{m a^{2} \ddot{\theta}}{4}}$
ممان ناشی از $\mathrm{m a \ddot{\theta}}$
عمل بر روی جرم نقطه ای M
$\mathrm{M a \ddot{\theta}\times a = M a^{2} \ddot{\theta}}$¨
ممان به دلیل وزن$\mathrm{mg}$
از $\mathrm{\overline{OA}}$
$\mathrm{\dfrac{a}{2} \cos \theta \times m g}$
ممان به دلیل وزن $\mathrm{mg}$
از$mathrm{\overline{OB}}$
$\mathrm{\dfrac{a}{2} \sin \theta \times m g}$
ممان ناشی از وزن Mg
جرم نقطه ای M
$\mathrm{a \sin \theta \times M g}$
ممان ناشی از نیروی فنر Kasinθ
$\mathrm{-K a \theta \times a}$
هنگامی که ممان تمام نیروهای اعمال شده و اینرسی تعیین شد، گام نهایی اعمال قانون دوم نیوتن برای چرخش حول لولا O است.
.$\left( J_{CG} \right)_{OA} \ddot{\theta} + \left( J_{CG} \right)_{OB} \ddot{\theta} + \left( J_{CG} \right)_{M} \ddot{\theta} + \dfrac{m a^{2} \ddot{\theta}}{4} + \dfrac{m a^{2} \ddot{\theta}}{4} + M a^{2} \ddot{\theta} = \dfrac{a}{2} \cos \theta \times m g + \dfrac{a}{2} \sin \theta \times m g + a \sin \theta \times M g - K a \theta \times a$
جایگزین $\mathrm{\left( J_{CG} \right)_{OA} = \left( J_{CG} \right)_{OB} = \dfrac{ma^2}{12}}$ و $\mathrm{\left( J_{CG} \right)_{M} = 0}$
و ساده سازی می دهد
$\left(\dfrac{2}{3} m a^{2} + M a^{2} \right) \ddot{\theta} + K a^{2} \theta = \dfrac{m g a}{2} \left( \sin \theta + \cos \theta \right) + M g a \sin \theta$
در ادامه همین معادله حرکت را با استفاده از معادله لاگرانژ به دست خواهیم آورد.
همانطور که قبلاً بحث شد، در این بخش، از گشتاورهای جرمی اینرسی در مورد لولا O استفاده خواهیم کرد
. با استفاده از قضیه محور موازی، گشتاورهای جرمی اینرسی میلههای صلب OA¯ و OB¯ در مورد لولا O
برابر هستند و با$\mathrm{\dfrac{m a^{2}}{12} + \dfrac{m a^2}{4} = \dfrac{m a^2}{3}}$داده می شوند
. گشتاور جرمی اینرسی جرم نقطه ای M در مورد لولا O توسط $\mathrm{M a^{2}}$ داده شده است
.$T = \dfrac{1}{3} m a^{2} \dot{\theta}^{2} + \dfrac{1}{2} M a^{2} \dot{\theta}^{2}$
خط مرکزی نوار OA منبع انرژی پتانسیل صفر را مشخص می کند. در نتیجه چرخش مثبت سیستم، هر سه جزء در میدان گرانش سقوط می کنند. بنابراین، انرژی بالقوه آنها منفی خواهد بود.
$U_{g} = -m g \dfrac{a \sin \theta}{2} - m g \dfrac{a \left( 1 - \cos \theta \right)}{2} - M g a \left( 1 - \cos \theta \right)$
انرژی پتانسیل الاستیک سیستم به وسیله
$U = -m g \dfrac{a \sin \theta}{2} - m g \dfrac{a \left( 1 - \cos \theta \right)}{2} - M g a \left( 1 - \cos \theta \right) + \dfrac{1}{2} K \left( a \theta \right)^2$
ارزیابی اصطلاحات در معادله لاگرانژ:
$\dfrac{d}{d t} \left( \dfrac{\partial T}{\partial \dot{q}_{1}} \right) = \dfrac{2}{3} m a^{2} \ddot{\theta} + M a^2 \ddot{\theta} \\\\$
$\dfrac{\partial T}{\partial q_{1}} = 0 \\$
$\dfrac{\partial U}{\partial q_{1}} = -\dfrac{m g a}{2} \cos \theta - \dfrac{m g a}{2} \sin \theta - M g a \sin \theta + K a^{2} \theta$
با q1=θ. جایگزینی مقادیر به معادله لاگرانژ می دهد
$\dfrac{2}{3} m a^{2} \ddot{\theta} + M a^2 \ddot{\theta} - \dfrac{m g a}{2} \cos \theta - \dfrac{m g a}{2} \sin \theta - M g a \sin \theta + K a^{2} \theta = 0$
تنظیم مجدد معادله بالا همان معادله حرکتی را می دهد که قبلاً بدست آمده بود.
$\left( \dfrac{2}{3} m a^{2} + M a^2 \right) \ddot{\theta} + K a^{2} \theta = \dfrac{m g a}{2} \left( \cos \theta + \sin \theta \right) + M g a \sin \theta$
با فرض چرخش های زیاد، آیا این مشتقات صحیح هستند؟
آیا معادله حرکت بیشتر شبیه این نیست:
$\begin{align}
\left( \frac{2\,ma^2}{3} + Ma^2\right)\,\, \frac{d^2 \theta}{dt^2}\, =\, - \, \frac{amg}{2} \, \cos(\theta) \, + \, \left(\frac{amg}{2} + aMg \right)\, \sin(\theta) \, - \, aK\left(2a\, \sin\Big(\frac{\theta}{2}\Big) \, - \, l_0\right) \cos\Big(\frac{\theta}{2}\Big)
\end{align}$ساده ترین راه استفاده از چارچوب مکانیک لاگرانژی است.
اجازه دهید با یک تصویر از نحوه عملکرد سیستم شروع کنم، به گفته منمن فرض کردم که OA=OB=OC=a
و همچنین $\angle \, AOB = 90^{\circ}$ و اینکه انتهای زیرین فنر در نقطه C به زمین متصل است
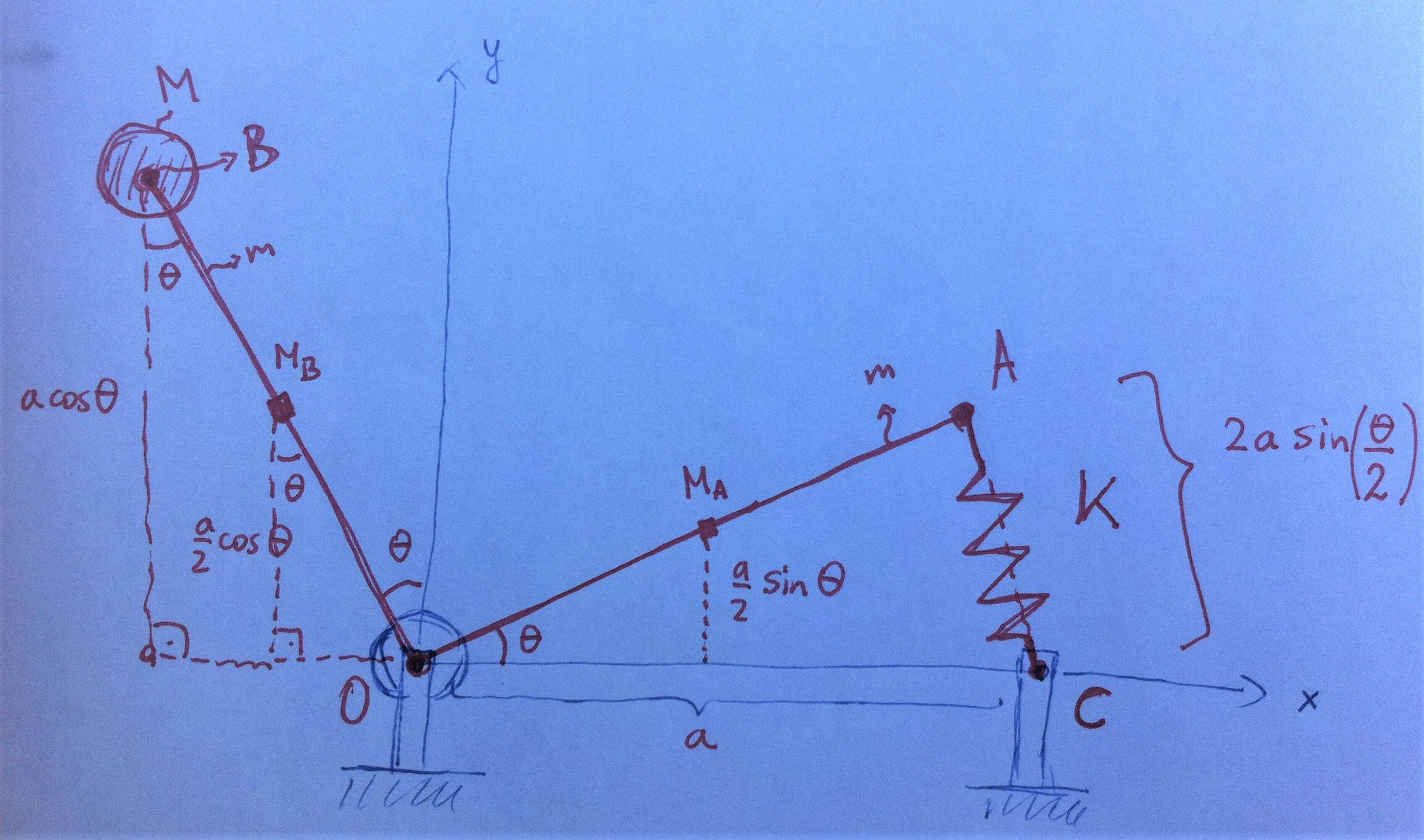
روی تصویر و انتهای بالایی آن به قاب OAB متصل شده است
در نقطه A، از آنجایی که شما موقعیت دقیق فنر را به وضوح مشخص نکرده اید. از آنجایی که OA=OC
در هر پیکربندی، مثلث AOC همیشه متساوی الساقین است و می توانیم فاصله را محاسبه کنیم $|AC| = 2a \, \sin\left(\frac{\theta}{2}\right)$
.جسم متحرک OAB با نقطه جرم اضافی B با جرم M باید دارای گشتاور اینرسی مجموع گشتاورهای اینرسی سه جزء OA,OB باشد
و b نسبت به نقطه ثابت چرخش O. با فرض، جرم های های OA,OB
و b m، m هستند و m به ترتیب. بنابراین، باید گشتاورهای اینرسی دو میله صلب OA را با هم جمع کنیم
و OB و یک نقطه جرمی B نسبت به O
. از این رو$I = I_{OAB,B} = \frac{ma^2}{3} + \frac{ma^2}{3} + Ma^2 = \frac{2\,ma^2}{3} + Ma^2$
در نتیجه انرژی جنبشی این سیستم است
$T = \frac{1}{2}\left(\frac{2\,ma^2}{3} + Ma^2 \right)\, \left(\frac{d\theta}{dt}\right)^2$تمام نیروهایی که بر روی سیستم وارد می شوند نیروهای بالقوه هستند:
نیروی جاذبه بر روی میله OA اثر می کند به مرکز جرم آن، نقطه میانی MA اعمال می شود
. انرژی پتانسیل آن است$U_A = mg\, y_{M_A} = \frac{amg}{2} \, \sin(\theta)$
نیروی جاذبه بر روی میله OB به مرکز جرم آن، نقطه میانی MB اعمال می شود
. انرژی پتانسیل آن است$U_B = mg\, y_{M_B} = \frac{amg}{2} \, \cos(\theta)$
نیروی گرانش بر روی نقطه جرمی B. انرژی پتانسیل آن است
$U_M = Mg\, y_{B} = aMg \, \cos(\theta)$نیروی الاستیک، که احتمالاً از قانون هوک پیروی می کند، بنابراین نیرویی با پتانسیل درجه دوم است:
$U_S = \frac{K}{2} \Big(|AC| - l_0 \Big)^2 = \frac{K}{2} \left(2a \, \sin\left(\frac{\theta}{2} \right)- l_0\right)^2$جایی که $l_0$
طول فنر در حالت تعادل است.
در نتیجه، لاگرانژی سیستم است
$\begin{align}
L \, =& \, T - U_A - U_B - U_M - U_S \\
=& \, \frac{1}{2}\left(\frac{2\,ma^2}{3} + Ma^2 \right)\, \left(\frac{d\theta}{dt}\right)^2 \, - \, \frac{amg}{2} \, \sin(\theta)\\
& \, - \, \frac{amg}{2} \, \cos(\theta) \, - \, aMg \, \cos(\theta) \, - \,\frac{K}{2} \left(2a \, \sin\left(\frac{\theta}{2} \right)- l_0\right)^2
\end{align}$اگر به طور صریح معادله اویلر-لاگرانژ را محاسبه کنیم
$\frac{d}{dt}\left(\,\frac{\partial L}{\partial \dot{\theta}}\left(\,\theta, \, \frac{d\theta}{dt}\,\right)\,\right) = \frac{\partial L}{\partial {\theta}}\left(\,\theta, \, \frac{d\theta}{dt}\,\right)$به معادله دیفرانسیل می رسیم
$\begin{align}
\left( \frac{2\,ma^2}{3} + Ma^2\right)\,\, \frac{d^2 \theta}{dt^2}\, =& \, - \, \frac{amg}{2} \, \cos(\theta) \, + \, \left(\frac{amg}{2} + aMg \right)\, \sin(\theta)\\
&\, - \, aK\left(2a\, \sin\Big(\frac{\theta}{2}\Big)
\, - \, l_0\right) \cos\Big(\frac{\theta}{2}\Big)
\end{align}$


