.موتور مغناطیسی یا موتور مغناطیسی نوعی ماشین با حرکت دائمیه که برای ایجاد چرخش با استفاده از آهنرباهای دائمی در استاتور و روتور بدون منبع انرژی خارجی طراحی شده. چنین موتوری از نظر تئوری و همچنین عملی قابل ساخت نیست درسته طبق قانون اول اینرسی.هر چیزی می تونه بی نهایت بچرخه، اگر اصطکاک وجود نداشته باشه. چرخاندن یک جسم با سرعت ثابت هیچ انرژی برای نگهداری مصرف نمی کنه.حرکت دائمی به حرکتی گفته میشه که برای همیشه و بدون داشتن هرگونه منبع خارجی انرژی، ادامه میده؛ در عمل چنین چیزی به علت وجود اصطکاک ناممکنه همچنین میتوان اینو حرکت یک ماشین فرضی که پس از فعال شدنش برای همیشه به کار خود ادامه میده، مگر آنکه در معرض یک نیروی خارجی یا فرسایش قرار بگیره توصیف کرد.
نظر و اصول علمی که حرکت دائمی در یک سامانهٔ مجزا منجر به نقض قانون اول ترمودینامیک و/یا قانون دوم ترمودینامیک میشه.
من فیزیکدان نیستمفقط دانشجوی مهندسی هعوافضا با مغناطیس زیاد سر کار ندارم اما ماشینها چرا ، اما قانونهای ترمودینامیک را می دانم و این را با ایده ای که مدتی پیش به ذهنم رسید برای ایجاد ماشین حرکت دائمی مرتبط کردم که طبق قانون اول ترمودینامیک غیرممکنه.
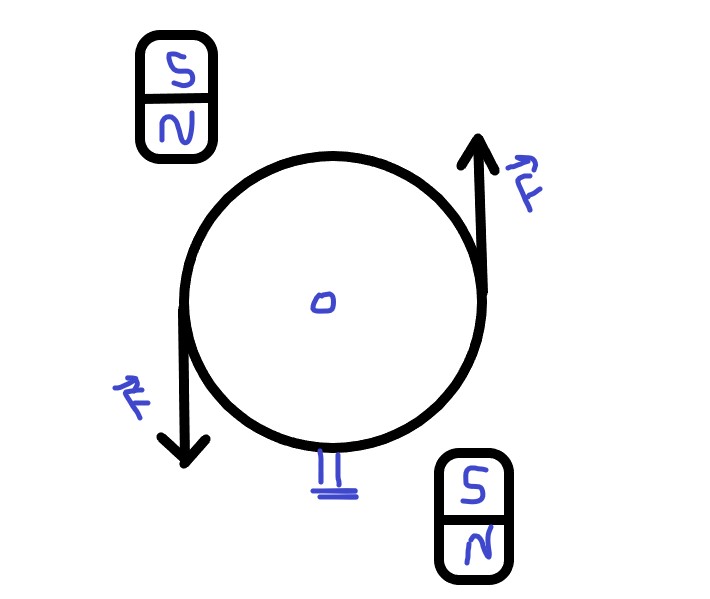
این چرخ از مواد فرومغناطیسی ساخته شده بنابراین نیرویی به چرخ وارد میشه که باعث ایجاد گشتاورمیشه اگر این چرخ را بدون هوا در جای خود قرار دهیم، و اینها آهنرباهای دائمی هستند، بنابراین به طور دائم نیرویی وارد می کنند، و اتم ها در مواد فرومغناطیسی تراز نمی شود زیرا دائمی ها در جهت مخالف هستند پس چگونه این چرخ شتاب را متوقف می کنه؟
من اشتباه می کنم که گشتاور روی چرخ وجود داره. در حالی که میدان مغناطیس دائمی ممکنه کمی روی برخی از بخشهای چرخ بکشه، میانگین کشش کل دقیقاً به صفر میرسه.
بله، برخی از قطعات چرخ می خواهند در جهت عقربه های ساعت حرکت کنند تا به آهنربا نزدیک شوند، اما برخی از قطعات چرخ می خواهند در خلاف جهت عقربه های ساعت حرکت کنند تا نزدیکتر بشن. ما نمیتوانیم فقط بیتها را مستقیماً در مقابل قطب آهنربا در نظر بگیریم. کل میدان مغناطیسی باید در نظر گرفته بشن. هنگامی که جمع میشه (با فرض همگن بودن چرخ)، گشتاور صفره .
کمکی نخواهد نمیکنه چرخ می چرخد تا حالت حداقل انرژی پتانسیل را اشغال کند (درست مانند سنگی که در سراشیبی می غلته). اگر آن حالت منحصربهفرد باشه به آنجا میغلته و دور نمیشود (مثل صخرهای در کف دره). اگر حالت منحصر به فرد نباشه میدان نیرو گشتاور ایجاد نمی کنه دقیقا مثل چرخ فلک گرانش نمی تونه باعث چرخش چرخ و فلک شود). –
شکل مهم نیست آیا می دانید (حداقل در اصل) چگونه انرژی پتانسیل یک جسم را در یک میدان محاسبه کنید؟ تصور کنید چرخاندن چرخ چگونه این انرژی را کمی تغییر میده. اگر انرژی پتانسیل را آزاد کنه، در آن جهت حرکت می کنه. شما باید میدان مغناطیسی را پیدا کنین که در آن با چرخش چرخ انرژی کمتر بشه. برای یک چرخ همگن، این اتفاق نمی افته. برای یک چرخ نامتقارن، حداقل حالت انرژی وجود دارد که نمی توانید از آن دور شوید. –
که نقص استدلالم را روشن می کنه، .
از همه، جهت نیروهای موجود در تصوییر من که زوج را تشکیل می دهند در جهت صحیح نیستند. که فلشهای سیاه را در نمودار خود معکوس کنید. با این حال من چیزی را از دست دادم و برایمن 0 می آید
گشتاور خالص
در اینجا، اگر با دقت ببینیم، دو جفت گشتاور (با رنگ بنفش مشخص شده) را می بینیم که متقابلاً یکدیگر را خنثی می کنند.
از این رو، این ایده ممکن است خیلی خوب کار نکند.
برای تجزیه و تحلیل با جزئیات بیشتر، من فکر می کنم ما باید فعل و انفعالات ناشی از آهنربا را نیز در نظر بگیریم، اما این موضوع را پیچیده تر می کند و علاوه بر این در اینجا کاربرد زیادی ندارد.
دلیلی که من در مورد اینکه چرا اصولاً ساختن یکی از این موارد غیرممکن است به خاطر می آورم بر این واقعیت استوار است که واگرایی میدان مغناطیسی صفر است. این بدان معناست که نمیتوان مجموعهای از آهنرباهای دائمی را به گونهای ترتیب داد که اجازه دهیم یک آهنربا به دیگری "دزدیده شود" و سپس ناگهان دفع یا جذب آن شود و سپس "رها شود" تا جفت آهنربای بعدی آهنرباهای موجود در آرایه می توانند این روند را تکرار کنند و دسته ای از "انرژی رایگان" را برای شما بچرخانند.
من یک منبع می گویم که اگر بدون اصطکاک باشد ، کار می کند و ما سعی نمی کنیم از آن انرژی بگیریم (اینجا) ، بنابراین به تعبیری خاص ، بسیار نزدیک است (ممکن است آنها یک تجزیه و تحلیل کامل ارائه ندهند .)فرض سقوط توپ از طریق سوراخ مشکلی ندارد. حتی اگر نیروی مغناطیسی زیاد باشد ، فقط باید از مولفه گرانش در امتداد سطح شیب دار بزرگتر باشد. این جز mg mgcosθ است. هنگامی که توپ به سوراخ می رود ، جاذبه توپ احساس می شود به میلی گرم ، بنابراین ممکنه توپ ای که در ابتدا بالا می رفت اکنون پایین بره
با این حال ، توجه کنید که وقتی توپ به سمت پایین حرکت می کند ، نیروی جاذبه دوباره شروع به کاهش می کنه (در حال افقی شدن است همچنین با دور شدن توپ از آهنربا ، نیروی مغناطیسی نیز کاهش می یابد. اگر یک نمودار در مورد هر دو نیرو ایجاد کنید ، می بینید که همیشه وجود دارد نقطه ای در مسیر توپ زمانی که هر دو نیرو دارای اندازه یکسانی هستند اما علامت مخالف دارند. این موقعیت تعادل توپ خواهد بود ، در صورتی که اگر تمام انرژی جنبشی اولیه آن را استخراج کنید ، در حالت استراحت خواهد ماند. بنابراین بعد از همه.
فیزیک نیوتونی قطعاً از وجود هر حرکت دائمی "واقعی" جلوگیری می کند. تحت شرایط خاص ، می توانیم با اعمال منطقی اصول به حرکتی تقریباً دائمی دست یابیم و سپس سوالاتی مانند "اگرچه هیچ کاری را نمی توان از سیستم حذف کرد ، اما آیا طول عمر نیروی مغناطیسی در یک آهنربا کافی است که برای چندین سال کارکرد قابل قبول است" پاسخ؟"
جاذبه نیروی که باید در این آزمایش غلبه کرد ، اصطکاک فقط قسمت کوچکی داره، اما ما همچنین نمی توانیم جریان القایی در حرکت توپ را نادیده بگیریم ، که در نهایت به نیروی اصلی تخریب دوام حرکت تبدیل می شود. در اینجا ، اگر آهنربا به اندازه کافی قدرت داشت تا بر اینرسی و نیروی گرانش وزن بر روی یک شیب غلبه کند ، انرژی کافی برای اتصال به آهنربا در بالا خواهد داشت. حتی بدون اصطکاک ، و بگذارید بگوییم که ما توپ را از بالا شروع کردیم تا یک نیروی جنبشی اولیه به آن بدهیم ، وقتی به سوراخ دوم رسید ، آهنربا نه تنها باید بر نیروی جاذبه غلبه کند ، بلکه حرکت کلی دور از آهنربا در بالا ، همانطور که از سوراخ 2 عبور می کند ، بیشتر شبیه اسکی بازانی می شود که پرش اسکی انجام می دهند و از ماشین دور می شوند. بنابراین آهنربا نیز باید این حرکت را انجام دهد و جهت توپها را معکوس کند زیرا اکنون نیز با سرعتی برابر با انرژی جنبشی حاصل از انداختن توپ منهای اصطکاک دور می شود.
یک سطح شیب دار اضافی در پایین بر این مسئله غلبه می کند ، که با تبدیل حرکت خطی به حرکت زاویه ای که جهت توپ را معکوس می کند و آن حرکت جنبشی را حفظ می کند تا توپ را به سمت نیمه رمپ حرکت دهد. حتی در این صورت ، این برای غلبه بر جاذبه ، اصطکاک و نیروی مقابله با یک جریان القایی کافی نیست تا بتواند توپ را تا انتها بکشد ، در حالی که به اندازه کافی ضعیف است تا توپ را از سوراخ رها کند. من معتقدم ، اما آزمایش یا اثبات نکرده ام ، که شاید کاهش جاذبه این دستگاه را مانند ماه امکان پذیر کند. همچنین به نظر می رسد ، از آنجا که توپ از فلز ساخته شده است که به آهن ربا جذب می شود ، نیروهای موجود در توپ می توانند یک میدان شمارنده جریان القایی را تنظیم کنند ، به دلیل ماده ای که توپ ساخته شده و در میدان است. یک اثر لنز معکوس وجود دارد که همچنین می تواند نیرویی را که مغناطیس باید از آن عبور کند ، کمک کند. این امر به یک تعادل فوق العاده زیبا بین یک نیروی کاملاً جذاب و نیروهای مخالف نیاز دارد. دستگاه بسیار امیدوار کننده به نظر می رسد. اما ، در یک سطح بسیار ظریف دارای نیروهای متقابل از جاذبه ، اصطکاک و یک اثر معکوس لنز است که با انرژی جنبشی ساخته شده در حرکت توپها مقابله می کند که باعث می شود عمل به سرعت ادامه یابد.
، از طریق فشار دادن قدرت آهنربا الکتریکی پنهان شده در پایه که آهنربا دائمی را پنهان کرده است ، بر این اثر غلبه می کند. با خاموش کردن آهنربای الکتریکی در لحظه مناسب یا به صورت دستی یا با حس القایی ، توپ افت می کند. موافقم که بسیار نزدیک به امکان است. اما ، این فقط امکان پذیر نیست من تصور می کنم که ممکن است بتوانم نیروی جاذبه را تغییر دهم تا عملکرد دستگاه تحت نیروی جاذبه مناسب کافی باشد ، اما واقعاً این نگرانی را دارم که جریان های گردابی در توپی فلزی نیروی نهایی را ایجاد کنند که با هرگونه احتمال کار کردن آن مقابله کند.
به عنوان یک مسئله میدان مغناطیسی ، به دلیل قوانین ماکسول و قانون لنز ، مسئله از نظر ریاضی بسیار پیچیده تره ، من تمایل دارم که اثر توپ را روی میدان مغناطیسی نادیده بگیرم زیرا این امر باعث حرکت و تغییر چگالی شار می شود جریانی را القا می کند که در حرکت و تراکم شار در مخالفت با حرکت تأثیر می گذارد
چه چیزی مانع از کارکرد این متحرک مغناطیسی perpetuum ممیشه
من درزمان درس فیزیک 2 ترم دوم این وسیله را تصور می کردم که ممکن است به نظر برسد که به طور نامحدود می چرخه. دو تا سوال دارم
آیا این دستگاه حرکت دائمی از قبل شناخته شده است؟ اگر هست لطفا چند مرجع بفرمایید؟
مکانیسم دقیقی که باعث توقف آن می شود چیست؟ منظور من از این توضیح یک توضیح است، نه صرفاً "زیرا قانون بقای انرژی را زیر پا می گذارد". البتهبقای در انرژی درست است و این دستگاه نمی تواند به طور نامحدود کار کند. اما برای هر متحرک دائمی شناخته شده (فرض شده)، توضیحی وجود داشت که معمولاً مبتنی بر نشان دادن این است که نیروی ایجاد کننده حرکت توسط نیروی دیگری متعادل است. به عنوان مثال، استوین قوانین صفحه شیبدار را از دستگاه حرکت دائمی به دست آورد
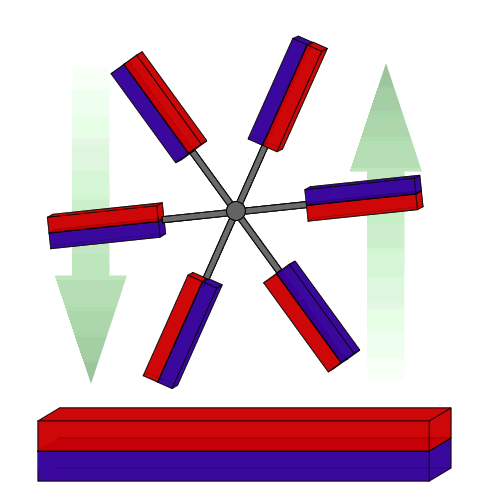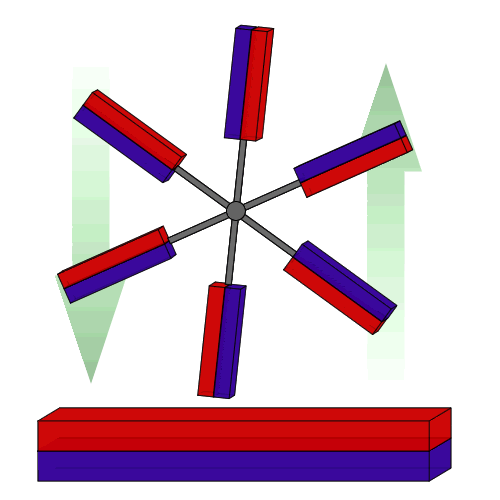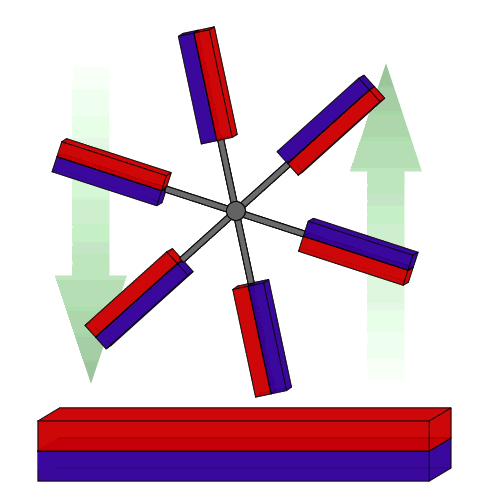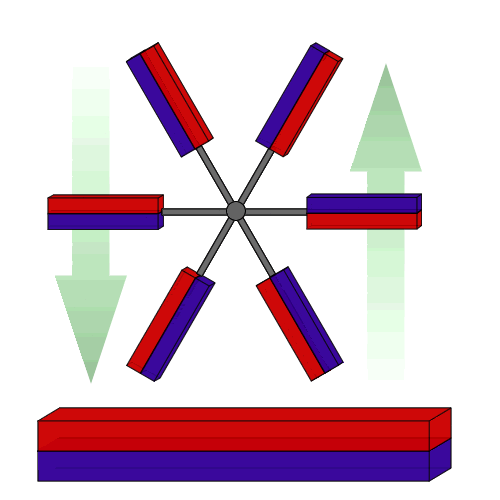
مغناطیسی پرپتووم متحرکمن می خواهم برخی از مشاهدات را انجام دهم.
من سعی نمی کنم کسی را متقاعد کنم که برای همیشه حرکت خواهد کرد زیرا به شکستن بقای در انرژی اعتقادی ندارم.
اما من توضیح کافی برای اشاره به بقای در انرژی نمی دانم. من علاقه مند به توضیحی هستم که دقیقاً چگونه نیروهای مغناطیسی که باعث چرخش آن می شوند، متعادلند
اگر نیروها متعادل باشند، تنها در این صورت اصطکاک باعث کاهش سرعت و توقف آن می شود. فکر نمیکنم فقط با رجوع به اصطکاک که اصولاً میتوان آن را به اندازهای که لازم است کوچک کرد، توضیح داد. باید توازن نیروهاوجود داشته باشه
چرا وقت صرف کردن برای درک یا توضیح چیزی که مسلماً نمی تواند کار کند؟ خوب، حتی اگر ماشینهای حرکت دائمی واقعاً نمیتوانند کار کنند، به نظر من ممکن است به عنوان پازل برام جالب باشه کسی که ایده طراحی موتور های بین سیاره ای داره
الکترومغناطیسی میدان مغناطیسی - بقای انرژیشما نیازی به اصطکاک ندارید. نیروهای مغناطیسی به خودی خود در تعادل هستند، بنابراین اگر آهنرباها را در آن پیکربندی قرار دهید، آنها به طور خود به خود شروع به حرکت نخواهند کرد. دلیل آن این است که وقتی آهنرباها عمودی هستند نیروی متناظری روی آهنرباها وجود دارد که با آنهایی که قبلاً کشیده اید مطابقت دارد.
یه مدل ساده بزارم اول از همه، با بالا بردن بازی و اضافه کردن دو آهنربای بزرگ شروع کنید که فقط می تواند آن را بهتر کند:
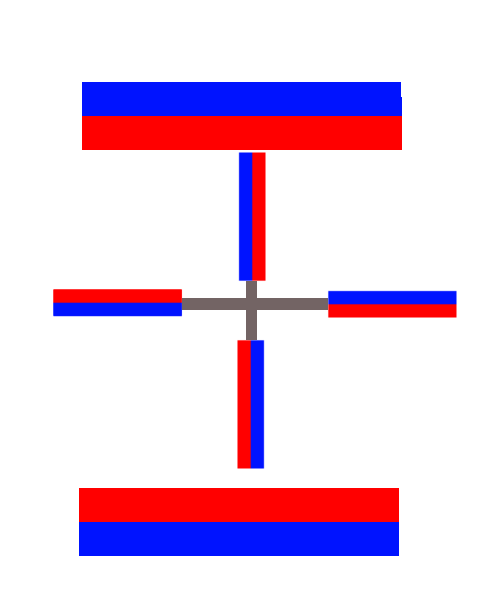
اگر قرمز یک قطب شمال است، پس هر آهنربای دوار، در حالت افقی، دارای یک قطب شمال است که قطب شمال پشتی خود را دفع می کند و یک قطب شمال که قطب جنوب جلویی آن را جذب می کند. با تمرکز روی آهنرباهای بزرگ در حال حاضر، این واقعیت که قطب های شمالی آنها رو به روی یکدیگر قرار دارند نشان می دهد که می توانیم آنها را با یک جفت سیم پیچ ضد هلمهولتز مبادله کنیم. این بدان معنی است که ویژگی مهم میدان آنها ماهیت چهار قطبی آن است و می توانیم میدان مغناطیسی را به صورت تقریبی در نظر بگیریم.
$\mathbf B=\frac{B_0}a\begin{pmatrix}x\\y\\-2z\end{pmatrix},$،
جایی که z محور از یک آهنربای بزرگ به آهنربای دیگر می رود، a
مقداری طول مشخصه است و B0 قدرت میدان مشخصه است.اکنون، برای آهنرباهای کوچک، من فکر می کنم که مدل کردن آنها به عنوان دوقطبی نقطه ای بحث برانگیز نیست. اگر θ زاویه ای است که پره چرخ با x ایجاد می کند محور (با چرخ در x,z
صفحه) پس هر آهنربا یک دوقطبی با ممان است$\mathbf m=m
\begin{pmatrix}-\sin(\theta)\\0\\\cos(\theta)\end{pmatrix}
\text{ at }
\mathbf r=R
\begin{pmatrix}\cos(\theta)\\0\\\sin(\theta)\end{pmatrix}.$⎟.
با این، انرژی پتانسیل هر آهنربای پره ای است
$U=-\mathbf m\cdot\mathbf B=3\frac R a mB_0\sin(\theta)\cos(\theta)=\frac32\frac Ra mB_0\sin(2\theta).$
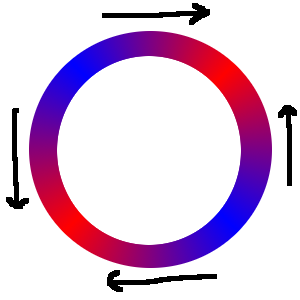
برای اینکه ببینید این چگونه رفتار می کند، در اینجا یک نمودار رنگی از انرژی است که انرژی منفی در قرمز و انرژی مثبت در آبی وجود دارد.
توضیحات تصویر را در اینجا وارد کنید
می توانید ببینید که یک شیب در سمت راست به سمت بالا و در سمت چپ پایین است. با این حال، هنگامی که پره ها عمودی هستند، این شیب ها در جهت عقربه های ساعت مطابقت دارند. یک آهنربا در سمت چپ پایین یا سمت راست بالا قرار می گیرد. یک جفت آهنربا روی آن مورب قرار می گیرد. برای یک چرخ متقارن با سه آهنربا یا بیشتر، انرژی پتانسیل کل در صفر است.
$U=\sum_{k=1}^n\frac32\frac Ra mB_0\sin\left(2\left(\theta_0+\frac{2\pi}{n}k\right)\right)
=\frac3{4}\frac Ra mB_0\text{Im}\left[e^{2i\theta}\sum_{k=1}^n(e^{2\pi i/n})^k\right]
=\frac3{4}\frac Ra mB_0\text{Im}\left[e^{2i\theta+2\pi i/n}\frac{1-(e^{2\pi i/n})^n}{1-e^{2\pi i/n}}\right]
=0$و هیچ نیروی مغناطیسی حاصل وجود ندارد.


