با توجه به جرم m از ارتفاع h سقوط کرد بالاتر از یک مقیاس فنری، آیا روش خوبی برای تقریبی حداکثر قرائت وجود داره؟
اما من فکر میکنم این رویکرد به برخورد بین جرم در حال سقوط و مقیاس الاستیک
مورد پایه شامل قرار دادن m است
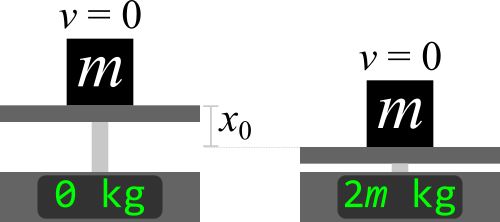
صرف نظر از اصطکاک، بقای انرژی نشان می دهد که حداکثر جابجایی باید $x_0 = \frac{2mg}{k}$ باشد.
. اگر ترازو به درستی کالیبره شده باشد، یعنی m را می خواند
در موقعیت تعادل جدید خود - باید$R_0 = 2m$را نشان دهد
وقتی جرم در پایین ترین نقطه نوسان خود قرار دارد.
استفاده مجدد از بقای انرژی، به جز با m در ارتفاع اولیه h بالاتر از مقیاس:
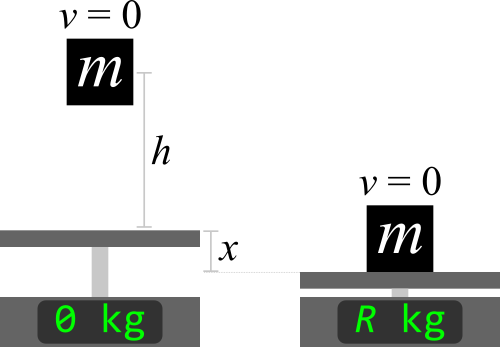
حداکثر جابجایی جدید $x = \frac{mg + \sqrt{mg\left(mg + 2hk\right)}}{k}$است
، که مربوط به حداکثر خواندن است
$R = \frac{1}{2}\left(1 + \sqrt{1 + \frac{2hk}{mg}}\right)R_0 = m\left(1 + \sqrt{1 + \frac{2hk}{mg}}\right)$
این نتیجه در ابتدا قابل قبول به نظر می رسد، اما پس از وصل کردن مقادیر، نتایج وحشیانه هستند. من می دانم که هر مدلی که فقط بر اساس مفاهیم ابتدایی باشد، احتمالاً به فرضیات ضعیف بستگی دارد، اما در تعجبم که آیا رویکرد بهتری وجود دارد که من از آن چشم پوشی کنم.
یک تمرین سرگرمکننده وجود دارد که در آن یک زنجیر عمودی با جرم آویزان میشود و پایین آن بالای یک ترازو را لمس میکند. مشکل این است که وقتی بخش معینی از زنجیره روی ترازو افتاده است، خواندن ترازو را پیدا کنید. یک راه حل از قضیه تکانه- تکانه برای تعیین نیروی اعمال شده توسط مقیاس بر جرم استفاده می کند. به نظر می رسد یک رویکرد مبتنی بر حرکت مانند این به فرضیات کمتری بستگی دارد، اما من تقریباً مطمئن هستم که نمی توان آن را برای یک جرم نقطه سقوط اعمال کرد.
نیروی آنی بین جرم و ترازو وجود دارد، و سپس خواندن ترازو وجود دارد. عوامل مؤثر بر هر دوی اینها به عوامل ناشناخته زیادی بستگی دارد - بنابراین در اینجا فقط چند تفکر کلی وجود دارد.
ابتدا، اگر جرم M را رها کنید از ارتفاع h
روی مقیاس هایی با جرم m، و سپس این دو به عنوان یکی حرکت می کنند، برخورد غیر کشسان و سرعت v در نظر گرفته می شود
درست بعد از برخورد می توان از سرعت$v'$ استخراج کرد
درست قبل از قرار دادن
$v = \sqrt{2gh}\\
v'=\frac{M}{M+m}v$
زمانی که طول می کشد تا جرم شتاب بگیرد با کشش تماس مشخص می شود و به طور کلی مشخص نیست. هر چه زمان کوتاهتر باشد، نیرو بزرگتر است - با میانگین نیروی داده شده توسط
$\int F\;dt = m v'\\
F_av=\frac{mv'}{\Delta t}$
اگر نیروی میانگین زمان را در نظر بگیریم.
با این حال، این نیرو احتمالاً در ترازو شما ثبت نمی شود. من می توانم به سه نوع "اصلی" از مقیاس فکر کنم: ترازوی، مقیاس فنری، و مقیاس "بازگشت به صفر". هیچ یک از آنها نیروی ضربه اولیه را ثبت نمی کنند.
برای تعادل، جرم جسم با مقایسه آن با جرم مرجع در بازوی دیگر تعیین می شود. این چیزی نیست که شما در اینجا به دنبال آن هستید.
برای ترازو فنری، انحراف فنر در زیر بار معیاری برای وزن است: این موردی است که در اینجا قابل تجزیه و تحلیل است.
برای مقیاس «بازگشت به صفر» (نمیتوانم نام مناسب را در نظر بگیرم - نظر کسی؟) مکانیسم مورد استفاده جریانی را در آهنربای الکتریکی ایجاد میکند تا مقیاس را به همان موقعیتی که قبل از اضافه شدن جرم بود بازگرداند. اینها معمولاً پاسخ آهسته دارند اما دقیقترین هستند - از آنجایی که نیرو دقیقاً متناسب با جریان است که مقیاس در همان موقعیت قرار دارد، هیچ تأثیری از پیری بهار، دما و غیره وجود ندارد.
من معتقدم که سؤال شما فقط برای مقیاس بهار قابل پاسخگویی منطقی است. توجه داشته باشید که چنین مقیاسهایی معمولاً "به طور بحرانی میراشونده" هستند (اگرچه این فقط تقریباً درست است زیرا درجه میرایی به جرم بستگی دارد - بنابراین فقط میتوان آن را برای یک جرم به طور بحرانی میرا کرد). اما اجازه دهید در ابتدا آن را کنار بگذاریم.
اگر جسمی با جرم M داشته باشیم سقوط از ارتفاع h روی یک مقیاس فنری با جرم $m<<M$
و ثابت فنر k، انحراف را می توان از پایستگی انرژی محاسبه کرد.
افت کل جرم = h+dانرژی ناشی از افت $E=Mg(h+d)$
این باید برابر با انرژی الاستیک ذخیره شده در حداکثر انحراف باشد:
$\frac12 k d^2 = Mg(h+d)$
می توانیم برای d مرتب کنیم و حل کنیم
$\frac12 k d^2 - Mgd - Mgh = 0\\
d = \frac{Mg ± \sqrt{M^2g^2 + 2 Mghk}}{k}$
این دو ریشه با حداکثر حرکت (هارمونیک ساده) که جرم انجام می دهد مطابقت دارد: برای سؤال شما، ما به ریشه مثبت نیاز داریم. توجه داشته باشید که اگر h=0 باشد
موارد فوق نشان می دهد که حداکثر انحراف مقیاس دو برابر فاصله مورد انتظار خواهد بود.
$d = \frac{2Mg}{k}$
و با کاهش جرم از ارتفاع بیشتر، حداکثر انحراف به سرعت افزایش می یابد. دقیقاً چقدر بیشتر به مقدار k بستگی دارد
- هر چه فنر سفت تر باشد، مقدار k بیشتر است
، و هر چه مقداری که روی ترازو می خوانید بزرگتر باشد زیرا جسم از ارتفاع بیشتری رها می شود. همه اینها با تحلیل خود شما همخوانی دارد.
البته این جایی است که میرایی وارد عمل می شود: یک مقیاس شدید میرا تمام انرژی نوسانی را از بین می برد و به آرامی به مقدار تعادل می رسد بدون اینکه هرگز بیش از حد افزایش یابد. یک مقیاس کم میرا نوسان می کند - در حد میرایی بسیار سبک، مقدار محاسبه شده در بالا را می خواند. اما یک مقیاس بحرانی میرا فقط یک بار بیش از حد خواهد شد، و ما می توانیم مقدار بیش از حد را محاسبه کنیم.
راه حل برای یک نوسان ساز هارمونیک ساده با میرایی بحرانی توسط داده شده است
$x(t) = (A + Bt)\;e^{-\omega_0t}$
A و B را از شرایط اولیه پیدا می کنیم،
$A = x(0)\\
B = \dot{x}(0) + \omega_0 x(0)$
اگر $x(0) = d = \frac{Mg}{k}$ را قرار دهیم
، بیش از حد با سرعت اولیه ای که در بالا محاسبه کردیم به دست می آید. برای مقیاس نور، این سرعت اولیه سرعت v است
جرم پس از سقوط ارتفاع h (من می خواهم ارتفاع اضافی d را نادیده بگیرم که به نظر من کوچک است. وگرنه معادلات خیلی آشفته تر می شوند...) و معادله حرکت می شود
$x(t) = (d + (-v + \omega_0 d)t)e^{-\omega_0 t}$
(علامت منفی وجود دارد زیرا سرعت به سمت موقعیت تعادل است). گرفتن مشتق با توجه به t
ما میتوانیم زمانی را محاسبه کنیم که بیشازحد حداکثر است و آن را دوباره وصل کنیم تا بیش از حد را به دست آوریم:
$-\omega_0 (d + (-v + \omega_0 d)t)e^{-\omega_0 t} + (-v + \omega_0 d)e^{-\omega_0 t}=0\\
-\omega_0 (d + (-v + \omega_0 d)t)+ (-v + \omega_0 d) = 0\\
\omega_0 vt- \omega_0^2 dt + v = 0\\
t = \frac{v}{\omega_0(v-\omega_0 d)}$برای v به اندازه کافی بزرگ $v (v>\omega_0 d)$
، این منجر به افراط (بیش از حد) می شود.
جایگزینیT بازگشت به عبارت x اندازه بیش از حد را نشان می دهد که از آن جرم ثبت شده در ترازویی به دست می آید.
راه حل واضح این است که یک "دشپوت دمپر" به مخلوط اضافه کنید تا معادله حرکت سطح باشد.
$y''(t) + 2 \lambda ~ y'(t) + \omega^2 y(t) = -\alpha w_0.$طبق معمول، در این حالت تعادل به ارتفاع$y_0 = -\alpha w_0 / \omega^2,$ می رسد، که روی ترازو وزن $w_0.$ خوانده می شود.جایگزینی$y_0 = -\alpha w_0 / \omega^2,$
تابع$\eta(t)$می دهد تعریف شده بوسیله ی$\eta''(t) + 2 \lambda ~ \eta'(t) + \omega^2 \eta(t) = 0$
راه حل کلی شامل فرض$\eta(t) = A e^{k t}$ است برای تبدیل این فرمول به فرمول جبری:
$k^2 + 2 \lambda k + \omega^2 = 0,\\
(k + \lambda)^2 = -\left(\omega^2 - \lambda^2\right),\\
k = -\lambda \pm i \sqrt{\omega^2 - \lambda^2}.$
بنابراین تعریف $\bar\omega^2 = \omega^2 - \lambda^2,$
راه حل کلی این خواهد بود:$y(t) = y_0 + e^{-\lambda t}\left(A \cos(\bar \omega t) + B \sin(\bar \omega t)\right)$
شرط مرزی برای A واضح است، $A = -y_0$ به طوری که از $y(0)=0 $شروع می شود. سپس B
با سرعت برخورد جرم با مقیاس فنر تنظیم می شود، $y'(0) = -\lambda A + B \bar \omega = -v_0,$،
بنابراین $B = -(v_0 + \lambda y_0)/\bar\omega.$¯. این نشان می دهد که ما فقط همه چیز را بر $y_0,$ تقسیم می کنیم،
تعریف$u(t) = y(t)/y_0.$
بنابراین راه حل ما به طور کلی این است:$u(t) = 1 - e^{-\lambda t} \left(\cos\bar\omega t + \frac{\lambda + v_0/y_0}{\bar\omega}\sin\bar\omega t\right).$ممکن است بتوانید پس از انداختن جرم بر روی ترازو، این را تجزیه و تحلیل کنید تا پاسخهای معقولی برای سؤالات خود در مورد حداکثر قرائتها بیابید.
هدف دستگاه جاذب انرژی توقف بار متحرک با حداقل بازگشت بار، با حداقل ضربه به بار و حداقل ضربه به تجهیزات اطراف است.
کنترل حرکت اغلب مستلزم توقف یکنواخت بار در حال حرکت است. یک اسنابر لاستیکی، یک فنر فشاری و یک داشپات همگی میتوانند این کار را با جذب انرژی انجام دهند. اسنابر و فنر انرژی را ذخیره میکنند و پس از فشرده شدن آن را آزاد میکنند و در نتیجه برگشت میکنند.داشپات یک سیلندر پر از مایع با دهانهای است که سیال ممکن است به صورت کنترل شده از آن خارج شود. هر نیرویی که بر روی پیستون در سیلندر وارد شود، در ابتدای حرکت با مقاومت بالایی از سیال مواجه میشود، سپس با جمع شدن پیستون بسیار کمتر میشود.
با این حال، هیچ یک از این سه مورد انرژی را به طور یکنواخت هدر نمیدهند. ضربه یک بار متحرک در برابر یک نیروی مقاوم باعث ایجاد نیروهای اوج میشود که به تجهیزات کارخانه یا خود بار منتقل میشود. برای اتلاف یکنواخت انرژی، استفاده از ضربه گیر الزامی است مساحت زیر هر منحنی برابر است، بنابراین انرژی تلف شده برای هر چهار روش جذب انرژی یکسان است.
نمودارهای نیرو در مقابل ضربه را برای بار یکسان نشان میدهد که با همان سرعت حرکت میکند و به یک اسنابر لاستیکی، یک فنر، یک داشبورد و یک ضربه گیر برخورد میکند. انرژی جنبشی قابل جذب در هر مورد یکسان است، اما با سرعتهای متفاوتی تلف میشود. نرخ خطی کاهش سرعت کارآمدترین ترکیب نیرو، فضا و زمان است که میتواند برای متوقف کردن یک جسم متحرک استفاده شود. نرخ ایدهآل یک منحنی تقریباً مربعی است، که در آن یک نیروی ثابت در برابر بار مقاومت میکند تا زمانی که تا حد توقف کند شود.قدرت مورد نیاز یک نیروی خارجی برای حرکت دمپر به جهت گیری دمپر بستگی ندارد، بلکه فقط به سرعت نسبی قطعات آن بستگی دارد. یا احتمالاً موقعیت نسبی قطعات آن. و فاصله و سرعت نسبی به جهت گیری بستگی ندارد،


