هوپا، انجمن علم ایران

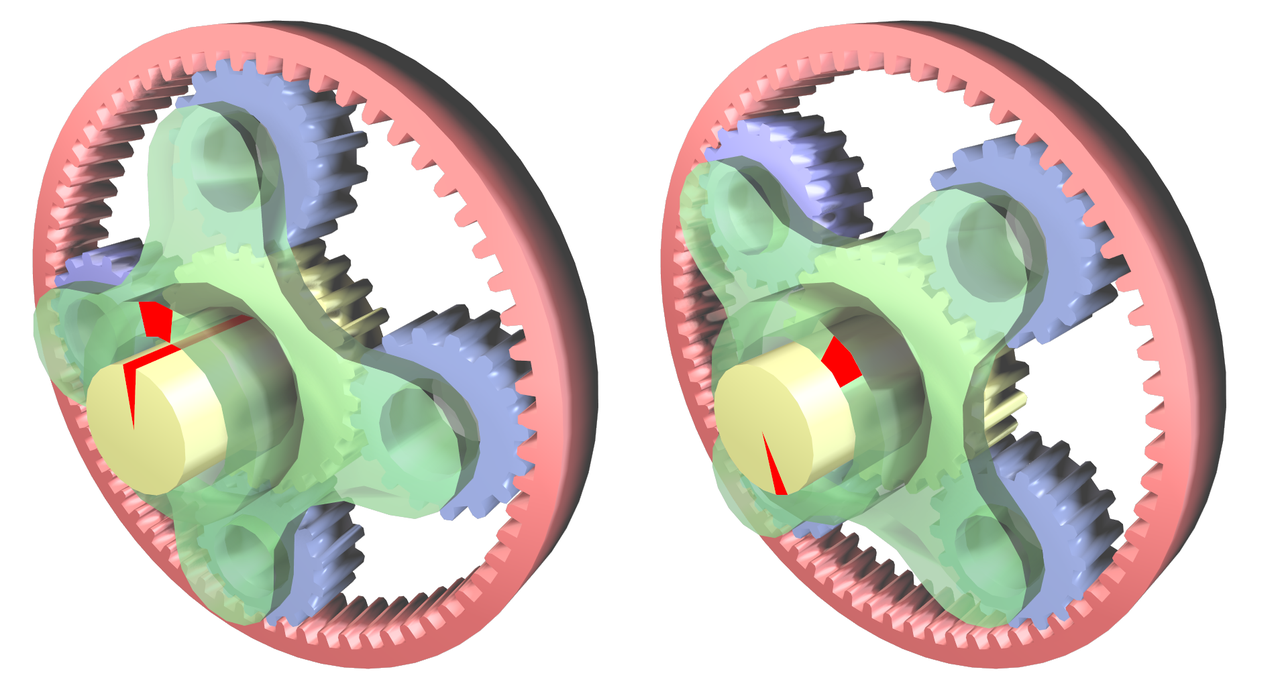
من سعی می کنم توزیع توان یک سیستم چرخ دنده سیاره ای،
برای یافتن توان خروجی، باید گشتاور حلقه های 5 و 6 را پیدا کنم. گشتاور و سرعت زاویه ای خورشید 1 مشخص است. همچنین من تمام سرعت های زاویه ای دیگر را دارم. من سعی می کنم روشی برای طراحی نمودار بدن آزاد این سیستم پیدا کنم.
اگر علامت مثبت در جهت عقربه های ساعت باشد، چگونه می توانم گشتاور T5 و T6 را به این نمودار بدنه آزاد اضافه کنم؟
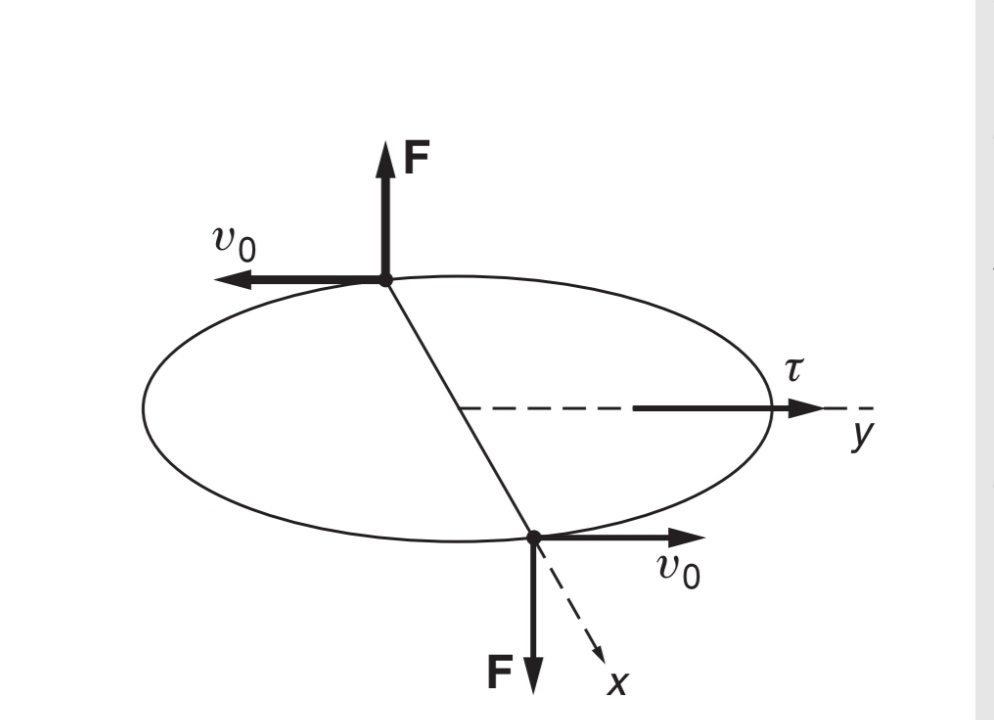
در این پاسخ، من از قرارداد علامت استفاده می‌کنم که گشتاورها و سرعت‌های زاویه‌ای در صورتی مثبت هستند که جهت آنها به سمت راست باشد (چپ نیز جایگزینی به همان اندازه معتبر برای این پاسخ خواهد بود) با استفاده از قانون دست راست، یعنی در جهت عقربه‌های ساعت دیده شود. اگر از سمت چپ نگاه کنید هر چرخ دنده ای که در جهت مخالف بچرخد سرعت زاویه ای منفی خواهد داشت.
رویکرد تعادلی
یک روش برای تعیین گشتاور در هر چرخ دنده ترسیم نمودار بدنه آزاد یک چرخ دنده با تمام نیروها (دنده های مشبک، واکنش شفت) و گشتاورهای خارجی (گشتاور شفت) اعمال شده بر روی آن چرخ دنده است. سپس با نادیده گرفتن نیروهای اینرسی، از تعادل برای نوشتن عبارتی در رابطه با نیروهای ناشناخته دندان و گشتاورهای خارجی استفاده کنید. نمونه ای از این کار برای چرخ دنده ای که با علامت 1 مشخص شده است انجام می شود:
توجه داشته باشید که جهت نیروها کاملا دلخواه است،
با اعمال تعادل، و حذف نیروی شفت (فقط به نیروهای دنده و گشتاورهای خارجی علاقه مند است)، به دست می آوریم:
$F_{II} = T_{in}/r_1$
که در آن r1 شعاع گام چرخ دنده (تقریبا) یا فاصله از مرکز دنده تا خط فشار است (دقیق است، اما اگر در نهایت به گشتاورهای خارجی علاقه مند هستید، لازم نیست). با تکرار این کار برای همه دنده‌ها، می‌توان گشتاورهای خارجی را به یکدیگر مرتبط کرد و نسبت‌های هر یک را نسبت به گشتاور ورودی تعیین کرد که علامت آن نسبت جهت گشتاور را نشان می‌دهد.
برای برخی از بدنه‌های چرخ دنده، فقط نیروهایی روی آن وارد می‌شوند. مثال زیر از یک قطار دنده باید این را برجسته کند:
وجه داشته باشید که چگونه دنده میانی هیچ گشتاور خارجی بر روی آن وارد نمی کند.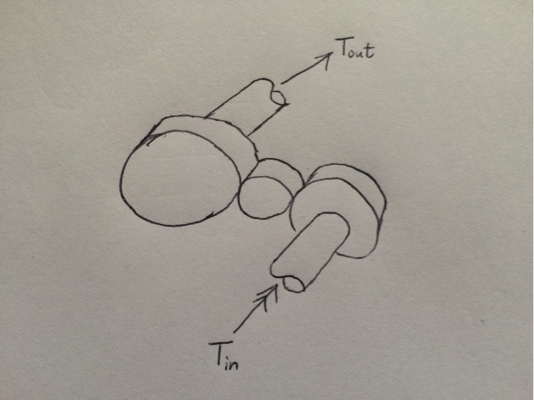
رویکرد قدرت مجازی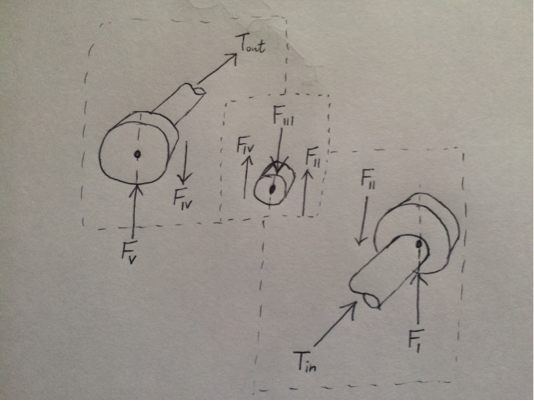
استفاده از روش دوم می تواند ساده تر باشد، به خصوص اگر سرعت های زاویه ای از قبل شناخته شده باشند. اول از همه، یک معادله جبری منفرد که سرعت های زاویه ای چرخ دنده ها را با گشتاورهای خارجی مرتبط می کند، باید به دست آید. برای قطارهای دنده ساده، این معادله فقط دو سرعت زاویه ای دارد و به شکل زیر است:
$\omega_{out} = G \omega_{in}$
که در آن G نسبت دنده ای است که باید تعیین شود. برای اکثر منظومه های سیاره ای، سه سرعت زاویه ای وجود دارد. مثالی که من از آن استفاده خواهم کرد قانون سرعت برای یک گیربکس ساده سیاره ای است:
$\omega_s = (1+R)\omega_c - R\omega_a$
که در آن زیرنویس‌های "s"، "c" و "a" به چرخ دنده‌های خورشید، حامل و حلقوی اشاره دارند. R نسبت دندانه های چرخ دنده حلقوی به دنده خورشیدی است.
اکنون، ما به یک معادله موازنه توان نیاز داریم: برق در = خاموش کردن. اینجاست که قرارداد علامت به کار می‌آید: از آنجایی که جهت‌های مرسوم گشتاور و سرعت زاویه‌ای یکسان هستند، ضرب گشتاور خارجی که روی یک چرخ دنده اعمال می‌شود در سرعت زاویه‌ای آن، مقدار توان را به شما می‌دهد. بنابراین، معادله تعادل قدرت مجموع تمام محصولات توان وارد شده برابر با صفر خواهد بود. یعنی به طور کلی:
$\sum_i T_i \omega_i = 0$
برای مثال من این است:
$T_c \omega_c + T_s \omega_s + T_a \omega_a=0$
برای یک قطار دنده ساده، جایگزینی معادله سرعت زاویه‌ای با معادله تعادل قدرت بسیار ساده است، اما برای معادلات سرعت زاویه‌ای با بیش از دو سرعت، بلافاصله اینطور نیست. برای حل چنین معادلاتی، باید یکی از سرعت های زاویه ای را روی صفر قرار دهید، مثل اینکه آن چرخ دنده را ثابت نگه دارید، به عنوان مثال:
ωa=0 را تنظیم کنید:
معادله: $\omega_s = (1+R)\omega_c$
تعادل قدرت:$T_c \omega_c + T_s \omega_s=0$
جایگزین Ang. Vel. معادله تعادل توان: $T_c/T_s = -(1+R)$
برای تنظیم سرعت دیگر روی صفر این کار را تکرار کنید.
به نظر می رسد که این تقلب با تنظیم اجباری سرعت های زاویه ای روی صفر است، اما همچنان معتبر است زیرا راه حل تعادل (یعنی مقادیر گشتاور خارجی) هرگز به سرعت های زاویه ای در ابتدا بستگی نداشت.
در نهایت، از هر روشی که استفاده شد، می توان یک بررسی سریع انجام داد تا ببیند آیا تمام گشتاورها تعادل جهانی را برآورده می کنند یا خیر. به لطف کنوانسیون نشانه، تعادل جهانی حاصل می شود اگر:$\sum_i T_i = 0$

درک من این است که در یک گیربکس سیاره ای، نیرو از طریق چهار مکانیسم در سیستم حرکت می کند: چرخ دنده حلقه ای، چرخ دنده سیاره ای، حامل سیاره ای و چرخ دنده خورشیدی. من سعی می کنم بفهمم چگونه می توان گشتاور ورودی به سیستم را با اندازه گیری آن تنها در یکی از این چهار نقطه محاسبه کرد.
ر مدل ذهنی من از مسئله، می‌دانم که انتقال نیرو از حلقه، از طریق سیارات و/یا حامل سیاره‌ای و به چرخ دنده خورشیدی رخ خواهد داد.
شهود من به من می گوید که اگر مقاومت در حامل سیاره ای بیشتر از مقاومت در چرخ دنده خورشیدی باشد، حامل سیاره ای نمی چرخد ​​و در عوض نیرو توسط چرخ دنده های سیارات منفرد (به جای حامل سیاره) منتقل می شود. در این مورد، آیا اندازه گیری گشتاور تجربه شده توسط حامل سیاره ای، گشتاور ورودی را اندازه گیری می کند؟
برای بیان این سوال به شکل ملموس تر، در این سیستم:
چرخ دنده حلقه (ورودی) (گشتاور نامشخص)
دنده خورشیدی (خروجی) (مقاومت ناشناخته ای دارد)
حامل سیاره ای (بر روی محفظه ثابت با سنسور گشتاور استاتیک بین)
آیا می توانم گشتاور تولید شده از چرخ دنده حلقه ای را از طریق سنسور گشتاور استاتیک در حامل سیاره ای اندازه گیری کنم؟
ه طور کلی، گشتاور به چرخ دنده های سیاره ای منفرد اعمال نمی شود، فقط به حاملی که آنها را نگه می دارد. مگر اینکه شما یک موتور مجزا به هر چرخ دنده سیاره ای متصل داشته باشید (از لحاظ فیزیکی ممکن است، اما به ندرت عملی است) احتمالا فقط 3 مکان دارید که باید گشتاور را بدانید: خورشید، حامل و حلقه. اگر در حال اندازه گیری گشتاور در چرخ دنده حلقه هستید، اگر تعداد دندانه های خورشید و چرخ دنده های حلقه را بدانید (Ns, Nr) می توانید سایر گشتاورها را محاسبه کنید:
$\tau_s = \tau_r \frac{N_s}{N_r}$
$\tau_c = -\tau_r \frac{N_r + N_s}{N_r}$

تلاش برای طراحی یک دنده سیاره ای با نسبت دنده 2:1، و مطمئن نیستم که چگونه شروع کنم. این چرخ دنده های سیاره ای تولید نمی کند، و من همچنین نمی دانم که چگونه یک چرخ دنده سیاره ای با نسبت 2:1 طراحی کنیم.
هنگام طراحی چرخ دنده های سیاره ای، سه نوع دنده مختلف برای طراحی وجود دارد:
چرخ دنده حلقوی، چرخ دنده داخلی اطراف چرخ دنده های دیگر
دنده خورشیدی، یک چرخ دنده خارجی در وسط مجموعه دنده
چرخ دنده های سیاره ای، چرخ دنده های بیرونی اطراف چرخ دنده خورشیدی، معمولاً سه یا چهار مورد از آنها وجود دارد
اول از همه، در مورد چرخ دنده های داخلی قابل توجه است. چرخ دنده های خورشیدی و سیاره ای که چرخ دنده های خارجی هستند (یعنی دندانه ها به سمت بیرون هستند) دقیقاً مانند هر نوع چرخ دنده دیگری هستند. با این حال، چرخ دنده آنولوس یک چرخ دنده داخلی است که دندانه ها به سمت داخل هستند. یک چرخ دنده داخلی ممکن است شبیه یک دایره باشد که یک چرخ دنده خارجی از داخل دایره کم شده است، و تقریباً همینطور است. فقط یک تفاوت جزئی در فاصله دندان ها از دایره گام وجود دارد. توجه نکردن به این تفاوت در دنده های داخلی می تواند منجر به برخورد نامطلوب دندانه های چرخ دنده قبل از مش بندی مناسب شود و باعث گیرکردن مجموعه دنده شود. بنابراین، اگر با خروجی چرخ دنده ها به صورت فایل های dxf مشکلی ندارید، پیشنهاد می کنم از ژنراتور دنده دکتر راینر هسمر استفاده کنید، زیرا به شما امکان می دهد هم چرخ دنده های خارجی و هم داخلی ایجاد کنید.
وقتی صحبت از طراحی واقعی این سه نوع چرخ دنده می شود، باید معادله زیر را که به عنوان قانون سرعت از آن یاد می کنم، رعایت کرد:
$\omega_C (1+\rho) = \omega_A \rho + \omega_S$
ωC سرعت چرخش حامل است که در تصویر بالا به رنگ سبز نشان داده شده است. ωA سرعت چرخش چرخ دنده حلقوی و ωS سرعت چرخش چرخ دنده خورشیدی است. سرعت چرخش همگی مثبت در یک جهت چرخش تعریف شده است. ρ نسبت تعداد دندانه های چرخ دنده حلقوی به تعداد دندانه های دنده خورشیدی است. شایان ذکر است که ρ نمی تواند کمتر یا مساوی 1 باشد.
اغلب، خارج از حامل، چرخ دنده حلقوی و چرخ دنده خورشیدی، یکی برای ثابت شدن در جای خود (ω=0)، یکی به عنوان ورودی و دیگری به عنوان خروجی انتخاب می شود (اما ممکن است دارای دو ورودی یا دو خروجی). با تثبیت یکی از سرعت‌های چرخش، می‌توان نسبت دنده را بین ورودی و خروجی تعیین کرد که به شرح زیر است:
حامل را ثابت کنید: $\omega_C = 0, \frac{\omega_S}{\omega_A} = -\rho$
حلقوی را ثابت کنید: $\omega_A = 0, \frac{\omega_S}{\omega_C} = \rho+1$
خورشید را ثابت کنید:$\omega_S = 0, \frac{\omega_A}{\omega_C} = 1+\frac{1}{\rho}$
اکنون موضوع انتخاب یکی از تنظیمات فوق است که نسبت دنده مناسب را به شما می دهد. گاهی اوقات به کمی آزمون و خطا نیاز دارد: به یک پیکربندی بچسبید و مقدار ρ را تعیین کنید. اگر ρ کمتر از یک یا خیلی نزدیک به یک است، تنظیم دیگری را امتحان کنید.
برای مورد شما، با نسبت دنده 2:1، بیایید پیکربندی زیر را امتحان کنیم:
ثابت: حامل
ورودی: خورشید
خروجی: حلقوی
توجه داشته باشید که در این پیکربندی$\frac{\omega_S}{\omega_A} = -\rho$، بنابراین ورودی و خروجی باید در جهت مخالف چرخش داشته باشند تا مقدار ρ مثبت بدست آید. فرض کنید ورودی در جهت "منفی" و خروجی در جهت "مثبت" می چرخد. از این رو:
$\frac{\omega_S}{\omega_A} = \frac{-2}{1} = -2$
ρ=2
مقدار ρ که بزرگتر از 1 است به دست می آید: به نظر می رسد این پیکربندی به خوبی کار می کند. اکنون وارد فاز دوم طراحی چرخ دنده سیاره ای می شویم: تعیین تعداد دندانه ها.
اول از همه، چرخ دنده های سیاره ای معمولاً به طور مساوی از یکدیگر فاصله دارند. برای رسیدن به این هدف، تعداد دندانه های هر دو چرخ دنده خورشیدی و حلقه باید مضرب تعداد سیارات باشد. در غیر این صورت، ممکن است هنگام مونتاژ چرخ دنده ها با هم مشکلاتی ایجاد شود. این فرآیندی است که ممکن است نیاز به آزمون و خطا داشته باشد، و حتی ممکن است نیاز به تغییر بسیار جزئی مقدار ρ داشته باشد تا آسان‌تر کردن تعداد دندان‌ها چند برابر شود.
در مثال ما فرض می کنیم که چهار چرخ دنده سیاره ای وجود دارد. بنابراین مشاهده می شود که دنده خورشیدی 31 (نه مضرب از 4) دندان مناسب نیست، اما یکی از دندانه های 32 (چند 4) مناسب است. اگر دنده خورشیدی 32 دندانه داشته باشد، دنده حلقوی دارای 32×ρ=64 دندانه خواهد بود. 64 نیز مضرب 4 است و بنابراین مناسب است.
هنگامی که تعداد دندانه های چرخ دنده های خورشیدی و حلقوی انتخاب شد،
تعداد دندانه های چرخ دنده سیاره با استفاده از فرمول زیر محاسبه می شود:
$\text{planet teeth} = \frac{\text{annulus teeth} - \text{sun teeth}}{2}$
به تقسیم بر دو توجه کنید: این بدان معنی است که تعداد دندانه های حلقه و چرخ دنده خورشیدی باید هر دو اعداد فرد یا هر دو عدد زوج باشند. اگر معلوم شد که اینطور نیست، دو برابر کردن تعداد دندانه های خورشید و چرخ دنده های حلقوی به سرعت مشکل را حل می کند. در مثال ما، تعداد دندانه های هر چرخ دنده سیاره ای 16 است.
با تعداد دندانه‌های انتخاب شده، بسته به اینکه دنده‌ها چقدر قوی هستند، اکنون یک ماژول یا گام قطری مناسب را انتخاب کنید، و آن مجموعه دنده‌های سیاره‌ای طراحی شده است.

اجازه دهید یک جسم صلب را در نظر بگیریم که از دو ذره به جرم m در دو طرف یک میله صلب بدون جرم به طول 2lتشکیل شده است.
فرض کنید که میله در فضای آزاد با تکانه زاویه ای Ls در امتداد جهت z می چرخد.
فرض کنید اکنون نیروهایی را بر دو جرم اعمال می کنم به طوری که نیروها همیشه عمود بر سرعت هر جرم برای همیشه هستند. همچنین نیروها برابر و مخالف هستند به طوری که مرکز جرم در حالت سکون باقی می ماند. پیکربندی اولیه نشان داده شده است.
من علاقه مند به تجسم حرکت متعاقب بدن هستم. برای انجام این کار، من بر بردار تکانه زاویه ای تمرکز کردم، زیرا اگر بدانم که جهت گیری سیستم را می شناسم، صفحه چرخش است.
من رابطه تکانه زاویه ای گشتاور را اعمال کردم و به این نتیجه رسیدم که بردار تکانه زاویه ای مطابق شکل زیر می چرخد.
من مطمئن نیستم که آیا این درست است. هر گونه راهنمایی لطفا
اگر تفسیر جسم صلب سرعت زاویه‌ای/تکانه زاویه‌ای را فراموش کنید، مسیرهای واقعی حرکت نقاط فقط دایره‌هایی روی کره هستند که توسط نقاط انتهایی میله که کره‌ای به شعاع l است و مرکز آن در مرکز قرار دارد، عبور می‌کنند. با جرم G. دایره هایی هستند که به سادگی از تقاطع کره با صفحات به دست می آیند. حرکت نقطه در امتداد چنین دایره ای یکنواخت است. این واقعیت از این واقعیت ناشی می شود که حرکت روی کره منحنی است تحت شتابی که همیشه بر کره مماس است، همیشه به همان اندازه و همیشه عمود بر جهت حرکت است. و تنها منحنی‌هایی که این شرط را برآورده می‌کنند، دایره‌هایی هستند که در بالا توضیح داده شد، که به طور یکنواخت طی شده‌اند.
اما، اگر هنوز می‌خواهید تفسیر سرعت زاویه‌ای را با جزئیات مرور کنید، اینجاست.
اول، من فکر می کنم که این وضعیت معادل یک میله چرخان در یک میدان گرانشی ثابت نیست.
از آنجایی که وضعیت توصیف شده در این مشکل یک وضعیت انتزاعی است، یعنی میله بدون جرم است، توده های نقطه اتصال و اجسام صلب نیست، برای اینکه به درستی آن را به عنوان یک مشکل بدنه صلب تلقی کنیم، ابتدا باید مدلی را برای نسخه بدنه صلب بنویسیم که عبارت است از مسئله برای یک جفت کره جامد با شعاع r که نشان دهنده نقاط جرمی است که توسط یک میله بدون جرم به هم متصل شده اند. سپس در صورت تمایل می توانید r=0 را تنظیم کنید و جواب نقاط جرم را بدست آورید.
ایده خوبی است که به این مشکل از سیستم مختصات$G \, \vec{e}_1, \, \vec{e}_2, \, \vec{e}_3$ نگاه کنیم که محکم به جسم صلب متصل شده است (و بنابراین با توجه به یک سیستم مختصات اینرسی جهانی در حال حرکت است). سیستم مختصات $G \, \vec{e}_1, \, \vec{e}_2, \, \vec{e}_3$غیر اینرسی است. فرض کنید مبدأ این سیستم مختصات در مرکز جرم G باشد، بردار واحد $\vec{e}_1$ با قطعه از G به یکی از نقاط جرمی تراز شده است، در حالی که دو بردار واحد دیگر $\vec{e}_2$ و $\vec{e}_3$ هستند. عمود بر $\vec{e}_1$ و عمود بر یکدیگر.
کره ها نسبت به هر محوری دارای گشتاور اینرسی $\frac{2}{5}mr^2$ هستند. از آنجایی که گشتاورهای اینرسی افزایشی هستند، گشتاور اینرسی نسبت به محور $G\,\vec{e}_1$ مقدار$I_1 = \frac{4}{5}mr^2$است. با قضیه محور موازی، گشتاورهای اینرسی نسبت به دو محور دیگر $G\,\vec{e}_2$ و $G\,\vec{e}_3$ یکسان و برابر با$I = I_1 + 2ml^2$ است.
به عبارت دیگر، ماتریس اینرسی در این سیستم مختصات ثابت جسم شکل می گیرد
$J = I_1 \, P_1 \, + I \, P_{23}$
که در آن P1 عملگر طرح ریزی متعامد از فضای سه بعدی به محور $G\vec{e}_1$ است، و P23 ماتریس طرح ریزی متعامد است که فضای سه بعدی را بر روی صفحه مختصاتی که توسط $\vec{e}_2$ و $\vec{e}_3$ کشیده شده است، ترسیم می کند.
$P_{1} \vec{e}_1 = \vec{e}_1 \,\,\,\,\, P_{1} \vec{e}_2 = 0, \,\,\,\,\, P_{23} \vec{e}_3 = 0$
$P_{23} \vec{e}_1 = 0, \,\,\,\,\, P_{23} \vec{e}_2 = \vec{e}_2, \,\,\,\,\, P_{23} \vec{e}_3 = \vec{e}_3$
در این سیسم مختصات، بردار سرعت توسط
$\vec{v} = \vec{\omega} \times (\,l\,\vec{e}_1\,) = l\, \vec{\omega} \times \vec{e}_1$
بنابراین، یک بردار واحد، عمود بر هر دو $l \, \vec{e}_1$ و $\vec{v}$ است
$\frac{ \big(\,\vec{\omega} \times \vec{e}_1 \,\big) \times \vec{e}_1}{|\vec{\omega} \times \vec{e}_1|}$
و بنابراین، دو نیروی با قدر ثابت F، همانطور که در تصویر ترسیم شده است، هستند
$\vec{F} \, = \, F \, \frac{ \big(\,\vec{\omega} \times \vec{e}_1 \,\big) \times \vec{e}_1}{|\vec{\omega} \times \vec{e}_1|} \,\,\, \text{ and } \,\,\, -\, \vec{F} \, = \, - \, F \, \frac{ \big(\,\vec{\omega} \times \vec{e}_1 \,\big)\times \vec{e}_1}{|\vec{\omega} \times \vec{e}_1|}$
نیروها به ترتیب در نقاطی با بردارهای موقعیت$\vec{r} = l \, \vec{e}_1$ و $- \, \vec{r} = -\, l \, \vec{e}_1$ اعمال می شوند. در نتیجه، گشتاورها باید باشند
$\begin{align}
\vec{r} \times \vec{F} \, =&\, l \, \vec{e}_1 \times \left(\, F \, \frac{ \big(\, \vec{\omega} \times \vec{e}_1\,\big) \times \vec{e}_1}{|\vec{\omega} \times \vec{e}_1|} \,\right) \, = \, l F \,\, \frac{\vec{e}_1 \times \Big( \vec{e}_1 \times \big(\, \vec{e}_1 \times \vec{\omega}\,\big)\Big)}{| \vec{e}_1 \times \vec{\omega}|} \\
=& \,-\, lF \,\, \frac{ \,\vec{e}_1 \times \vec{\omega}\,}{|\vec{e}_1 \times \vec{\omega}|}
\end{align}$
و$(-\vec{r}) \times (- \vec{F}) \, =\, \vec{r} \times \vec{F} \, = \, \,-\, lF \,\, \frac{\, \vec{e}_1 \times \vec{\omega}\,}{|\vec{e}_1 \times \vec{\omega}|}$
به ترتیب، بنابراین کل گشتاور اعمال شده بر روی بدنه است
$-\, 2lF \,\, \frac{\, \vec{e}_1 \times \vec{\omega}\,}{|\vec{e}_1 \times \vec{\omega}|}$
معادلات حرکت در قاب مرجع$G \, \vec{e}_1, \, \vec{e}_2, \, \vec{e}_3$ متصل به بدنه، همانطور که توضیح داده شد،
$\begin{align}
&\frac{d}{dt} J \, \vec{\omega} \, = \, \big(\,J \, \vec{\omega}\,\big) \times \vec{\omega} \, -\, 2lF \,\, \frac{\, \vec{e}_1 \times \vec{\omega}\,}{|\vec{e}_1 \times \vec{\omega}|}\\
&\frac{d}{dt} U^T \, = \, - \big(\,\vec{\omega} \times \cdot \,\big)\, U^T
\end{align}$

که در آن $\vec{\omega}$ بردار سرعت زاویه ای در قاب مختصات ثابت بدنه $G \, \vec{e}_1, \, \vec{e}_2, \, \vec{e}_3$ و ماتریس$U \, \in \, \text{SO}(3)$ ماتریس چرخشی است که هر مختصاتی را از قاب ثابت بدنه$G \, \vec{e}_1, \, \vec{e}_2, \, \vec{e}_3$ می گیرد. ,e⃗ 3 به مختصات مربوطه در سیستم مختصات جهان اینرسی، دومی نیز در مرکز جرم G متمرکز شده است. علامت گذاری $\big(\,\vec{\omega} \times \cdot \,\big)$ ماتریسی است که برآورده می کند.
$\big(\,\vec{\omega} \times \cdot \,\big) \,\vec{r} \, = \, \vec{\omega} \times \vec{r}$
برای هر بردار سه بعدی $\vec{r}$ در کادر ثابت بدنه.
توجه کنید که معادله اول (بردار) از معادله دوم (ماتریسی) جدا شده است، بنابراین آن را جداگانه حل می کنیم.
ابتدا اجازه دهید $\, \omega_1 \, \vec{e}_1 = P_1\, \vec{\omega}\,$ و$\,\vec{\omega}_{23} = P_{23}\, \vec{\omega}\,$را تنظیم کنیم. سپس
$\vec{\omega} = {\omega}_1 \, \vec{e}_1 \, + \, \vec{\omega}_{23}$
سپس
$J \, \vec{\omega} \,=\,I_1 \, P_1 \vec{\omega} \, + \, I P_{23} \, \vec{\omega} = I_1 \, \omega_1\, \vec{e}_1 \, + \, I\, \vec{\omega}_{23}$
و معادله می شود$\begin{align}
I_1 \, \frac{d\omega_1}{dt} \vec{e}_1 \, + \, I\, \frac{d}{dt}\vec{\omega}_{23} \, =& \,\big(\, I_1 \, \omega_1\, \vec{e}_1 \, + \, I\, \vec{\omega}_{23}\,\big) \times \big(\, \omega_1 \, \vec{e}_1 + \vec{\omega}_{23} \,\big)\\ & \, -\, 2lF \,\, \frac{\, \vec{e}_1 \times\big( {\omega}_1 \vec{e}_1 + \vec{\omega}_{23}\big)\,}{|\vec{e}_1 \times \big( {\omega}_1 \vec{e}_1 + \vec{\omega}_{23}\big)|}\\
=& \, \big(\, I_1 \, \omega_1\, \, - \, I\, \omega_1\,\big) \,\vec{e}_1 \times \vec{\omega}_{23} \, -\, 2lF \,\, \frac{\, \vec{e}_1 \times \vec{\omega}_{23}\,}{|\vec{e}_1 \times \vec{\omega}_{23}|}
\end{align}$
یا معادل آن،
$\begin{align}
I_1 \, \frac{d\omega_1}{dt} \vec{e}_1 \, + \, I\, \frac{d}{dt}\vec{\omega}_{23} \,
=& \, \left(\big(\, I_1 - I\,\big) \, \omega_1 \, - \,\, \frac{\, 2lF \,}{|\vec{e}_1 \times \vec{\omega}_{23}|}\right) \vec{e}_1 \times \vec{\omega}_{23}
\end{align}$
از قبل،$I = I_1 + 2ml^2$، بنابراین $I - I_1 = 2ml^2$، که معادله را می سازد.
$\begin{align}
I_1 \, \frac{d\omega_1}{dt} \vec{e}_1 \, + \, I\, \frac{d}{dt}\vec{\omega}_{23} \,
=& \, - \, \left( 2ml^2\, \omega_1 \, + \,\, \frac{\, 2lF \,}{|\vec{e}_1 \times \vec{\omega}_{23}|}\right) \vec{e}_1 \times \vec{\omega}_{23}
\end{align}$
سپس، اجازه دهید هنجار $|\vec{e}_1 \times \vec{\omega}_{23}|$ را ساده کنیم. طبق تعریف، $\vec{\omega}_{23}$طرح متعامد سرعت زاویه ای$\vec{\omega}$ بر روی صفحه مختصاتی است که توسط بردارهای مختصات $\vec{e}_2$ و $\vec{e}_3$که عمود بر بردار مختصات باقی مانده $\vec{e}_1$هستند. بنابراین،$\vec{e}_1$ بر$\vec{e}_1$عمود بر$\vec{\omega}_{23}$ است. معادل حاصل ضرب نقطه ای $\vec{e}_1 \cdot \vec{\omega}_{23} \, = \, 0$ است. از این رو هنجار است
$\begin{align}
|\vec{e}_1 \times \vec{\omega}_{23}| &= |\vec{e}_1| \, |\vec{\omega}_{23}| = |\vec{\omega}_{23}|
\end{align}$
و معادله را می توان در from نوشت
$\begin{align}
I_1 \, \frac{d\omega_1}{dt} \vec{e}_1 \, + \, I\, \frac{d}{dt}\vec{\omega}_{23} \,=& \, - \, \left( 2ml^2\, \omega_1 \, + \,\, \frac{\, 2lF \,}{|\vec{\omega}_{23}|}\right) \vec{e}_1 \times \vec{\omega}_{23}
\end{align}$
حال، از آنجایی که معادله دارای دو جزء متعامد است، یکی در امتداد$\vec{e}_1$ و دیگری موازی با$G \,\vec{e}_2 \, \vec{e}_3$، اجازه دهید هر دو طرف معادله را با$\vec{e}_1$ ضرب نقطه ای کنیم.
$\begin{align}
\vec{e}_1 \cdot \left( I_1 \, \frac{d\omega_1}{dt} \vec{e}_1 \, + \, I\, \frac{d}{dt}\vec{\omega}_{23}\right) \,=& \, - \, \vec{e}_1 \cdot \left( \, \left( 2ml^2\, \omega_1 \, + \,\, \frac{\, 2lF \,}{|\vec{\omega}_{23}|}\right) \vec{e}_1 \times \vec{\omega}_{23} \right)\\
&\\
I_1 \, \frac{d\omega_1}{dt} (\vec{e}_1 \cdot \vec{e}_1) \, + \, I\, \left(\vec{e}_1 \cdot \frac{d}{dt}\vec{\omega}_{23} \right) \,=& \, - \, \left( 2ml^2\, \omega_1 \, + \,\, \frac{\, 2lF \,}{|\vec{\omega}_{23}|}\right) \big(\, \vec{e}_1 \cdot ( \,\vec{e}_1 \times \vec{\omega}_{23} ) \big)\\
\end{align}$با این حال، با توجه به ویژگی های محصول متقاطع $\vec{e}_1$ عمود بر $\vec{e}_1 \times \vec{\omega}_{23}$ است، به این معنی که
$\big(\, \vec{e}_1 \cdot ( \,\vec{e}_1 \times \vec{\omega}_{23} ) \big) = 0$
در نتیجه به آن می رسیم
$I_1 \, \frac{d\omega_1}{dt} (\vec{e}_1 \cdot \vec{e}_1) \, + \, I\, \frac{d}{dt}(\vec{e}_1 \cdot \vec{\omega}_{23} ) \,= \, 0$
و از آنجایی که $(\vec{e}_1 \cdot \vec{\omega}_{23} ) = 0$ و $(\vec{e}_1 \cdot \vec{\omega}_{23} ) = 0$ نتیجه می گیریم که
$I_1 \, \frac{d\omega_1}{dt} = 0$
از آنجایی که فرض کرده ایم $I_1$ صفر نیست، تنها احتمال باقی مانده این است
$\frac{d\omega_1}{dt} = 0$
یعنی مولفه $\vec{e}_1$ سرعت زاویه ای ثابت است. اجازه دهید این ثابت را با $\omega_1^0$ نشان دهیم
معادله دیفرانسیل برداری برای سرعت زاویه ای به کاهش می یابد
$\begin{align}
I\, \frac{d}{dt}\vec{\omega}_{23} \,=& \, - \, \left( 2ml^2\, \omega_1^0 \, + \,\, \frac{\, 2lF \,}{|\vec{\omega}_{23}|}\right) \vec{e}_1 \times \vec{\omega}_{23}
\end{align}$
ساده‌سازی نهایی معادله از این نتیجه حاصل می‌شود که قدر$|\vec{\omega}_{23}|$ ثابت است. برای اثبات آن، با تفکیک قدر $|\vec{\omega}_{23}|$با توجه به زمان t به مجذور شروع می کنیم:
$\begin{align}
\frac{d}{dt} \left(\frac{1}{2} \,|\vec{\omega}_{23}|^2\right) \, =& \, \vec{\omega}_{23} \cdot \frac{d\vec{\omega}_{23}}{dt}\\
=& \, \vec{\omega}_{23} \cdot \left( - \, \frac{1}{I}\left( 2ml^2\, \omega_1^0 \, + \,\, \frac{\, 2lF \,}{|\vec{\omega}_{23}|}\right) \vec{e}_1 \times \vec{\omega}_{23} \right)\\
=& \, - \, \frac{1}{I}\left( 2ml^2\, \omega_1^0 \, + \,\, \frac{\, 2lF \,}{|\vec{\omega}_{23}|}\right) \big( \vec{\omega}_{23} \cdot ( \vec{e}_1 \times \vec{\omega}_{23}) \big)\\
=& \, 0
\end{align}$
زیرا با توجه به ویژگی های حاصلضرب متقاطع $|\vec{\omega}_{23}|$ عمود بر $\vec{e}_1 \times \vec{\omega}_{23}$ است. زنجیره هویت های اخیر تنها زمانی امکان پذیر است که
$\frac{1}{2} \,|\vec{\omega}_{23}|^2 = \text{const}$
یعنی قدر $|\vec{\omega}_{23}|$ نیز ثابت است. اجازه دهید این ثابت را با علامت گذاری کنیم
$\omega_{23}^0 = |\vec{\omega}_{23}|$
در نهایت، معادله دیفرانسیل برداری برای سرعت زاویه ای به معادله دیفرانسیل بردار ضریب ثابت خطی ساده می شود.
$\begin{align}
\frac{d}{dt}\vec{\omega}_{23} \,=& \, - \, \left( \frac{2ml^2}{I}\, \omega_1^0 \, + \,\, \frac{\, 2lF \,}{I \,{\omega}_{23}^0}\right) \vec{e}_1 \times \vec{\omega}_{23}
\end{align}$
در مجموع، کل سیستم به کاهش می یابد
$\begin{align}
&\vec{\omega} = {\omega_1^0} \,\vec{e}_1 + \,\vec{\omega}_{23}\\
&\omega_{23}^0 = |\vec{\omega}_{23}|\\
&I = \frac{4}{5}mr^2 \, + \, 2ml^2\\
&\nu_0 = - \, \left( \frac{2ml^2}{I}\, \omega_1^0 \, + \,\, \frac{\, 2lF \,}{I \,{\omega}_{23}^0}\right)\\
&\frac{d}{dt}\vec{\omega}_{23} \,= \, \nu_0\, \vec{e}_1 \times \vec{\omega}_{23}\\
&\frac{d}{dt} U^T \, = \, - \big(\,\vec{\omega} \times \cdot \,\big)\, U^T
\end{align}$
در این مرحله، می توانیم معادله دیفرانسیل برداری را برای $\vec{\omega}_{12}$ حل کنیم، جایی که جواب
$\vec{\omega}_{12} \, = \, \omega_{23}^0\cos(\nu_0 t)\,\vec{e}_2 \, + \, \omega_{23}^0\sin(\nu_0 t)\,\vec{e}_3$
و بنابراین سرعت کامل زاویه ای است
$\vec{\omega} \, = \, \omega_1^0\, \vec{e}_1 \, + \, \omega_{23}^0\cos(\nu_0 t)\,\vec{e}_2 \, + \, \omega_{23}^0\sin(\nu_0 t)\,\vec{e}_3$
در مورد شما $\omega_1^0 = 0$ (و در صورت تمایل می توانید r=0 را تنظیم کنید، یعنی جفت کره را به نقاط جرمی کوچک کنید) سرعت زاویه ای برابر است با
$\vec{\omega} \, = \, \omega_0\cos(\nu_0 t)\,\vec{e}_2 \, + \, \omega_0\sin(\nu_0 t)\,\vec{e}_3$

که در آن ω0 قدر ثابت سرعت زاویه ای است. همانطور که می بینید، $\vec{\omega}$ دایره ای را می پیماید که در صفحه مختصات $\,G \, \vec{e}_2 \, \vec{e}_3\,$، در مرکز G و شعاع ω0 قرار دارد. علاوه بر این، $\vec{\omega}$ از آن ها به طور یکنواخت، با فرکانس ثابت $\nu_0$ عبور می کند.