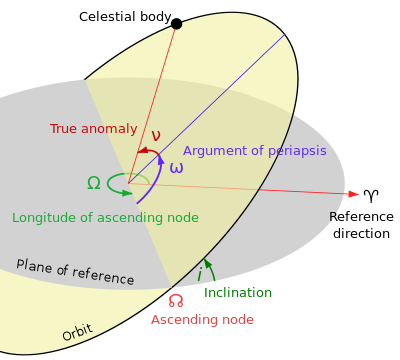
یافتن خروج از مرکز بیضی از زاویه آن با دایره
یک ماهواره کوچک به جرم m در مداری دایره ای به شعاع r0 با سرعت v0 به دور زمین می چرخد. در نقطه مشخصی از مدار خود، جهت حرکت ماهواره به طور ناگهانی با زاویه $θ = cos^{–1}(\frac35)$ با چرخش بردار سرعت آن در همان صفحه حرکت تغییر میکند، به طوری که سرعت ثابت میماند. در نتیجه، ماهواره به مدار بیضوی دور زمین می رود. نسبت سرعت در حضیض به سرعت در اوج برابر است با:
من این سوال را با حفظ تکانه زاویه ای و انرژی حل کردم. اما به روش دیگری با استفاده از فرمول سرعت در مدار بیضی در حضیض و اوج که توسط
$V_{max}=\sqrt{{\frac{GM}{a}} \frac{1+e}{1-e}}$
$V_{min}=\sqrt{{\frac{GM}{a}} \frac{1-e}{1+e}}$
با گرفتن نسبت، ثابت ها لغو می شوند و من باقی می مانم
$\frac{V_{max}}{V_{min}} =\frac{1+e}{1-e}$
بنابراین من باید با استفاده از زاویه $cos^{-1}(3/5)$ گریز از مرکز را پیدا کنم
آیا روشی برای محاسبه گریز از مرکز با استفاده از زاویه وجود دارد؟
می دانیم که انرژی یک ماهواره تنها به محور نیمه اصلی a مدار بیضی آن بستگی دارد. از آنجایی که انرژی ماهواره با تغییر ناگهانی از مدار دایره ای به مدار بیضوی تغییر نمی کند، نتیجه می شود که محور نیمه اصلی بیضی با شعاع دایره یکسان است.
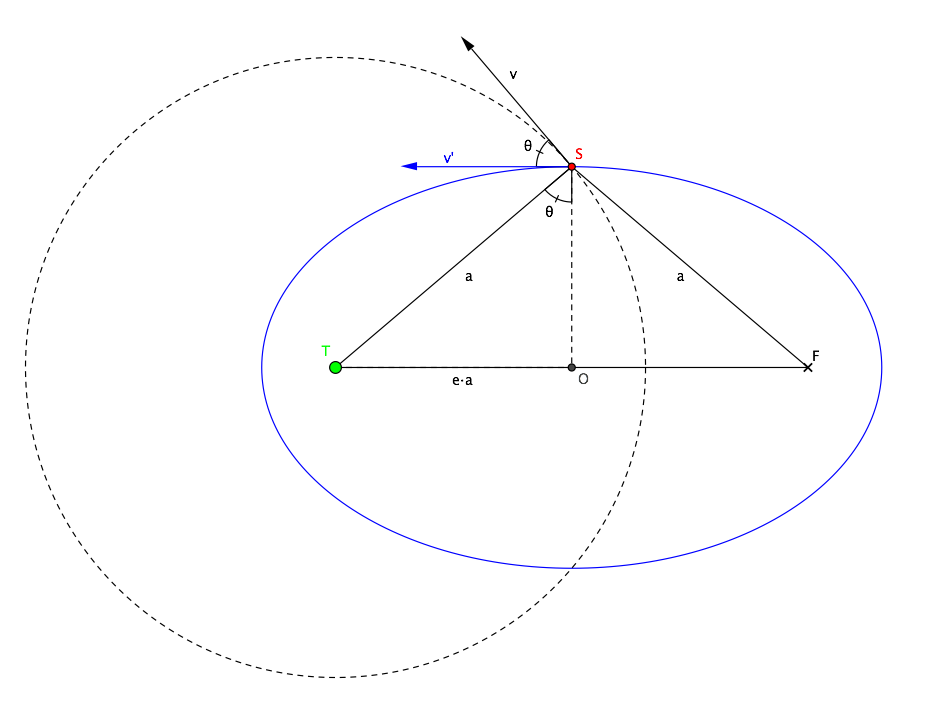
از این رو، هنگامی که سوئیچ رخ می دهد، ماهواره در فاصله a از زمین (کمک اول) و همچنین از کانون دوم (زیرا مجموع فواصل آن از کانون ها 2 a است): کانون ها و ماهواره یک مثلث متساوی الساقین را تشکیل می دهند. با اضلاع a، a و $2ea$ (با تعریف خروج از مرکز). زاویه θ نصف زاویه راس آن مثلث است و به این ترتیب به دست می آوریم:
${4\over5}=\sin\theta={ea\over a}=e,$
که دقیقا نتیجه شماست
زاویه بین بردار شعاع $\overrightarrow{r} $ (از کانون مدار) و بردار سرعت$\overrightarrow{v} $زاویه اوج"$\gamma \.$ است. (باید ذکر کنم که بسیاری از این اصطلاحات و نمادها در بین منابع و ارائههای مکانیک مداری متفاوت هستند.) "تکانه زاویهای مداری خاص$\overrightarrow{h} \ = \ \frac{ \ \overrightarrow{L}}{m}$ (بعضی این را $\overrightarrow{L}$ مینامند) سپس $\ \overrightarrow{h} \ = \ \overrightarrow{r} \times \overrightarrow{v} $ است. → که دارای قدر $r · v · \sin \gamma \ $است. (البته این یک کمیت حفظ شده است، یا، همانطور که مکانیک ها می گویند، یک "ثابت حرکت".) زاویه ای که اغلب به جای آن استفاده می شود، "زاویه مسیر پرواز" ϕ بین بردار سرعت و عمود بر آن است. بردار شعاع (یا "افقی محلی"). این زاویه ای است که در مسئله به صورت θ داده شده است، بنابراین $\cos \theta \ = \ \frac35 \ = \ \cos \phi \ = \ \sin \gamma \ \ .$
برای ویژگیهای مداری، مدار اولیه دایرهای با شعاع r0 «سرعت دایرهای» دارد.$\ v_0 \ = \ v_{circ} \ = \ \sqrt{\frac{GM}{r_0}} \ $. این با تغییر مدار تغییر نمیکند، بنابراین تکانه زاویهای خاص$\ h \ = \ r · v · \cos \phi \ = \ r_0 · \sqrt{\frac{GM}{r_0}} · \frac35 \ = \ \frac35 \sqrt{GMr_0} \\ ,$ میشود، در حالی که قبلا r⋅v⋅ بود. $\ r · v · \cos 0 \ = \ 1 · \sqrt{GMr_0} $. (از آنجایی که سرعت در r0 ثابت می ماند، محور نیمه اصلی مداری a = r0 [از مدار دایره ای] نیز تحت تأثیر قرار نمی گیرد
استخراج این رابطه مهمی که ما به آن نیاز داریم در بسیاری از متون مربوط به مکانیک مداری انجام شده است (من بیشتر به کتاب مبانی مکانیک آسمانی دانبی، ویرایش دوم، بخش 6.2 رفتم)، بنابراین در اینجا به جز این که بگویم، آن را بررسی نمی کنم. که با شروع
$\ \frac{d^2}{dt^2} \ \overrightarrow{r} \ = \ -\frac{GM}{r^3} \ \overrightarrow{r}$
(بردار شتاب گرانشی)، محصول برداری
$\ \overrightarrow{h} \times \frac{d^2}{dt^2} \ \overrightarrow{r} \ = \ -\frac{GM}{r^3} \ \overrightarrow{h} \times \overrightarrow{r} \ = \ -GM \ \frac{d}{dt} \left(\frac{\overrightarrow{r}}{r} \right)$
یکپارچه شده است، در نهایت برای تولید معادله قطبی برای مدار. رابطه ای که از این بیرون می آید $h^2 \ = \ GMa · (1 - e^2) \ \ ,$ است که e گریز از مرکز مداری است. برای مدار مورد بحث، این می شود
$\left( \ \frac35 \sqrt{GMr_0} \ \right)^2 \ = \ GM· r_0 · (1 - e^2) \ \ \Rightarrow \ \ \frac{9}{25} \ = \ (1 - e^2) \ \ \Rightarrow \ \ e \ = \ \frac45 \ \ .$
منابع دیگر عبارات مشتق شده مختلفی را ارائه می دهند. روی (حرکت مداری، ویرایش سوم، بخش 4.5) به عنوان مثال،
$e \ \ = \ \ \left[ \ 1 \ - \ \frac{r}{a^2} · (2a - r) · \sin^2 \gamma \ \right]^{1/2}$
$\rightarrow \ \ e \ \ = \ \ \left[ \ 1 \ - \ \frac{r_0}{r_0^2} · (2r_0 - r_0) · \left(\frac35 \right)^2 \ \right]^{1/2} \ \ = \ \ \left[ \ 1 \ - \ 1 · \frac{9}{25} \ \right]^{1/2} \ \ = \ \ \frac45 \ \ .$
(و، بله، تفاوت عبارات مشتق شده شما باید "1−e" باشد؛ در غیر این صورت، نتایج شما حتی برای یک مدار دایرهای [e=0] معنی نخواهد داشت.)..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering



رهام حسامی ترم هفتم مهندسی هوافضا