ترمودینامیک
-
rainbowjump
عضویت : یکشنبه ۱۴۰۰/۷/۴ - ۲۳:۳۶
پست: 31-
سپاس: 2
ترمودینامیک
سلام دوستان یه سوال داشتم اونم این که ما دقیقا از کجا میدونیم گرما از جسم گرم به جسم سرد شارش میکنه؟ وقتی ما یک جسم گرم و سرد رو کنار هم قرار می دیم جسم گرم سرد تر میشه و جسم سرد گرم تر خب حالا از کجا معلومه که این انرژی از جسم گرم به سرد بوده؟
-
amirzarei069
نام: amir zarei
عضویت : شنبه ۱۳۹۹/۱۱/۱۸ - ۱۷:۰۳
پست: 16-
سپاس: 3
- جنسیت:
تماس:
Re: ترمودینامیک
جواب شما قانون اول ترمودینامیک هست معلوم هست که اتم های موجود در اجسام گرم انرژی جنبشی بالاتری نسبت به اجسام سرد دارند. لذا برای حفظ تعادل حرارتی اتم های دارای انرژی جنبشی بالاتر سعی می کنند حرکت کنند و با اتم های دارای انرژی جنبشی پایین برخورد کنند. پس گرما از جسم گرم به جسم سرد منتقل می شود.طبق همین قانون هنگامی که یک جسم گرم را در تماس با جسم سرد قرار میدید گرما از گرم کننده به خنک کننده جریان می یابد. در نتیجه گرمتر معمولا خنک می شود و سردتر معمولا گرم می شود. در نهایت به همان دما می رسند و جریان گرما متوقف می شودما می توانیم فرآیندهای ترمودینامیکی را تصور کنیم که انرژی را حفظ می کنند به عنوان مثال، اگر یک جسم داغ را با یک جسم سرد در تماس قرار دهیم، مشاهده می کنیم که جسم داغ سرد می شود و جسم سرد گرم می شود تا زمانی که به تعادل برسد. انتقال گرما از جسم گرم به جسم سرد انجام می شود. اما میتوانیم سیستمی را تصور کنیم که در آن گرما از جسم سرد به جسم داغ منتقل میشود و چنین سیستمی قانون اول ترمودینامیک را نقض نمیکنه. جسم سرد سردتر و جسم گرم گرمتر می شود اما انرژی حفظ میشه
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: ترمودینامیک
آیا گرما (؟) می تواند از یک جسم سرد به جسم گرم جریان یابد؟
وقتی یک قاشق (استیل ضد زنگ) را در بستنی فرو می کنیم سرد می شود یا در همان دما می ماند؟ اگر اینطور باشد، آیا می توانیم بگوییم که گرما (؟) می تواند از اجسام سرد به گرم جریان یابد؟حرارت از قاشق به بستنی منتقل می شود و در نتیجه انرژی داخلی و در نتیجه دمای قاشق کاهش می یابد. برای انتقال حرارت از یک جسم سرد به یک جسم گرم، به یک سیکل تبرید (پمپ، اواپراتور، کمپرسور، شیر گاز و سیال کاری مناسب) نیاز دارید.از نظر تئوری، ممکن است گرما از یک جسم سرد به یک جسم گرمتر جریان یابد، اما احتمال وقوع آن تقریباً برابر با صفر است. این (از لحاظ نظری) به دلیل قانون دوم ترمودینامیک امکان پذیر است که می گوید آنتروپی در یک سیستم ایزوله تمایل به افزایش دارد. اما این قانون یک قانون اساسی نیست; بلکه یک قانون آماری است و به موضوع ترمودینامیک آماری تعلق دارد.
احتمال اینکه حرارت از قاشق به بستنی برود تقریباً 100٪ است. دلیل استفاده از قاشق های چوبی به جای قاشق فلزی این است که گرما از قاشق فلزی به بستنی سریعتر از قاشق چوبی می رود، زیرا فلز رسانای گرمایی بسیار بهتری نسبت به چوب است. بنابراین قاشق فلزی سریعتر از قاشق چوبی خنک می شود.گرما تنها به دلیل اختلاف دما انتقال انرژی است. گرما به طور طبیعی از دمای بالاتر به پایین تر جریان می یابد. برای اینکه گرما از دمای پایین به بالا (مثلاً یخچال یا تهویه مطبوع) جریان یابد، کار باید (توسط کمپرسور) انجام شود.
از آنجایی که دمای اولیه قاشق (دمای اتاق یا حدود 25 درجه سانتیگراد) بیشتر از دمای بستنی است (کمتر از 0 درجه سانتیگراد در جایی که شروع به ذوب شدن می کند)، گرما از قاشق به سمت بستنی جریان می یابد و دمای بستنی را کاهش می دهد. قاشق.
امیدوارم این کمک کند.گرما می تواند از اجسام سرد به گرم جریان یابد، به عنوان مثال، در یخچال و تهویه مطبوع رخ می دهد، اما نیاز به کار خارجی روی سیستم دارد. این کار لزوماً توسط یک "موتور حرارتی" (که می تواند چیزی شبیه به یک نیروگاه هسته ای باشد) تولید می شود که به دلیل انتقال گرما از یک جسم گرم (دیگر) به یک جسم سرد (دیگر) کار می کند. به طور کلی، گرما در جهتی جریان مییابد که به نفع دمای یکسانکننده است، یعنی به سمت تعادل ترمودینامیکی.
همچنین توجه داشته باشید که انتقال گرما از یک جسم سرد به یک جسم گرم منجر به کاهش آنتروپی سیستم می شود، اما جریان گرما در کار تامین کننده موتور حرارتی منجر به افزایش آنتروپی می شود، به طوری که آنتروپی کلی افزایش می یابد.
و بنابراین جهت جریان گرما فقط یک موضوع تعریف بود.
فقط بحث تعریف نیست. موضوع مشاهده است. هرگز مشاهده نمی شود که گرما به طور طبیعی یا خود به خود از یک ماده با دمای پایین به یک ماده با دمای بالا جریان یابد. برای اینکه این اتفاق بیفتد، باید کار انجام شود (مثلاً در مورد یخچال ها و پمپ های حرارتی).
قبل از تدوین قانون دوم، قانون اول را داشتیم. آن قانون بیانیه بقای انرژی است. اگر گرمای گرما از جسم سرد به گرم جریان یابد، گرمای از دست رفته توسط جسم سرد برابر با گرمای بدست آمده توسط جسم داغ خواهد بود و قانون اول برآورده می شود. اما از آنجایی که این هرگز اتفاق نمی افتد، قانون جدیدی لازم بود که چنین جریان گرمایی را غیرممکن کند.
اگرچه عبارت "برهان" نسبتاً ناخوشایند است، حداقل برای من، این درست است که وقتی گرما از سیستم گرمتر منتقل می شود، هم در آنتروپی و هم در انرژی داخلی (dU) سیستم داغ کاهش می یابد و یک افزایش آنتروپی و انرژی درونی سیستم سرد. تمایز مهم این است که انرژی داخلی حفظ می شود، اما آنتروپی اینطور نیست، مگر اینکه انتقال حرارت "برگشت پذیر" باشد.
کاهش انرژی داخلی سیستم گرم دقیقا برابر است با افزایش انرژی داخلی سیستم سرد، طبق قانون اول، برای تغییر کل انرژی داخلی صفر. از طرف دیگر، برای هر اختلاف محدود دما بین سیستم گرم و سرد، کاهش آنتروپی سیستم گرم کمتر از افزایش آنتروپی سیستم سرد است، برای تغییر آنتروپی کل بیشتر از صفر.
اگر سیستم های سرد و گرم مخازن حرارتی (منابع دمای ثابت و گیرنده گرما) باشند، تغییر آنتروپی سیستم گرم برابر است با
$\Delta S_{H}=-\frac{Q}{T_H}$
تغییر آنتروپی سیستم سرد است
$\Delta S_{C}=+\frac{Q}{T_L}$
کل تغییر آنتروپی است
$\Delta S_{tot}=+\frac{Q}{T_L}-\frac{Q}{T_H}$
توجه داشته باشید که برای همه $T_{H}>T_{L}$، ,$\Delta S_{tot}>0$.
بنابراین، جهت جریان گرما به دلیل تعریف است یا قانون دوم ترمودینامیک؟
خیر. جهت طبیعی جریان گرما از گرم به سرد یک واقعیت قابل مشاهده در طبیعت است. دومی طبیعت را دیکته نمی کند. قانون دوم طبیعت را منعکس می کند. قانون دوم این را می گوید
$\Delta S_{tot}=\Delta S_{sys}+\Delta S_{sur}\ge0$
جایی که علامت مساوی برای انتقال برگشت پذیر گرما اعمال می شود، یعنی زمانی که اختلاف بین TH و TL به صفر نزدیک شود.
اگر گرما از سرد به گرم جریان یابد، علائم تغییرات آنتروپی در دو معادله اول بالا معکوس میشود و در نتیجه$\Delta S_{tot}<0$ در نقض قانون دوم است..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering


 رهام حسامی ترم هفتم مهندسی هوافضا
رهام حسامی ترم هفتم مهندسی هوافضا
وقتی یک قاشق (استیل ضد زنگ) را در بستنی فرو می کنیم سرد می شود یا در همان دما می ماند؟ اگر اینطور باشد، آیا می توانیم بگوییم که گرما (؟) می تواند از اجسام سرد به گرم جریان یابد؟حرارت از قاشق به بستنی منتقل می شود و در نتیجه انرژی داخلی و در نتیجه دمای قاشق کاهش می یابد. برای انتقال حرارت از یک جسم سرد به یک جسم گرم، به یک سیکل تبرید (پمپ، اواپراتور، کمپرسور، شیر گاز و سیال کاری مناسب) نیاز دارید.از نظر تئوری، ممکن است گرما از یک جسم سرد به یک جسم گرمتر جریان یابد، اما احتمال وقوع آن تقریباً برابر با صفر است. این (از لحاظ نظری) به دلیل قانون دوم ترمودینامیک امکان پذیر است که می گوید آنتروپی در یک سیستم ایزوله تمایل به افزایش دارد. اما این قانون یک قانون اساسی نیست; بلکه یک قانون آماری است و به موضوع ترمودینامیک آماری تعلق دارد.
احتمال اینکه حرارت از قاشق به بستنی برود تقریباً 100٪ است. دلیل استفاده از قاشق های چوبی به جای قاشق فلزی این است که گرما از قاشق فلزی به بستنی سریعتر از قاشق چوبی می رود، زیرا فلز رسانای گرمایی بسیار بهتری نسبت به چوب است. بنابراین قاشق فلزی سریعتر از قاشق چوبی خنک می شود.گرما تنها به دلیل اختلاف دما انتقال انرژی است. گرما به طور طبیعی از دمای بالاتر به پایین تر جریان می یابد. برای اینکه گرما از دمای پایین به بالا (مثلاً یخچال یا تهویه مطبوع) جریان یابد، کار باید (توسط کمپرسور) انجام شود.
از آنجایی که دمای اولیه قاشق (دمای اتاق یا حدود 25 درجه سانتیگراد) بیشتر از دمای بستنی است (کمتر از 0 درجه سانتیگراد در جایی که شروع به ذوب شدن می کند)، گرما از قاشق به سمت بستنی جریان می یابد و دمای بستنی را کاهش می دهد. قاشق.
امیدوارم این کمک کند.گرما می تواند از اجسام سرد به گرم جریان یابد، به عنوان مثال، در یخچال و تهویه مطبوع رخ می دهد، اما نیاز به کار خارجی روی سیستم دارد. این کار لزوماً توسط یک "موتور حرارتی" (که می تواند چیزی شبیه به یک نیروگاه هسته ای باشد) تولید می شود که به دلیل انتقال گرما از یک جسم گرم (دیگر) به یک جسم سرد (دیگر) کار می کند. به طور کلی، گرما در جهتی جریان مییابد که به نفع دمای یکسانکننده است، یعنی به سمت تعادل ترمودینامیکی.
همچنین توجه داشته باشید که انتقال گرما از یک جسم سرد به یک جسم گرم منجر به کاهش آنتروپی سیستم می شود، اما جریان گرما در کار تامین کننده موتور حرارتی منجر به افزایش آنتروپی می شود، به طوری که آنتروپی کلی افزایش می یابد.
و بنابراین جهت جریان گرما فقط یک موضوع تعریف بود.
فقط بحث تعریف نیست. موضوع مشاهده است. هرگز مشاهده نمی شود که گرما به طور طبیعی یا خود به خود از یک ماده با دمای پایین به یک ماده با دمای بالا جریان یابد. برای اینکه این اتفاق بیفتد، باید کار انجام شود (مثلاً در مورد یخچال ها و پمپ های حرارتی).
قبل از تدوین قانون دوم، قانون اول را داشتیم. آن قانون بیانیه بقای انرژی است. اگر گرمای گرما از جسم سرد به گرم جریان یابد، گرمای از دست رفته توسط جسم سرد برابر با گرمای بدست آمده توسط جسم داغ خواهد بود و قانون اول برآورده می شود. اما از آنجایی که این هرگز اتفاق نمی افتد، قانون جدیدی لازم بود که چنین جریان گرمایی را غیرممکن کند.
اگرچه عبارت "برهان" نسبتاً ناخوشایند است، حداقل برای من، این درست است که وقتی گرما از سیستم گرمتر منتقل می شود، هم در آنتروپی و هم در انرژی داخلی (dU) سیستم داغ کاهش می یابد و یک افزایش آنتروپی و انرژی درونی سیستم سرد. تمایز مهم این است که انرژی داخلی حفظ می شود، اما آنتروپی اینطور نیست، مگر اینکه انتقال حرارت "برگشت پذیر" باشد.
کاهش انرژی داخلی سیستم گرم دقیقا برابر است با افزایش انرژی داخلی سیستم سرد، طبق قانون اول، برای تغییر کل انرژی داخلی صفر. از طرف دیگر، برای هر اختلاف محدود دما بین سیستم گرم و سرد، کاهش آنتروپی سیستم گرم کمتر از افزایش آنتروپی سیستم سرد است، برای تغییر آنتروپی کل بیشتر از صفر.
اگر سیستم های سرد و گرم مخازن حرارتی (منابع دمای ثابت و گیرنده گرما) باشند، تغییر آنتروپی سیستم گرم برابر است با
$\Delta S_{H}=-\frac{Q}{T_H}$
تغییر آنتروپی سیستم سرد است
$\Delta S_{C}=+\frac{Q}{T_L}$
کل تغییر آنتروپی است
$\Delta S_{tot}=+\frac{Q}{T_L}-\frac{Q}{T_H}$
توجه داشته باشید که برای همه $T_{H}>T_{L}$، ,$\Delta S_{tot}>0$.
بنابراین، جهت جریان گرما به دلیل تعریف است یا قانون دوم ترمودینامیک؟
خیر. جهت طبیعی جریان گرما از گرم به سرد یک واقعیت قابل مشاهده در طبیعت است. دومی طبیعت را دیکته نمی کند. قانون دوم طبیعت را منعکس می کند. قانون دوم این را می گوید
$\Delta S_{tot}=\Delta S_{sys}+\Delta S_{sur}\ge0$
جایی که علامت مساوی برای انتقال برگشت پذیر گرما اعمال می شود، یعنی زمانی که اختلاف بین TH و TL به صفر نزدیک شود.
اگر گرما از سرد به گرم جریان یابد، علائم تغییرات آنتروپی در دو معادله اول بالا معکوس میشود و در نتیجه$\Delta S_{tot}<0$ در نقض قانون دوم است..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering

آخرین ویرایش توسط rohamavation پنجشنبه ۱۴۰۱/۶/۳۱ - ۰۹:۵۹, ویرایش شده کلا 1 بار

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: ترمودینامیک
وقتی یک جسم سرد و گرم برای مدتی با یکدیگر در تماس باشند چه اتفاقی میافتد؟
اگر دو جسم در دماهای مختلف با یکدیگر تماس پیدا کنند، انرژی از جسم گرمتر (یعنی جسم با دمای بیشتر) به جسم سردتر (درجه حرارت پایین تر) منتقل می شود تا زمانی که هر دو جسم در یک دما باشند.یک متغیر ترمودینامیکی مفید به نام آنتروپی (S) وجود دارد.
یک فرآیند طبیعی به سمتی خواهد رفت که باعث آنتروپی می شود
سیستم به علاوه محیط ثابت بماند یا افزایش یابد.
ترمودینامیک شاخه ای از فیزیک است که به انرژی و کار یک سیستم می پردازد. ترمودینامیک فقط با پاسخ مقیاس بزرگ یک سیستم سروکار دارد که ما می توانیم آن را در آزمایشات مشاهده و اندازه گیری کنیم. در علم موشک، ترمودینامیک گاز بدیهی است که نقش مهمی در تجزیه و تحلیل سیستمهای پیشرانه و همچنین در درک جریانهای با سرعت بالا دارد. قانون اول ترمودینامیک رابطه بین اشکال مختلف انرژی موجود در یک سیستم (سینتیکی و پتانسیل)، کاری که سیستم انجام می دهد و انتقال گرما را تعریف می کند. قانون اول بیان می کند که انرژی در تمام فرآیندهای ترمودینامیکی حفظ می شود.
ما می توانیم فرآیندهای ترمودینامیکی را تصور کنیم که انرژی را حفظ می کنند اما هرگز در طبیعت رخ نمی دهند. به عنوان مثال، اگر یک جسم داغ را با یک جسم سرد در تماس قرار دهیم، مشاهده می کنیم که جسم داغ سرد می شود و جسم سرد گرم می شود تا زمانی که به تعادل برسد. انتقال گرما از جسم گرم به جسم سرد انجام می شود. اما میتوانیم سیستمی را تصور کنیم که در آن گرما از جسم سرد به جسم داغ منتقل میشود و چنین سیستمی قانون اول ترمودینامیک را نقض نمیکند. جسم سرد سردتر و جسم گرم گرمتر می شود، اما انرژی حفظ می شود. بدیهی است که ما در طبیعت با چنین سیستمی مواجه نیستیم و برای توضیح این مشاهدات و مشاهدات مشابه ترمودینامیک ها قانون دوم ترمودینامیک را پیشنهاد کردند. کلاسیوس، کلوین و کارنو اشکال مختلفی از قانون دوم را برای توصیف مسئله فیزیک خاصی که هر کدام در حال مطالعه بودند، پیشنهاد کردند. شرح قانون دوم بیان شده در این اسلاید برگرفته از کتاب درسی فیزیک هالیدی و رزنیک است. با تعریف یک متغیر حالت جدید به نام آنتروپی شروع می شود. آنتروپی دارای تفاسیر فیزیکی مختلفی است، از جمله بی نظمی آماری سیستم، اما برای اهداف ما، اجازه دهید آنتروپی را فقط یکی دیگر از ویژگی های سیستم، مانند آنتالپی یا دما، در نظر بگیریم.
قانون دوم بیان می کند که یک متغیر حالت مفید به نام آنتروپی S وجود دارد. تغییر در دلتای آنتروپی S برابر است با تقسیم دلتای انتقال حرارت Q بر دمای T.
برای یک فرآیند فیزیکی معین، آنتروپی ترکیبی سیستم و محیط ثابت باقی میماند، اگر بتوان فرآیند را معکوس کرد. اگر حالت اولیه و نهایی سیستم را با "i" و "f" نشان دهیم:
Sf = Si (فرایند برگشت پذیر)
نمونه ای از یک فرآیند برگشت پذیر در حالت ایده آل، اجبار جریان از طریق یک لوله منقبض است. ایده آل به معنای عدم تلفات لایه مرزی است. همانطور که جریان از طریق انقباض حرکت می کند، فشار، دما و سرعت تغییر می کند، اما این متغیرها در پایین دست انقباض به مقادیر اولیه خود باز می گردند. حالت گاز به شرایط اولیه خود باز می گردد و تغییر آنتروپی سیستم صفر است. مهندسان چنین فرآیندی را فرآیند ایزنتروپیک می نامند. ایزنتروپیک به معنای آنتروپی ثابت است.
قانون دوم بیان می کند که اگر فرآیند فیزیکی برگشت ناپذیر باشد، آنتروپی ترکیبی سیستم و محیط باید افزایش یابد. برای یک فرآیند برگشت ناپذیر، آنتروپی نهایی باید بیشتر از آنتروپی اولیه باشد:
Sf > Si (فرایند برگشت ناپذیر)
مثالی از یک فرآیند برگشت ناپذیر مشکلی است من گفتم . یک جسم داغ در تماس با یک جسم سرد قرار می گیرد. در نهایت، هر دو به دمای تعادل یکسانی دست می یابند. اگر اجسام را جدا کنیم، در دمای تعادل باقی می مانند و به طور طبیعی به دمای اولیه خود باز نمی گردند. فرآیند رساندن آنها به دمای یکسان غیر قابل برگشت است..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering


 رهام حسامی ترم هفتم مهندسی هوافضا
رهام حسامی ترم هفتم مهندسی هوافضا
اگر دو جسم در دماهای مختلف با یکدیگر تماس پیدا کنند، انرژی از جسم گرمتر (یعنی جسم با دمای بیشتر) به جسم سردتر (درجه حرارت پایین تر) منتقل می شود تا زمانی که هر دو جسم در یک دما باشند.یک متغیر ترمودینامیکی مفید به نام آنتروپی (S) وجود دارد.
یک فرآیند طبیعی به سمتی خواهد رفت که باعث آنتروپی می شود
سیستم به علاوه محیط ثابت بماند یا افزایش یابد.
ترمودینامیک شاخه ای از فیزیک است که به انرژی و کار یک سیستم می پردازد. ترمودینامیک فقط با پاسخ مقیاس بزرگ یک سیستم سروکار دارد که ما می توانیم آن را در آزمایشات مشاهده و اندازه گیری کنیم. در علم موشک، ترمودینامیک گاز بدیهی است که نقش مهمی در تجزیه و تحلیل سیستمهای پیشرانه و همچنین در درک جریانهای با سرعت بالا دارد. قانون اول ترمودینامیک رابطه بین اشکال مختلف انرژی موجود در یک سیستم (سینتیکی و پتانسیل)، کاری که سیستم انجام می دهد و انتقال گرما را تعریف می کند. قانون اول بیان می کند که انرژی در تمام فرآیندهای ترمودینامیکی حفظ می شود.
ما می توانیم فرآیندهای ترمودینامیکی را تصور کنیم که انرژی را حفظ می کنند اما هرگز در طبیعت رخ نمی دهند. به عنوان مثال، اگر یک جسم داغ را با یک جسم سرد در تماس قرار دهیم، مشاهده می کنیم که جسم داغ سرد می شود و جسم سرد گرم می شود تا زمانی که به تعادل برسد. انتقال گرما از جسم گرم به جسم سرد انجام می شود. اما میتوانیم سیستمی را تصور کنیم که در آن گرما از جسم سرد به جسم داغ منتقل میشود و چنین سیستمی قانون اول ترمودینامیک را نقض نمیکند. جسم سرد سردتر و جسم گرم گرمتر می شود، اما انرژی حفظ می شود. بدیهی است که ما در طبیعت با چنین سیستمی مواجه نیستیم و برای توضیح این مشاهدات و مشاهدات مشابه ترمودینامیک ها قانون دوم ترمودینامیک را پیشنهاد کردند. کلاسیوس، کلوین و کارنو اشکال مختلفی از قانون دوم را برای توصیف مسئله فیزیک خاصی که هر کدام در حال مطالعه بودند، پیشنهاد کردند. شرح قانون دوم بیان شده در این اسلاید برگرفته از کتاب درسی فیزیک هالیدی و رزنیک است. با تعریف یک متغیر حالت جدید به نام آنتروپی شروع می شود. آنتروپی دارای تفاسیر فیزیکی مختلفی است، از جمله بی نظمی آماری سیستم، اما برای اهداف ما، اجازه دهید آنتروپی را فقط یکی دیگر از ویژگی های سیستم، مانند آنتالپی یا دما، در نظر بگیریم.
قانون دوم بیان می کند که یک متغیر حالت مفید به نام آنتروپی S وجود دارد. تغییر در دلتای آنتروپی S برابر است با تقسیم دلتای انتقال حرارت Q بر دمای T.
برای یک فرآیند فیزیکی معین، آنتروپی ترکیبی سیستم و محیط ثابت باقی میماند، اگر بتوان فرآیند را معکوس کرد. اگر حالت اولیه و نهایی سیستم را با "i" و "f" نشان دهیم:
Sf = Si (فرایند برگشت پذیر)
نمونه ای از یک فرآیند برگشت پذیر در حالت ایده آل، اجبار جریان از طریق یک لوله منقبض است. ایده آل به معنای عدم تلفات لایه مرزی است. همانطور که جریان از طریق انقباض حرکت می کند، فشار، دما و سرعت تغییر می کند، اما این متغیرها در پایین دست انقباض به مقادیر اولیه خود باز می گردند. حالت گاز به شرایط اولیه خود باز می گردد و تغییر آنتروپی سیستم صفر است. مهندسان چنین فرآیندی را فرآیند ایزنتروپیک می نامند. ایزنتروپیک به معنای آنتروپی ثابت است.
قانون دوم بیان می کند که اگر فرآیند فیزیکی برگشت ناپذیر باشد، آنتروپی ترکیبی سیستم و محیط باید افزایش یابد. برای یک فرآیند برگشت ناپذیر، آنتروپی نهایی باید بیشتر از آنتروپی اولیه باشد:
Sf > Si (فرایند برگشت ناپذیر)
مثالی از یک فرآیند برگشت ناپذیر مشکلی است من گفتم . یک جسم داغ در تماس با یک جسم سرد قرار می گیرد. در نهایت، هر دو به دمای تعادل یکسانی دست می یابند. اگر اجسام را جدا کنیم، در دمای تعادل باقی می مانند و به طور طبیعی به دمای اولیه خود باز نمی گردند. فرآیند رساندن آنها به دمای یکسان غیر قابل برگشت است..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering

آخرین ویرایش توسط rohamavation پنجشنبه ۱۴۰۱/۶/۳۱ - ۰۹:۵۹, ویرایش شده کلا 1 بار

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: ترمودینامیک
از نظر تئوری، ممکن است گرما از یک جسم سرد به یک جسم گرمتر جریان یابد، اما احتمال وقوع آن تقریباً برابر با صفر است. این (از لحاظ نظری) به دلیل قانون دوم ترمودینامیک امکان پذیر است که می گوید آنتروپی در یک سیستم ایزوله تمایل به افزایش دارد.گرما تنها به دلیل اختلاف دما انتقال انرژی است. گرما به طور طبیعی از دمای بالاتر به پایین تر جریان می یابد. برای اینکه گرما از دمای پایین به بالا (مثلاً یخچال یا تهویه مطبوع) جریان یابد، کار باید (توسط کمپرسور) انجام شود.
از آنجایی که دمای اولیه قاشق (دمای اتاق یا حدود 25 درجه سانتیگراد) بیشتر از دمای بستنی است (کمتر از 0 درجه سانتیگراد در جایی که شروع به ذوب شدن می کند)، گرما از قاشق به سمت بستنی جریان می یابد و دمای بستنی را کاهش می دهد. قاشق.
واقع یک حس وجود دارد که در آن شما می توانید جریان گرما را از سیستمی با دمای پایین تر به سیستمی با دمای بالاتر دریافت کنید. گرما از سیستمی با دمای منفی به سیستمی با هر دمای مثبت جریان می یابد. این یک حیله نشان دادن است - سیستم های دمای منفی گرمتر از سیستم های دمای مثبت هستند. ترمودینامیکی بتا 1/kT را می توان به عنوان "سرما" در نظر گرفت و دمای منفی با عبور از سرمای صفر به جای دمای صفر به دست می آید.چرا چیزهای سرد کندتر از چیزهای داغ سرد می شوند؟
دو فنجان آب با حجم یکسان در فنجان ها وجود دارد که بر تبادل حرارت تأثیر نمی گذارد (یعنی فقط دمای هوا مهم است). یکی در مثلاً 80 درجه سانتیگراد و دیگری در 5 درجه سانتیگراد است. دمای هوای محیط 25 درجه سانتیگراد است.
بدیهی است که فنجان آب گرمتر سریعتر از فنجان سردتر خنک می شود، اما سوال من دقیقاً این است که چرا؟
باز هم فکر می کنم به قانون خنک سازی نیوتن مربوط می شود و نه چیزهای دیگر. یکی از دوستان من فکر می کند که بیشتر به ترمودینامیک مربوط می شود، مانند ظرفیت گرمایی ویژه که در دماهای مختلف متفاوت است.
اختلاف دما یک چیز است. قانون خنک کننده نیوتن این را نشان می دهد. با این حال؛ روش های مختلفی برای سرمایش و گرمایش وجود دارد. علاوه بر رسانایی، انتقال حرارت از همرفت (سیالات) و تابش نیز وجود دارد. مواد همچنین دارای رسانایی حرارتی هستند به این معنی که مواد مختلف گرما و سرد می شوند. این رسانایی نیز وابسته به دما است. در انتقال فاز قابل توجه است (مثلاً رسانایی یخ/آب/بخار را مقایسه کنید - یخ رسانایی حرارتی بالاتری دارد، بنابراین با گفته شما مخالفت می کند، اما پس از آن همرفتی وجود ندارد، به همین دلیل است که آب سرد می تواند سردتر از یخ باشد).
در یک محیط با تابش کم، یک جسم معمولاً دارای اتلاف گرمای خالص ناشی از تابش است که باعث میشود جسم سرد کندتر از سرد شدن یک جسم گرم گرم شود. در یک روز آفتابی سرد، این بیانیه درست نخواهد بود. چیزهای سرد سریعتر از چیزهای گرم سرد می شوند.
اتعاریف
سرعت تغییر دمای جسم جامد با جرم m (kg) و ظرفیت گرمایی ویژه $\tilde{C}_p$ و$dT/dt$ به صورت زیر نوشته شده است.
$m \tilde{C}_p\ {dT}/{dt} = \dot{q}$
اصطلاح$\dot{q}$ سرعتی است که در آن گرما وارد (برای گرم کردن) یا خروج (برای خنک کردن) جسم میشود.
برای شروع، فرض کنید شی در ابتدا در $T_o$ است و محیط اطراف در ثابت$T_s$ نگه داشته می شود.
انواع جریان گرما
گرما می تواند با تابش به سیال اطراف (گاز یا مایع) وارد یا خارج شود. نرخ تابش متناسب با توان چهارم دمای مطلق$\dot{q}_r \propto T^4$ است. نرخ کلی اولیه انتقال حرارت به ترتیب اول به صورت زیر بیان می شود.
$\dot{q}_{rT} \propto |T_o^4 - T_s^4|$
شما می توانید از این برای تعیین دمای اولیه جسم استفاده کنید که در آن جسم سرد جریان گرمای تشعشعی بیشتری از محیط اطراف دریافت می کند تا جسم گرم که توسط جریان گرمای تشعشعی به اطراف آزاد می شود. بنابراین، می توانید تعیین کنید که در چه مواردی یک جسم سرد یا گرم در همان دماهای هوا سریعتر از یک جسم گرم تغییر دما می دهد. توجه داشته باشید که یک خلاء دارای دمای $T_a = 0$ است و بنابراین تابش ورودی به جسم ندارد. در این حالت، جسم گرم و "سرد" هر دو خنک می شوند.
گرما می تواند از طریق جابجایی به جسم وارد یا خارج شود، زمانی که محیط اطراف سیال است (گاز یا مایع). سرعت انتقال حرارت با اختلاف دما متناسب است. با استفاده از همان فرآیند بالا، متوجه خواهید شد که نرخ خالص انتقال حرارت توسط همرفت به صورت زیر تعیین می شود.
$\dot{q}_{hT} \propto |T_o - T_s|$
از این موضوع می آموزیم که تا زمانی که اختلاف دمای جسم و سیال اطراف یکسان باشد، یک جسم گرم یا سرد با همرفت با همان سرعت سرد یا گرم می شود.
در نهایت، گرما می تواند از طریق رسانایی در محیط، جسم را به محیط اطراف وارد یا خارج کند. این با یک گرادیان دما$dT_s/dz$در محیط اطراف اتفاق میافتد. سیال معمولاً گرادیان دما را به خوبی حفظ نمی کند. گرادیان از بین می رود و جریان به صورت همرفتی است. بنابراین بیان این جمله که می خواهید رسانایی در محیط اطراف را در نظر بگیرید شبیه به این است که بگوییم شما محیط را نیز به عنوان یک جامد تعریف می کنید. نرخ خالص جریان رسانا به صورت زیر نوشته شده است.
$\dot{q}_{kT} \propto |{dT_s}/{dz}|$
تجزیه و تحلیل ترکیبی معادله نهایی به شکل زیر خواهد بود.
$m \tilde{C}_p\ {dT_o}/{dt} = \sigma A \left( \epsilon_s T_s^4 - \epsilon_o T_o^4 \right) + h_s A \left(T_s - T_o\right) - k_s A\ {dT_s}/{dz}$
اصطلاحات مختلف عبارتند از ضریب Stefan-Boltzmann σ، سطح جسم A، ضریب همرفت hs، و هدایت حرارتی ks. این معادله میزان تغییر دمای جسم را در هر نقطه از زمان مشخص می کند. علائم +/- طوری تنظیم می شوند که وقتی جسم گرمتر از محیط اطراف است، جسم خنک می شود (و بالعکس). این یک معادله نسبتا سخت است که معمولاً با در نظر گرفتن تنها یکی از سه حالت (تابش، همرفت یا هدایت) در یک زمان حل میشود. همچنین فرض می کند که جسم به طور یکنواخت گرم یا سرد می شود. حالتی که یک شیب حرارتی در جسم جامد دارید، معادله دیگری است.
به عنوان یک قانون کلی، سرعت تغییر دما (سرد شدن) یک جسم داغ را نمی توان سریعتر (یا کندتر) از سرعت تغییر دما (گرم شدن) یک جسم سرد بیان کرد. سرعت انتقال حرارت به نوع محیط اطراف (خلاء، سیال یا جامد)، دمای محیط و نوع انتقال حرارت (تابش، همرفت یا هدایت) بستگی دارد..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering


 رهام حسامی ترم هفتم مهندسی هوافضا
رهام حسامی ترم هفتم مهندسی هوافضا
از آنجایی که دمای اولیه قاشق (دمای اتاق یا حدود 25 درجه سانتیگراد) بیشتر از دمای بستنی است (کمتر از 0 درجه سانتیگراد در جایی که شروع به ذوب شدن می کند)، گرما از قاشق به سمت بستنی جریان می یابد و دمای بستنی را کاهش می دهد. قاشق.
واقع یک حس وجود دارد که در آن شما می توانید جریان گرما را از سیستمی با دمای پایین تر به سیستمی با دمای بالاتر دریافت کنید. گرما از سیستمی با دمای منفی به سیستمی با هر دمای مثبت جریان می یابد. این یک حیله نشان دادن است - سیستم های دمای منفی گرمتر از سیستم های دمای مثبت هستند. ترمودینامیکی بتا 1/kT را می توان به عنوان "سرما" در نظر گرفت و دمای منفی با عبور از سرمای صفر به جای دمای صفر به دست می آید.چرا چیزهای سرد کندتر از چیزهای داغ سرد می شوند؟
دو فنجان آب با حجم یکسان در فنجان ها وجود دارد که بر تبادل حرارت تأثیر نمی گذارد (یعنی فقط دمای هوا مهم است). یکی در مثلاً 80 درجه سانتیگراد و دیگری در 5 درجه سانتیگراد است. دمای هوای محیط 25 درجه سانتیگراد است.
بدیهی است که فنجان آب گرمتر سریعتر از فنجان سردتر خنک می شود، اما سوال من دقیقاً این است که چرا؟
باز هم فکر می کنم به قانون خنک سازی نیوتن مربوط می شود و نه چیزهای دیگر. یکی از دوستان من فکر می کند که بیشتر به ترمودینامیک مربوط می شود، مانند ظرفیت گرمایی ویژه که در دماهای مختلف متفاوت است.
اختلاف دما یک چیز است. قانون خنک کننده نیوتن این را نشان می دهد. با این حال؛ روش های مختلفی برای سرمایش و گرمایش وجود دارد. علاوه بر رسانایی، انتقال حرارت از همرفت (سیالات) و تابش نیز وجود دارد. مواد همچنین دارای رسانایی حرارتی هستند به این معنی که مواد مختلف گرما و سرد می شوند. این رسانایی نیز وابسته به دما است. در انتقال فاز قابل توجه است (مثلاً رسانایی یخ/آب/بخار را مقایسه کنید - یخ رسانایی حرارتی بالاتری دارد، بنابراین با گفته شما مخالفت می کند، اما پس از آن همرفتی وجود ندارد، به همین دلیل است که آب سرد می تواند سردتر از یخ باشد).
در یک محیط با تابش کم، یک جسم معمولاً دارای اتلاف گرمای خالص ناشی از تابش است که باعث میشود جسم سرد کندتر از سرد شدن یک جسم گرم گرم شود. در یک روز آفتابی سرد، این بیانیه درست نخواهد بود. چیزهای سرد سریعتر از چیزهای گرم سرد می شوند.
اتعاریف
سرعت تغییر دمای جسم جامد با جرم m (kg) و ظرفیت گرمایی ویژه $\tilde{C}_p$ و$dT/dt$ به صورت زیر نوشته شده است.
$m \tilde{C}_p\ {dT}/{dt} = \dot{q}$
اصطلاح$\dot{q}$ سرعتی است که در آن گرما وارد (برای گرم کردن) یا خروج (برای خنک کردن) جسم میشود.
برای شروع، فرض کنید شی در ابتدا در $T_o$ است و محیط اطراف در ثابت$T_s$ نگه داشته می شود.
انواع جریان گرما
گرما می تواند با تابش به سیال اطراف (گاز یا مایع) وارد یا خارج شود. نرخ تابش متناسب با توان چهارم دمای مطلق$\dot{q}_r \propto T^4$ است. نرخ کلی اولیه انتقال حرارت به ترتیب اول به صورت زیر بیان می شود.
$\dot{q}_{rT} \propto |T_o^4 - T_s^4|$
شما می توانید از این برای تعیین دمای اولیه جسم استفاده کنید که در آن جسم سرد جریان گرمای تشعشعی بیشتری از محیط اطراف دریافت می کند تا جسم گرم که توسط جریان گرمای تشعشعی به اطراف آزاد می شود. بنابراین، می توانید تعیین کنید که در چه مواردی یک جسم سرد یا گرم در همان دماهای هوا سریعتر از یک جسم گرم تغییر دما می دهد. توجه داشته باشید که یک خلاء دارای دمای $T_a = 0$ است و بنابراین تابش ورودی به جسم ندارد. در این حالت، جسم گرم و "سرد" هر دو خنک می شوند.
گرما می تواند از طریق جابجایی به جسم وارد یا خارج شود، زمانی که محیط اطراف سیال است (گاز یا مایع). سرعت انتقال حرارت با اختلاف دما متناسب است. با استفاده از همان فرآیند بالا، متوجه خواهید شد که نرخ خالص انتقال حرارت توسط همرفت به صورت زیر تعیین می شود.
$\dot{q}_{hT} \propto |T_o - T_s|$
از این موضوع می آموزیم که تا زمانی که اختلاف دمای جسم و سیال اطراف یکسان باشد، یک جسم گرم یا سرد با همرفت با همان سرعت سرد یا گرم می شود.
در نهایت، گرما می تواند از طریق رسانایی در محیط، جسم را به محیط اطراف وارد یا خارج کند. این با یک گرادیان دما$dT_s/dz$در محیط اطراف اتفاق میافتد. سیال معمولاً گرادیان دما را به خوبی حفظ نمی کند. گرادیان از بین می رود و جریان به صورت همرفتی است. بنابراین بیان این جمله که می خواهید رسانایی در محیط اطراف را در نظر بگیرید شبیه به این است که بگوییم شما محیط را نیز به عنوان یک جامد تعریف می کنید. نرخ خالص جریان رسانا به صورت زیر نوشته شده است.
$\dot{q}_{kT} \propto |{dT_s}/{dz}|$
تجزیه و تحلیل ترکیبی معادله نهایی به شکل زیر خواهد بود.
$m \tilde{C}_p\ {dT_o}/{dt} = \sigma A \left( \epsilon_s T_s^4 - \epsilon_o T_o^4 \right) + h_s A \left(T_s - T_o\right) - k_s A\ {dT_s}/{dz}$
اصطلاحات مختلف عبارتند از ضریب Stefan-Boltzmann σ، سطح جسم A، ضریب همرفت hs، و هدایت حرارتی ks. این معادله میزان تغییر دمای جسم را در هر نقطه از زمان مشخص می کند. علائم +/- طوری تنظیم می شوند که وقتی جسم گرمتر از محیط اطراف است، جسم خنک می شود (و بالعکس). این یک معادله نسبتا سخت است که معمولاً با در نظر گرفتن تنها یکی از سه حالت (تابش، همرفت یا هدایت) در یک زمان حل میشود. همچنین فرض می کند که جسم به طور یکنواخت گرم یا سرد می شود. حالتی که یک شیب حرارتی در جسم جامد دارید، معادله دیگری است.
به عنوان یک قانون کلی، سرعت تغییر دما (سرد شدن) یک جسم داغ را نمی توان سریعتر (یا کندتر) از سرعت تغییر دما (گرم شدن) یک جسم سرد بیان کرد. سرعت انتقال حرارت به نوع محیط اطراف (خلاء، سیال یا جامد)، دمای محیط و نوع انتقال حرارت (تابش، همرفت یا هدایت) بستگی دارد..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering

آخرین ویرایش توسط rohamavation پنجشنبه ۱۴۰۱/۶/۳۱ - ۰۹:۵۹, ویرایش شده کلا 1 بار

- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3286-
سپاس: 5494
- جنسیت:
تماس:
Re: ترمودینامیک
آیا دمای منفی در چرخه کارنو مثالی متضاد از قانون دوم ترمودینامیک به دست می دهد؟با قضیه کارنو، کارایی چرخه کارنو است
$\eta=1-\frac{T_C}{T_H}$
که در آن TC، TH به ترتیب دمای مطلق مخزن سرد و مخزن گرم هستند. از آنجایی که TC>0، این به معنای $\eta < 1$ است، بنابراین عبارت کلوین را نتیجه می گیرد: "هیچ فرآیندی امکان پذیر نیست که در آن تنها نتیجه آن جذب گرما از یک مخزن و تبدیل کامل آن به کار باشد."
با این حال، من فکر می کنم در آن دوره آنها دمای منفی را نمی دانند، اگر $T_C=300K $و$ T_H=−300K$ را بگذاریم، به راحتی می توان$\eta=2$ را بدست آورد. به نظر می رسد که این یک مثال متضاد از قانون دوم ترمودینامیک است.پاسخ کوتاه: وقتی $T_H<0,T_C>0$نمی توانید یک چرخه برگشت پذیر $\delta S_{cycle}=0$ بسازید. بنابراین عبارت کارایی صدق نمی کند.
برای پاسخ کامل من باید از طریق استخراج بازده چرخه کارنو بگذریم. طبق معمول، باید به علائم توجه زیادی کرد. تغییرات انرژی در بخاری و کولر مربوط به تغییرات آنتروپی آنهاست:
$\delta E_H=T_H\delta S_H,\quad \delta E_C=T_C\delta S_C$
بخاری انرژی را از دست می دهد، در حالی که کولر آن را دریافت می کند:
$\delta E_H < 0,\quad \delta E_C >0$
بنابراین کار انجام شده توسط یک بدنه کاری که انرژی را از بخاری به خنک کننده منتقل می کند:
$\delta A = -\delta E_H - \delta E_C > 0$
راندمان یک چرخه رابطه ای از کار انجام شده $\delta A>0$ با انرژی از دست رفته توسط بخاری است $-\delta E_H>0$
$\eta = \frac{\delta A}{-\delta E_H} = 1 + \frac{\delta E_C}{\delta E_H}=1 + \frac{T_C}{T_H}\frac{\delta S_C}{\delta S_H}$
در حالت "معمولی": $T_H>0, T_C>0$، در نتیجه، داریم:
$\delta S_H<0,\quad \delta S_C>0$
و ما مثالی از یک چرخه معکوس (چرخه کارنو) ارائه می دهیم که بنابراین باید از آن تبعیت کرد:
$\delta S_{cycle} = \delta S_H+\delta S_C = 0 \quad \Rightarrow \quad \frac{\delta S_C}{\delta S_H} = -1$
که منجر به فرمول معمول می شود.
اگر بخاری دارای دمای منفی باشد:$T_H<0, T_C>0$ خواهیم داشت:
$\delta S_H > 0,\quad \delta S_C>0$
بنابراین هیچ راهی برای ایجاد چرخه با $\delta S_{cycle}=0$ وجود ندارد. تنها چیزی که می توانید بگویید این است که:
$\frac{\delta S_C}{\delta S_H}>0 \quad \Rightarrow \quad \frac{T_C}{T_H}\frac{\delta S_C}{\delta S_H}<0 \quad \Rightarrow \quad \eta<1$
برای حل این موضوع، میتوانیم به سادگی از طریق استخراج بازده کارنو، با در نظر گرفتن این احتمال که TH ممکن است منفی باشد، مرور کنیم. به دلایلی هرگز نمی توانم بدون ترسیم نمودار به موتورهای حرارتی فکر کنم.
موتور گرمایی
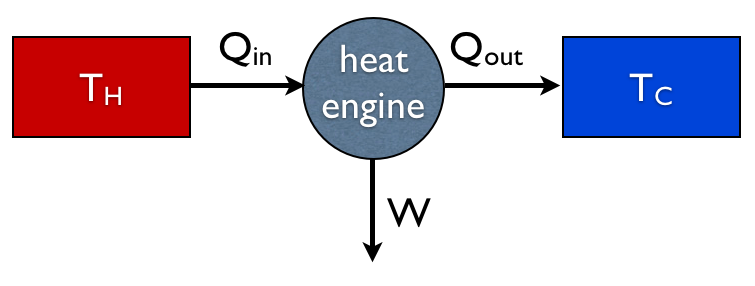 یک موتور حرارتی معمولی.
یک موتور حرارتی معمولی.
موتور مقداری گرما $Q_\text{in}$ را از یک مخزن در دمای TH می گیرد و مقداری کار W را خروجی می دهد و همچنین مقداری گرما Quut را به مخزن در دمای TC دفع می کند.
قانون اول می گوید $Q_\text{in} = W + Q_\text{out}$. قانون دوم می گوید که مقدار کل آنتروپی باید افزایش یابد. آنتروپی مخزن داغ $\frac{1}{T_H}Q_\text{in}$ کاهش می یابد و آنتروپی مخزن سرد$\frac{1}{T_C}Q_\text{out}$ افزایش می یابد. (کار W بر آنتروپی کل تأثیر نمی گذارد. کار انرژی بدون آنتروپی است).
بنابراین کل تغییر آنتروپی$\frac{1}{T_C}Q_\text{out} - \frac{1}{T_H}Q_\text{in}$ است. راندمان زمانی به حداکثر می رسد که این مقدار روی صفر تنظیم شود، که منجر به راندمان کارنو می شود.
$W_\text{max} = \left( 1- \frac{T_C}{T_H}\right) Q_\text{in}.$
حالا بیایید تصور کنیم که TH منفی است و ببینیم این تصور من چگونه تغییر می کند.
اولین چیزی که باید به آن توجه کرد این است که اکنون، وقتی گرما را از مخزن داغ حذف می کنیم، آنتروپی آن همچنان به میزان $-\frac{1}{T_H}Q_\text{in}$ تغییر می کند. اما این در حال حاضر یک تغییر مثبت است، به دلیل علامت منفی TH. شما می توانید $\frac{1}{T} = \frac{\partial S}{\partial U}$ را به عنوان مقداری در نظر بگیرید که با اضافه شدن مقدار کمی گرما، آنتروپی یک سیستم تغییر می کند. انرژی ذخیره شده در یک مخزن با دمای منفی "می خواهد" به گرما تبدیل شود، به این معنا که حذف گرما به جای کاهش آنتروپی آن را افزایش می دهد.
اکنون، ما هنوز میتوانیم دقیقاً همان استدلال قبلی را طی کنیم، و هنوز هم میتوانیم دریافت کنیم
$W_\text{max} = \left( 1- \frac{T_C}{T_H}\right) Q_\text{in},$،
و همانطور که اشاره کردید، این بزرگتر از 1 خواهد بود. اما توجه داشته باشید که در این مورد،$Q_\text{out} = Q_\text{in}-W_\text{out} < 0$. در مثال شما که در آن $\eta=2$ داریم.و$Q_\text{out} = -Q_\text{in}$
در پاسخ Kostya فرض شده است که $Q_\text{out}$ باید مثبت باشد، به همین دلیل است که او نتیجه می گیرد که موتوری با این کارایی نمی تواند وجود داشته باشد. اما من می خواهم با در نظر گرفتن ارزش اسمی آن رویکرد متفاوتی داشته باشم: کارآمدترین موتور در این شرایط موتوری است که در واقع گرما را از مخزن سرد خارج می کند:
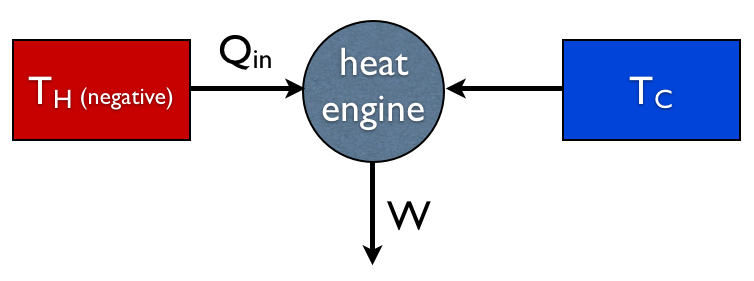
یک موتور حرارتی فوق کارآمد که با یک مخزن دمای منفی کار می کند. توجه داشته باشید که گرما را از هر دو مخزن خارج می کند.
اکنون می توانیم مقدار مشخصی از بازدهی بیشتر از یک را احساس کنیم. اگر$\eta>1$ به این معنی است که W بزرگتر از Qin است. اما این مشکلی ندارد زیرا در این شرایط بخشی از انرژی از مخزن سرد می آید. با قانون دوم مشکلی وجود ندارد، زیرا ما این را با تنظیم صریح افزایش آنتروپی روی 0 به دست آوردیم.
من می خواهم به عقب برگردم و چیزی را که قبلاً به آن اشاره کردم روشن کنم: می توانید گرما را از یک مخزن با دمای منفی خارج کنید و برخلاف گفته کلوین مستقیماً آن را به کار تبدیل کنید. یعنی این موتور امکان پذیر است:
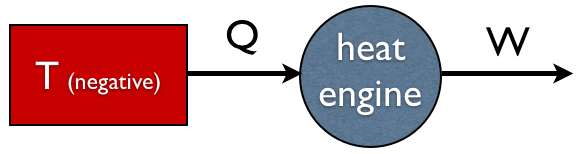
یک موتور حرارتی که گرمای دمای منفی را مستقیماً به کار تبدیل می کند.
اما این منافاتی با قانون دوم ندارد. موتور فوق حداکثر کارایی را ندارد و مقدار آنتروپی$-\frac{1}{T}Q$ تولید می کند که باز هم مثبت است زیرا T منفی است.
شما نمی توانید از آن برای ساخت یک ماشین حرکت دائمی استفاده کنید، زیرا دمای مخزن دمای منفی با حذف گرما از آن کاهش می یابد، تا زمانی که دمای آن به منهای بی نهایت برسد (که در زمان محدود انجام می دهد)، در این مرحله آن را انجام می دهد. به مثبت بودن تغییر خواهد کرد و به کاهش ادامه خواهد داد. این احتمالاً کاملاً غیرمعمول به نظر می رسد، بنابراین بخش مربوط به آن را در زیر ببینید.
بنابراین نتیجه همه اینها این است که بله، ممکن است η بزرگتر از 1 باشد اگر TH<0 باشد، اما این یک مثال متضاد با قانون دوم نیست و اجازه ساخت یک موبایل دائمی را نمی دهد. بیانیه کلوین قبل از آگاهی از دماهای منفی نوشته شده است، همانطور که شما می گویید، و برای اینکه برای چنین سیستم هایی صادق باشد، باید به گونه ای اصلاح شود که "هیچ فرآیندی ممکن نیست که تنها نتیجه آن جذب گرما از یک مخزن با مثبت باشد. دما و تبدیل کامل آن به کار."
چرا دما به -∞ کاهش می یابد و سپس مثبت می شود؟
در نپاسخ قبلی این پاسخ گفتم که برای ایجاد یک مخزن دمای منفی نیاز به کار دارید. این تا حدی درست است، اما من فکر میکنم استدلال زیر بهتر است.
با ذکر این نکته شروع می کنیم
$\frac{1}{T} = \frac{\partial S}{\partial U},$
که در آن U انرژی داخلی یک سیستم و S آنتروپی آن است. برای اکثر سیستم ها منحنی S(U) چیزی شبیه به این است:
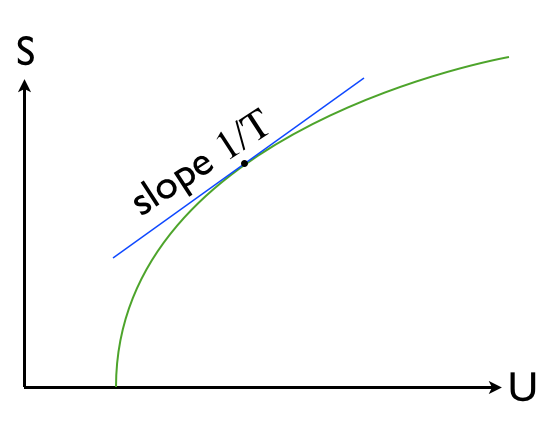
: منحنی S(U) برای یک جسم معمولی با ظرفیت حرارتی محدود.
می بینید که با حذف گرما از سیستم (کاهش U)، شیب$1/T$ افزایش می یابد (یعنی T کاهش می یابد) تا زمانی که در نقطه ای با U محدود (انرژی حالت پایه)، آنتروپی صفر و شیب بینهایت می شود. (یا T صفر می شود). این یک نتیجه اساسی از مکانیک آماری است که منحنی S(U) باید مقعر باشد، به این معنی که $1/T$ همیشه باید با افزایش U. Ty افزایشی نداشته باشد.
از نظر ظاهری، S و U هر دو نامحدود هستند.
با این حال، برای برخی از سیستمها (آنهایی که میتوانید وارونگی جمعیت داشته باشید) فقط میتوانند مقدار محدودی انرژی در خود نگه دارند، و برای آن سیستمها منحنی بیشتر شبیه این است:
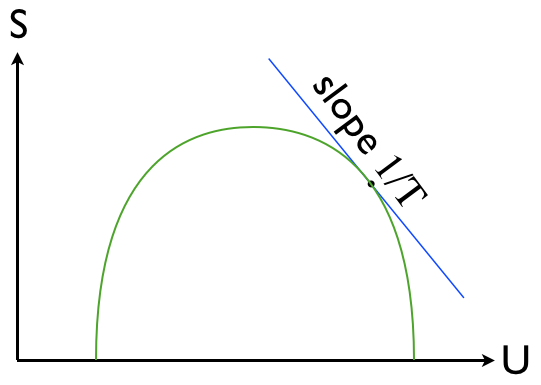 منحنی S(U) برای سیستمی که می تواند دمای منفی داشته باشد.
منحنی S(U) برای سیستمی که می تواند دمای منفی داشته باشد.
می بینید که این سیستم ها می توانند دماهای منفی داشته باشند، به این معنی که انرژی داخلی U در سمت راست پیک در S است. با حذف گرما از چنین سیستمی، $1/T$ افزایش می یابد تا زمانی که از صفر عبور کند و دوباره مثبت شود. که مربوط به کاهش -∞ T است، سپس به +∞ تغییر می کند و به کاهش ادامه می دهد.
بنابراین همانطور که انرژی را از یک مخزن با دمای منفی حذف می کنید، به ناچار آن را به یک مخزن با دمای مثبت طبیعی نزدیک می کنید. این دلیل اساسی است که چرا نمیتوانید یک ماشین حرکت دائمی با استفاده از مخازن دمای منفی بسازید: در نهایت ایدهآلسازی دمای ثابت باید از بین برود و مخزن دمای منفی شما به یک مخزن دمای مثبت تبدیل شود.
برعکس، برای ایجاد مخزن دمای منفی در وهله اول، باید انرژی را در آن صرف کنید. یک سیستم با منحنی S(U) که در شکل 4 نشان داده شده است، معمولاً در همان دمای (مثبت) محیط اطراف خود شروع می شود، به این معنی که انرژی داخلی U آن در سمت چپ قله در منحنی S خواهد بود. برای منفی کردن دما، باید با استفاده از یک پمپ حرارتی (مشابه شکل 2 اما با تمام فلش ها در جهت مخالف) در آن انرژی قرار دهید. در اصل، شما باید آن را آنقدر گرم کنید که دمای آن بی نهایت و سپس منفی شود. بنابراین اگرچه ممکن است کاملاً معجزهآسا به نظر برسد که گرمای دمای منفی میتواند 100% بدون تولید گرما به کار تبدیل شود، باید در نظر داشته باشید که سیستمهای دمای منفی چیز بسیار خاصی هستند که (تا آنجا که من میدانم) وجود ندارند. در طبیعت، و شما نمی توانید بدون استفاده از حداقل کاری که می توانید با استفاده از یک موتور حرارتی از آن استخراج کنید، یکی بسازید.
آیا گرما نباید از مخزن دمای منفی H به مخزن دمای مثبت C جریان یابد؟
اگر از موتور حرارتی برای استخراج کار استفاده نمی کردیم، بله، این کار را می کرد. همانطور که امیدواریم به وضوح از شکل 5 بالا مشاهده کنید، دمای منفی گرمتر از دمای مثبت است. اما نکته این است که ما فقط یک جریان خود به خودی گرما را در نظر نمی گیریم، بلکه کارآمدترین راه را برای استخراج کار از مخازن با استفاده از یک ماشین فرضی در نظر می گیریم.
ممکن است نگاهی دوباره به شکل 1 که یک موتور حرارتی معمولی را نشان می دهد کمک کند. در اینجا ما گرمایی داریم که از یک مخزن گرم خارج می شود و به مخزن سرد می رود. اما گرمایی که وارد مخزن سرد می شود کمتر از گرمای خارج شده از مخزن گرم است، زیرا مقداری از آن به کار تبدیل می شود. اگر TH را در حالی که Qin ثابت نگه داریم، افزایش دهیم، موتور می تواند کارآمدتر عمل کند، بنابراین $Q_\text{out}$ کاهش می یابد. اگر TH را بینهایت کنیم (یعنی $1/T_H=0$، بنابراین مخزن داغ درست در اوج منحنی S(U) در بالا قرار دارد) آنگاه $Q_\text{out}$ صفر می شود، زیرا موتور حرارتی با حداکثر کارآمدی بازده 1 دارد و می تواند گرما را در آن تبدیل کند. $T_\infty$ بدون تولید گرما کار کند. (به یک معنا، کار گرما با دمای بی نهایت است.)
اگر انرژی مخزن داغ را بیش از این افزایش دهیم، به طوری که دمای آن منفی شود (گذر از پیک روی منحنی S(U))، حداکثر بازده ممکن بیشتر از 1 و$Q_\text{out}$ منفی می شود. توجه داشته باشید که در این حالت موتور حرارتی گرما را از هر دو مخزن خارج می کند..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering


 رهام حسامی ترم هفتم مهندسی هوافضا
رهام حسامی ترم هفتم مهندسی هوافضا
$\eta=1-\frac{T_C}{T_H}$
که در آن TC، TH به ترتیب دمای مطلق مخزن سرد و مخزن گرم هستند. از آنجایی که TC>0، این به معنای $\eta < 1$ است، بنابراین عبارت کلوین را نتیجه می گیرد: "هیچ فرآیندی امکان پذیر نیست که در آن تنها نتیجه آن جذب گرما از یک مخزن و تبدیل کامل آن به کار باشد."
با این حال، من فکر می کنم در آن دوره آنها دمای منفی را نمی دانند، اگر $T_C=300K $و$ T_H=−300K$ را بگذاریم، به راحتی می توان$\eta=2$ را بدست آورد. به نظر می رسد که این یک مثال متضاد از قانون دوم ترمودینامیک است.پاسخ کوتاه: وقتی $T_H<0,T_C>0$نمی توانید یک چرخه برگشت پذیر $\delta S_{cycle}=0$ بسازید. بنابراین عبارت کارایی صدق نمی کند.
برای پاسخ کامل من باید از طریق استخراج بازده چرخه کارنو بگذریم. طبق معمول، باید به علائم توجه زیادی کرد. تغییرات انرژی در بخاری و کولر مربوط به تغییرات آنتروپی آنهاست:
$\delta E_H=T_H\delta S_H,\quad \delta E_C=T_C\delta S_C$
بخاری انرژی را از دست می دهد، در حالی که کولر آن را دریافت می کند:
$\delta E_H < 0,\quad \delta E_C >0$
بنابراین کار انجام شده توسط یک بدنه کاری که انرژی را از بخاری به خنک کننده منتقل می کند:
$\delta A = -\delta E_H - \delta E_C > 0$
راندمان یک چرخه رابطه ای از کار انجام شده $\delta A>0$ با انرژی از دست رفته توسط بخاری است $-\delta E_H>0$
$\eta = \frac{\delta A}{-\delta E_H} = 1 + \frac{\delta E_C}{\delta E_H}=1 + \frac{T_C}{T_H}\frac{\delta S_C}{\delta S_H}$
در حالت "معمولی": $T_H>0, T_C>0$، در نتیجه، داریم:
$\delta S_H<0,\quad \delta S_C>0$
و ما مثالی از یک چرخه معکوس (چرخه کارنو) ارائه می دهیم که بنابراین باید از آن تبعیت کرد:
$\delta S_{cycle} = \delta S_H+\delta S_C = 0 \quad \Rightarrow \quad \frac{\delta S_C}{\delta S_H} = -1$
که منجر به فرمول معمول می شود.
اگر بخاری دارای دمای منفی باشد:$T_H<0, T_C>0$ خواهیم داشت:
$\delta S_H > 0,\quad \delta S_C>0$
بنابراین هیچ راهی برای ایجاد چرخه با $\delta S_{cycle}=0$ وجود ندارد. تنها چیزی که می توانید بگویید این است که:
$\frac{\delta S_C}{\delta S_H}>0 \quad \Rightarrow \quad \frac{T_C}{T_H}\frac{\delta S_C}{\delta S_H}<0 \quad \Rightarrow \quad \eta<1$
برای حل این موضوع، میتوانیم به سادگی از طریق استخراج بازده کارنو، با در نظر گرفتن این احتمال که TH ممکن است منفی باشد، مرور کنیم. به دلایلی هرگز نمی توانم بدون ترسیم نمودار به موتورهای حرارتی فکر کنم.
موتور گرمایی
 یک موتور حرارتی معمولی.
یک موتور حرارتی معمولی.موتور مقداری گرما $Q_\text{in}$ را از یک مخزن در دمای TH می گیرد و مقداری کار W را خروجی می دهد و همچنین مقداری گرما Quut را به مخزن در دمای TC دفع می کند.
قانون اول می گوید $Q_\text{in} = W + Q_\text{out}$. قانون دوم می گوید که مقدار کل آنتروپی باید افزایش یابد. آنتروپی مخزن داغ $\frac{1}{T_H}Q_\text{in}$ کاهش می یابد و آنتروپی مخزن سرد$\frac{1}{T_C}Q_\text{out}$ افزایش می یابد. (کار W بر آنتروپی کل تأثیر نمی گذارد. کار انرژی بدون آنتروپی است).
بنابراین کل تغییر آنتروپی$\frac{1}{T_C}Q_\text{out} - \frac{1}{T_H}Q_\text{in}$ است. راندمان زمانی به حداکثر می رسد که این مقدار روی صفر تنظیم شود، که منجر به راندمان کارنو می شود.
$W_\text{max} = \left( 1- \frac{T_C}{T_H}\right) Q_\text{in}.$
حالا بیایید تصور کنیم که TH منفی است و ببینیم این تصور من چگونه تغییر می کند.
اولین چیزی که باید به آن توجه کرد این است که اکنون، وقتی گرما را از مخزن داغ حذف می کنیم، آنتروپی آن همچنان به میزان $-\frac{1}{T_H}Q_\text{in}$ تغییر می کند. اما این در حال حاضر یک تغییر مثبت است، به دلیل علامت منفی TH. شما می توانید $\frac{1}{T} = \frac{\partial S}{\partial U}$ را به عنوان مقداری در نظر بگیرید که با اضافه شدن مقدار کمی گرما، آنتروپی یک سیستم تغییر می کند. انرژی ذخیره شده در یک مخزن با دمای منفی "می خواهد" به گرما تبدیل شود، به این معنا که حذف گرما به جای کاهش آنتروپی آن را افزایش می دهد.
اکنون، ما هنوز میتوانیم دقیقاً همان استدلال قبلی را طی کنیم، و هنوز هم میتوانیم دریافت کنیم
$W_\text{max} = \left( 1- \frac{T_C}{T_H}\right) Q_\text{in},$،
و همانطور که اشاره کردید، این بزرگتر از 1 خواهد بود. اما توجه داشته باشید که در این مورد،$Q_\text{out} = Q_\text{in}-W_\text{out} < 0$. در مثال شما که در آن $\eta=2$ داریم.و$Q_\text{out} = -Q_\text{in}$
در پاسخ Kostya فرض شده است که $Q_\text{out}$ باید مثبت باشد، به همین دلیل است که او نتیجه می گیرد که موتوری با این کارایی نمی تواند وجود داشته باشد. اما من می خواهم با در نظر گرفتن ارزش اسمی آن رویکرد متفاوتی داشته باشم: کارآمدترین موتور در این شرایط موتوری است که در واقع گرما را از مخزن سرد خارج می کند:

یک موتور حرارتی فوق کارآمد که با یک مخزن دمای منفی کار می کند. توجه داشته باشید که گرما را از هر دو مخزن خارج می کند.
اکنون می توانیم مقدار مشخصی از بازدهی بیشتر از یک را احساس کنیم. اگر$\eta>1$ به این معنی است که W بزرگتر از Qin است. اما این مشکلی ندارد زیرا در این شرایط بخشی از انرژی از مخزن سرد می آید. با قانون دوم مشکلی وجود ندارد، زیرا ما این را با تنظیم صریح افزایش آنتروپی روی 0 به دست آوردیم.
من می خواهم به عقب برگردم و چیزی را که قبلاً به آن اشاره کردم روشن کنم: می توانید گرما را از یک مخزن با دمای منفی خارج کنید و برخلاف گفته کلوین مستقیماً آن را به کار تبدیل کنید. یعنی این موتور امکان پذیر است:

یک موتور حرارتی که گرمای دمای منفی را مستقیماً به کار تبدیل می کند.
اما این منافاتی با قانون دوم ندارد. موتور فوق حداکثر کارایی را ندارد و مقدار آنتروپی$-\frac{1}{T}Q$ تولید می کند که باز هم مثبت است زیرا T منفی است.
شما نمی توانید از آن برای ساخت یک ماشین حرکت دائمی استفاده کنید، زیرا دمای مخزن دمای منفی با حذف گرما از آن کاهش می یابد، تا زمانی که دمای آن به منهای بی نهایت برسد (که در زمان محدود انجام می دهد)، در این مرحله آن را انجام می دهد. به مثبت بودن تغییر خواهد کرد و به کاهش ادامه خواهد داد. این احتمالاً کاملاً غیرمعمول به نظر می رسد، بنابراین بخش مربوط به آن را در زیر ببینید.
بنابراین نتیجه همه اینها این است که بله، ممکن است η بزرگتر از 1 باشد اگر TH<0 باشد، اما این یک مثال متضاد با قانون دوم نیست و اجازه ساخت یک موبایل دائمی را نمی دهد. بیانیه کلوین قبل از آگاهی از دماهای منفی نوشته شده است، همانطور که شما می گویید، و برای اینکه برای چنین سیستم هایی صادق باشد، باید به گونه ای اصلاح شود که "هیچ فرآیندی ممکن نیست که تنها نتیجه آن جذب گرما از یک مخزن با مثبت باشد. دما و تبدیل کامل آن به کار."
چرا دما به -∞ کاهش می یابد و سپس مثبت می شود؟
در نپاسخ قبلی این پاسخ گفتم که برای ایجاد یک مخزن دمای منفی نیاز به کار دارید. این تا حدی درست است، اما من فکر میکنم استدلال زیر بهتر است.
با ذکر این نکته شروع می کنیم
$\frac{1}{T} = \frac{\partial S}{\partial U},$
که در آن U انرژی داخلی یک سیستم و S آنتروپی آن است. برای اکثر سیستم ها منحنی S(U) چیزی شبیه به این است:

: منحنی S(U) برای یک جسم معمولی با ظرفیت حرارتی محدود.
می بینید که با حذف گرما از سیستم (کاهش U)، شیب$1/T$ افزایش می یابد (یعنی T کاهش می یابد) تا زمانی که در نقطه ای با U محدود (انرژی حالت پایه)، آنتروپی صفر و شیب بینهایت می شود. (یا T صفر می شود). این یک نتیجه اساسی از مکانیک آماری است که منحنی S(U) باید مقعر باشد، به این معنی که $1/T$ همیشه باید با افزایش U. Ty افزایشی نداشته باشد.
از نظر ظاهری، S و U هر دو نامحدود هستند.
با این حال، برای برخی از سیستمها (آنهایی که میتوانید وارونگی جمعیت داشته باشید) فقط میتوانند مقدار محدودی انرژی در خود نگه دارند، و برای آن سیستمها منحنی بیشتر شبیه این است:
 منحنی S(U) برای سیستمی که می تواند دمای منفی داشته باشد.
منحنی S(U) برای سیستمی که می تواند دمای منفی داشته باشد.می بینید که این سیستم ها می توانند دماهای منفی داشته باشند، به این معنی که انرژی داخلی U در سمت راست پیک در S است. با حذف گرما از چنین سیستمی، $1/T$ افزایش می یابد تا زمانی که از صفر عبور کند و دوباره مثبت شود. که مربوط به کاهش -∞ T است، سپس به +∞ تغییر می کند و به کاهش ادامه می دهد.
بنابراین همانطور که انرژی را از یک مخزن با دمای منفی حذف می کنید، به ناچار آن را به یک مخزن با دمای مثبت طبیعی نزدیک می کنید. این دلیل اساسی است که چرا نمیتوانید یک ماشین حرکت دائمی با استفاده از مخازن دمای منفی بسازید: در نهایت ایدهآلسازی دمای ثابت باید از بین برود و مخزن دمای منفی شما به یک مخزن دمای مثبت تبدیل شود.
برعکس، برای ایجاد مخزن دمای منفی در وهله اول، باید انرژی را در آن صرف کنید. یک سیستم با منحنی S(U) که در شکل 4 نشان داده شده است، معمولاً در همان دمای (مثبت) محیط اطراف خود شروع می شود، به این معنی که انرژی داخلی U آن در سمت چپ قله در منحنی S خواهد بود. برای منفی کردن دما، باید با استفاده از یک پمپ حرارتی (مشابه شکل 2 اما با تمام فلش ها در جهت مخالف) در آن انرژی قرار دهید. در اصل، شما باید آن را آنقدر گرم کنید که دمای آن بی نهایت و سپس منفی شود. بنابراین اگرچه ممکن است کاملاً معجزهآسا به نظر برسد که گرمای دمای منفی میتواند 100% بدون تولید گرما به کار تبدیل شود، باید در نظر داشته باشید که سیستمهای دمای منفی چیز بسیار خاصی هستند که (تا آنجا که من میدانم) وجود ندارند. در طبیعت، و شما نمی توانید بدون استفاده از حداقل کاری که می توانید با استفاده از یک موتور حرارتی از آن استخراج کنید، یکی بسازید.
آیا گرما نباید از مخزن دمای منفی H به مخزن دمای مثبت C جریان یابد؟
اگر از موتور حرارتی برای استخراج کار استفاده نمی کردیم، بله، این کار را می کرد. همانطور که امیدواریم به وضوح از شکل 5 بالا مشاهده کنید، دمای منفی گرمتر از دمای مثبت است. اما نکته این است که ما فقط یک جریان خود به خودی گرما را در نظر نمی گیریم، بلکه کارآمدترین راه را برای استخراج کار از مخازن با استفاده از یک ماشین فرضی در نظر می گیریم.
ممکن است نگاهی دوباره به شکل 1 که یک موتور حرارتی معمولی را نشان می دهد کمک کند. در اینجا ما گرمایی داریم که از یک مخزن گرم خارج می شود و به مخزن سرد می رود. اما گرمایی که وارد مخزن سرد می شود کمتر از گرمای خارج شده از مخزن گرم است، زیرا مقداری از آن به کار تبدیل می شود. اگر TH را در حالی که Qin ثابت نگه داریم، افزایش دهیم، موتور می تواند کارآمدتر عمل کند، بنابراین $Q_\text{out}$ کاهش می یابد. اگر TH را بینهایت کنیم (یعنی $1/T_H=0$، بنابراین مخزن داغ درست در اوج منحنی S(U) در بالا قرار دارد) آنگاه $Q_\text{out}$ صفر می شود، زیرا موتور حرارتی با حداکثر کارآمدی بازده 1 دارد و می تواند گرما را در آن تبدیل کند. $T_\infty$ بدون تولید گرما کار کند. (به یک معنا، کار گرما با دمای بی نهایت است.)
اگر انرژی مخزن داغ را بیش از این افزایش دهیم، به طوری که دمای آن منفی شود (گذر از پیک روی منحنی S(U))، حداکثر بازده ممکن بیشتر از 1 و$Q_\text{out}$ منفی می شود. توجه داشته باشید که در این حالت موتور حرارتی گرما را از هر دو مخزن خارج می کند..I hope I have helped you in understanding the question. Roham Hesami, seventh semester
aerospace engineering



