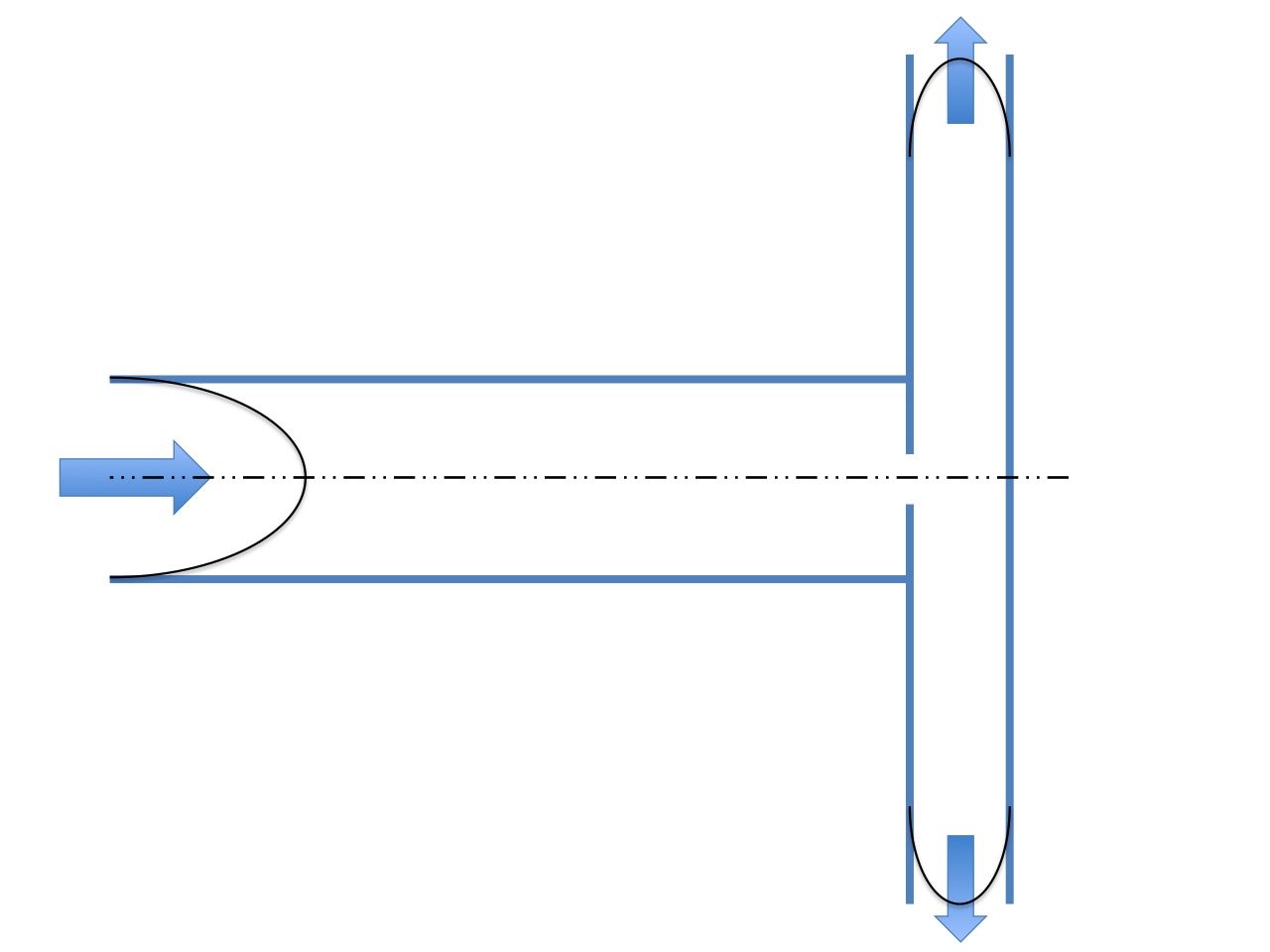
روش کلی برای حل مشکلات جریان سیال
آیا کسی می تواند به من کمک کند تا یک سری مراحل کوتاه را برای حل مشکل جریان سیال دلخواه طراحی کنم؟ اغلب سختترین بخش این مشکلات این است که بفهمم چه مسیری را برای حل آنها باید طی کنم و من سعی میکنم بهترین روش کلی را برای آمادگی برای امتحان نهایی در ذهن خود جمع کنم.
برای مثالی عینی از منظورم: برای قیاس با فیزیک کلاسیک، روش کلی این است که
شناسایی نیروها (نیروهای جسم، نیروهای تماسی، نیروهای عادی)
سیستم را به اجزای بعدی تقسیم کنید
سیستم معادلات حاصل را حل کنید. این برای "اکثر" سیستم ها کار می کند.
من به دنبال یک روش مشابه جریان سیال هستم. این بهترین تلاش من است:
معادلات ناویر استوکس را برای مختصات دکارتی، استوانه ای یا کروی بنویسید. این به شما تعادل حرکتی می دهد.
تمام عبارات را بر اساس فرضیات خط بزنید (به عنوان مثال، ویسکوزیته را در صورتی که جریان نامرغوب است، خط بکشید. اگر جریان متقارن در یک استوانه باشد، عبارات زاویه ای را خط بزنید، و غیره)
معادله تداوم را بنویسید. این به شما تعادل جرم می دهد، بنابراین اکنون باید از جرم و حرکت مراقبت کنید.
معادله ای را بنویسید که مجهولات بیشتری را به خواص ماده مربوط می کند.
آیا پیشنهادی برای اصلاح یا توضیح دارید؟ من چیزی در مورد لایه های مرزی یا لایه های مرزی حرارتی یا جریان آشفته / آرام و غیره در آنجا گنجانده ام.
مقادیر مربوط به سیستم خود را شناسایی کنید: انرژی، تکانه، آنتروپی، بار الکتریکی، جرم ...
که ممکن است حفظ شود یا نباشد. اگر شرایط مرزی دارید، به احتمال زیاد صرفهجویی در انرژی و/یا تکانه در سیستم ندارید. در هر صورت، شما باید معادلات پیوستگی را برای مقادیر سیستم خود بنویسید، که ممکن است اصطلاحات منبعی داشته باشند که به دلیل این عدم حفاظت باشد.
بنابراین، اگر به یک سیال غیر نسبیتی، عاری از مرز، بدون هزینه ذخیره اضافی فکر کنید.
متغیرهای مربوطه عبارتند از: سرعت (در اصل به خوبی تعریف شده) $\vec v$، چگالی جرم $ρ$، تانسور تنش$ σ،$ که برهمکنش درون سیال را نشان میدهد، و همچنین چگالی نیروی خارجی که بر روی سیال اثر میکند،$\vec f$.
بر اساس این قوانین کلی برای سیستم خود معادلات کلی بنویسید. ناویر استوکس از بقای تکانه، با انتخاب خاصی برای تانسور تنش حاصل می شود.
بنابراین، یک مثال از معادلات در این مورد، قرار دادن یک سیال غیر نسبیتی بدون مرز است،
$\frac{\partial \rho}{\partial t}+\nabla \cdot \left(\rho \vec v\right)=0$
$\frac{\partial}{\partial t}\left(\rho \vec v\right)+\nabla \cdot \left(\rho \vec v\otimes \vec v + \sigma\right)=\vec f$
بنابراین شما با 2 معادله پیوستگی مواجه می شوید، اولین معادله بدون منبع، که بقای جرم سیال را توصیف می کند. دومی که بقای تکانه سیال را توصیف می کند، در اصل یک اصطلاح منبع دارد، یعنی چگالی نیروی خارجی (به گرانش فکر کنید).
شما هنوز به یک معادله برای بقای انرژی و آنتروپی نیاز دارید.
اینجا همچنین جایی است که باید شرایط مرزی و مرتب سازی را در آن لحاظ کنید. میتوانید f⃗ را وارد کنید (حداقل به صورت عددی، مانند روشهای ذرهای)، یا معادلات محدودی بنویسید، که میتواند برای مثال، سرعت نسبی صفر در نزدیکی دیواری با سیال چسبناک، یا انرژی محدود و سیستم تکانه بدون آزاد باشد. مرزها
معادلات تشکیل دهنده را بنویسید. من معتقدم این مشکل ترین بخش است، زیرا نمی توان شکل کلی آنها را تنها از اصول تقارن استنتاج کرد. اینجا جایی است که باید معادله حالت (EoS) را برای سیستم وارد کنید و همچنین در صورت وجود باید افکتهای حافظه را نیز درج کنید.
در اینجا، اگر در حال مطالعه سیالات نیوتنی هستید، شکل زیر از تانسور تنش را دارید:
$\sigma_{ij} = p\delta_{ij}- \eta\left(\frac{\partial v_i}{\partial x_j} + \frac{\partial v_j}{\partial x_i}\right) - \delta_{ij} (\zeta-\frac{2}{3}\eta) \nabla \cdot \mathbf{v}$
جایی که شما اکنون به یک معادله حالت برای η و ζ و p نیاز دارید، اما در اصل، آنها توابعی از ρ و T (دما) هستند، اما تمام. هنگامی که به اینجا رسیدید، باید یک توصیف هیدرودینامیکی "کامل" از سیستم خود داشته باشید.
مسئله خود را به صورت عددی فرموله کنید: مسئله خود را گسسته کنید، معادلات تقریبی را بنویسید، یا با استفاده از روش های مش پر (تفاوت های محدود، اجزای محدود...) یا بدون مش (هیدرودینامیک ذرات صاف...) و پیاده سازی بر روی کامپیوتر با استفاده از زبان برنامه نویسی مورد علاقه شما
بسیاری از پیشرفتها در دیدگاه عملی به جای تلاش برای حل «با دست» به این روش انجام میشود
'. این موضوع در مورد سیالات غیر نیوتنی اهمیت بیشتری دارد.
هنوز مهم است که رویکردهای جایگزین برای موارد خاص را فراموش نکنید. اولین مثالی که به ذهن من می رسد نظریه آماری آشفتگی است (نظریه K41 و مواردی که به دنبال آن هستند). حتی اگر تمام اطلاعاتی را که برای به دست آوردن وجود دارد به دست نمی آورید، می توانید به صورت پدیدار شناختی به مسئله حمله کنید، که در بسیاری از موارد بیشتر از چیزی است که اگر مستقیماً به مشکل حمله کنید، به دست می آورید.
در آخر:
من چیزی در مورد لایه های مرزی یا لایه های مرزی حرارتی یا جریان آشفته / آرام و غیره در آنجا گنجانده ام. بهترین نقطه برای بیان این ملاحظات چیست؟
من معتقدم که آنها در بخش 2 قرار می گیرند، زیرا در مورد تلاطم، شما معمولاً با جریان آرام رفتار می کنید، بنابراین نیاز به مجموعه ای متفاوت از معادلات است. در نتیجه شما باید 1 و 3 را نیز تطبیق دهید، اما، به نظر من، نقطه اصلی در 2 است.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering


رهام حسامی ترم ششم مهندسی هوافضا