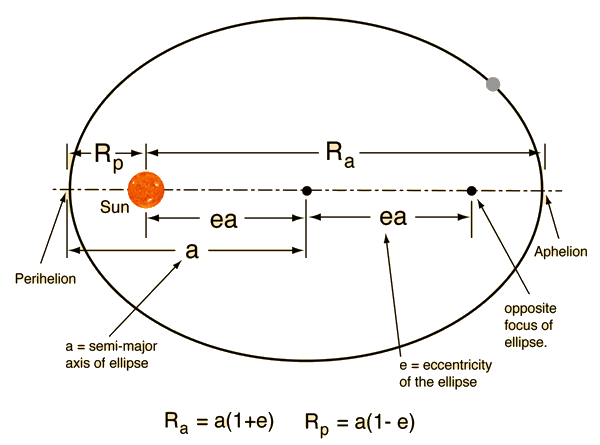
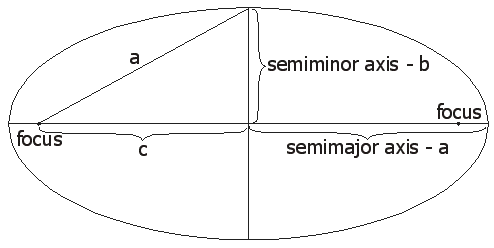
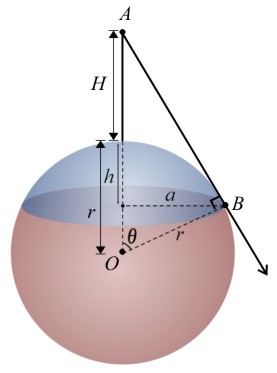
(پاسخ: e = 1.581)
چگونه می توان این مشکل را بدون دانستن اینکه ماهواره به دور چه جسمی در حال چرخش است یا زاویه مسیر پرواز یا ویژگی های دیگر را حل می کند؟
یافتن یک سیاره و ارتفاع نمونه (μ) که برای آن یک مدار دایره ای ساده است، آسان است. اگر فرض کنید که یک مدار دایره ای است، پس
$a_c=v^2/r=\mu/r^2$
$\mu=v^2r=(45000 ft/s)^2*(4,000 n mi)=4.92*10^{15} ft^3/s^2$این باعث می شود فکر کنم این باید در اطراف زمین باشد، اما این به وضوح در مشکل بیان نشده است.
اما حتی از آنجا، شما زاویه پرواز مدار در 90 درجه را نمی دانید که به ما اجازه نمی دهد سرعت زاویه ای مدار را پیدا کنیم. دانستن پاسخ 1.581 است، ما می دانیم که این یک مدار هذلولی است و یا باید سیاره را ترک کند یا فقط برای خروج به سیاره بیاید، اما نمی دانیم از چه زاویه ای. ممکن است تقریباً مستقیماً روی زمین بیاید.
شما باید فرض کنید که با زمین کار می کنید، در حالی که در مشکل ذکر نشده است.
شما با محاسبه انرژی ویژه (ε) مدار با توجه به سرعت های زیر شروع می کنید:
$\epsilon=\frac{V^2}{2}-\frac{\mu}{r}$از آنجا شما محور نیمه اصلی (a) مدار را محاسبه می کنید:
$\epsilon = -\frac{\mu}{2a} \therefore a = -\frac{\mu}{2\epsilon}$
بعد، پارامتر (p) مدار را پیدا می کنید:
$r = \frac{p}{1+e\cos{v}}=\frac{p}{1+e\cos{90°}} = p$
در نهایت، می توانید همه آن را با هم در یک معادله از تعریف یک بخش مخروطی قرار دهید:
$p = a(1-e^2) \therefore e = \sqrt{1-\frac{p}{a}}$Hesami, sixth
semester of aerospace engineering