$V_3 = \sqrt{2g\left(\frac{P_1}{\rho g}+ z_1-\Delta h_L\right)}$
که در آن$\Delta h_L$) افت کل سر در لوله ها است.
سوال من این است که اگر سیستم را طوری تغییر دهم که اکنون چهار نازل در یک پیکربندی موازی وجود دارد سرعت نازل جدید چقدر است؟ آیا معادله سرعت نازل ثابت می ماند (البته با افت سر متفاوت)؟ یا اینکه به جای آن تداوم اعمال می شود، در این صورت سوال من این است که چگونه می توانم نرخ جریان را از طریق نقطه شماره تعیین کنم. 2؟
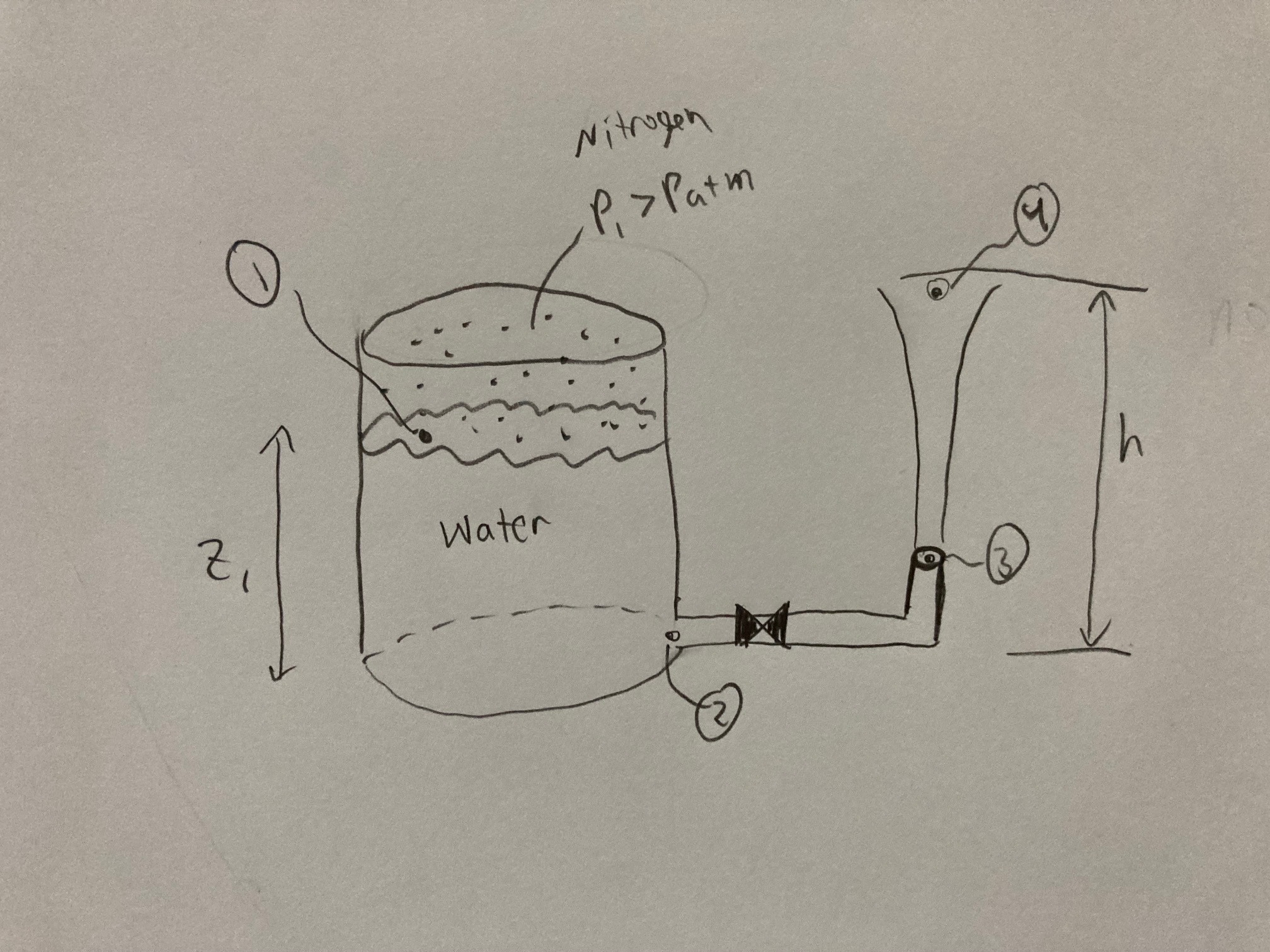
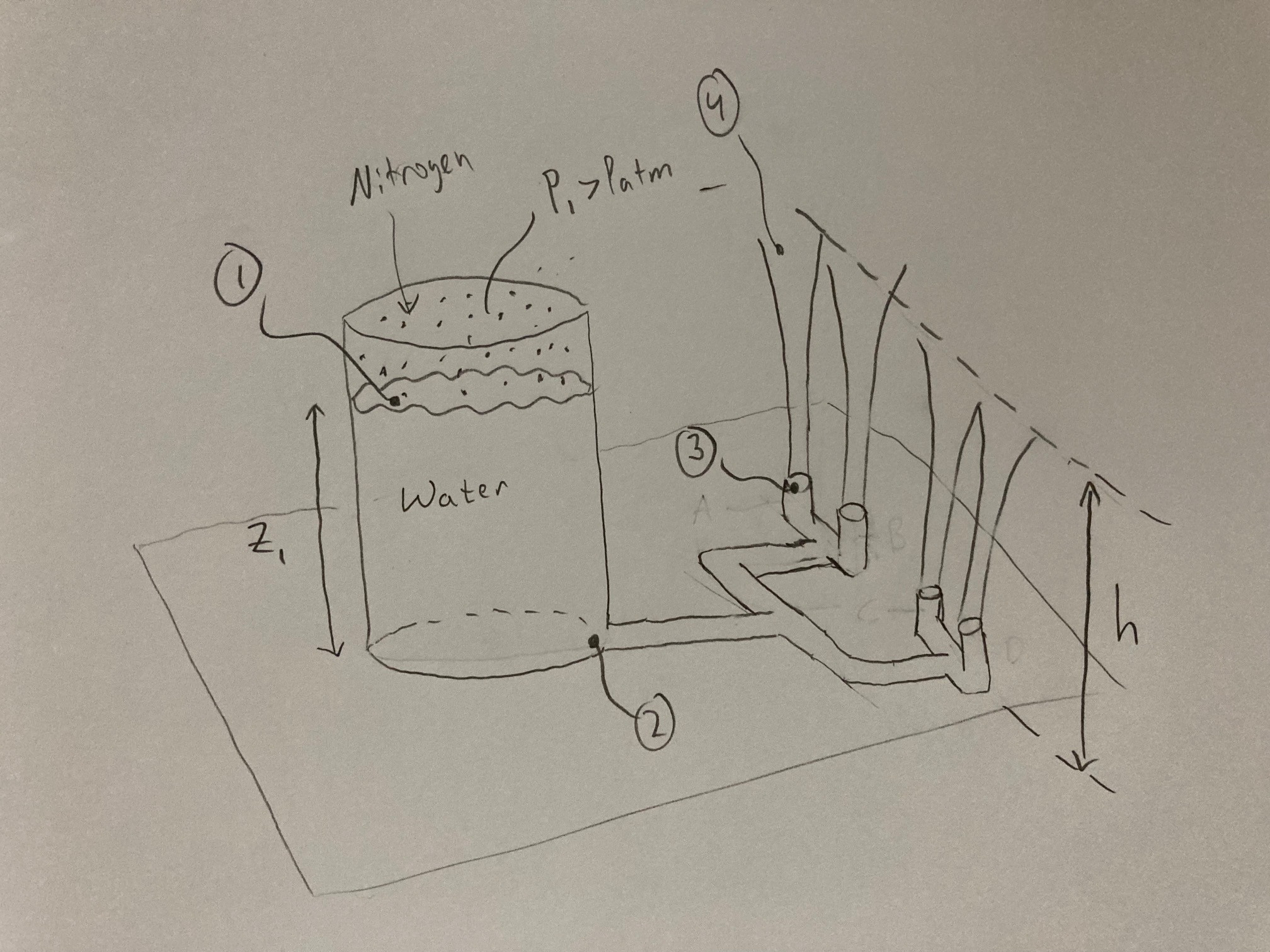
بدون تلفات هد، وقتی $A_2 > A_3$ سرعت جریان از نقطه 2 در مورد 2 (با چهار لوله در خروجی) بیشتر از حالت 1 خواهد بود. از آنجایی که ما هیچ اطلاعاتی در مورد تلفات هد نداریم، در زیر نحوه مقایسه نرخ جریان در شرایط ایده آل را نشان می دهم. توجه داشته باشید که $A_3$ سطح مقطع کل هر چهار لوله را در نقطه 3 در مورد 2 نشان می دهد.
یا به جای آن تداوم اعمال می شود
معادله پیوستگی زمانی اعمال میشود که جرم یک سیال متحرک با جریان آن تغییر نمیکند، که در مثال شما چنین است: حجم (جرم) که از چهار لوله خارج میشود برابر است با کاهش حجم (جرم) در مخزن.
$A_1 v_1 = A_2 v_2 = A_3 v_3$
که در آن q دبی حجمی، A سطح مقطع، و v سرعت سیال است. توجه داشته باشید که در اینجا $A_3$ به معنای سطح مقطع ترکیبی هر چهار لوله است. با ترکیب معادله تداوم و ایده آل سازی معادله برنولی
$p + \rho g y + \frac{1}{2} \rho v^2 = \text{const.}$
ساده است که نشان دهیم نسبت سرعت برای این دو مورد برابر است
$\frac{v_2'}{v_2} = \sqrt{\frac{(A_1/A_2)^2 - 1}{(A_1/A_3)^2 - 1}} \qquad \text{and} \qquad \frac{v_3'}{v_2} = \sqrt{\frac{1-(A_2/A_1)^2}{1-(A_3/A_1)^2}}$
که در آن $v_2'$ و $v_3'$سرعت در نقطه 2 و 3 در مورد 2 و $v_2$سرعت در نقطه 2 در مورد 1 است.
آیا معادله سرعت نازل ثابت می ماند (البته با افت سر متفاوت)؟
بدون افت سر و با فرض $A_1 > A_2$ و$A_1 > A_3$، اکنون مشخص است که$v_2' > v_2$ و $v_3' > v_3$ زمانی که $A_3 > A_2$و بالعکس.
این را نیز می توان به طور مستقیم حل کرد:
وقتی $A_3 = A_2$، که در آن A3 سطح مقطع چهار نازل ترکیب شده است، نقطه 1 همان مقطع را به خروجی در فشار اتمسفر می بیند. بنابراین، سرعت خروجی در نقاط 2 و 3 در مورد 2 در مقایسه با نقطه 2 در مورد 1 یکسان باقی می ماند.
همانطور که A3 با شروع از$A_3 = A_2$ کوچکتر می شود، نقطه 1 سطح مقطع خروجی کوچکتری می بیند و سرعت در نقطه 3 کاهش می یابد. در شدیدترین حالت، وقتی A3=0 سرعت صفر است. با کاهش سرعت در نقطه 3، سرعت عبور از نقطه 2 نیز کاهش می یابد.
همانطور که A3 با شروع از $A_3 = A_2$بزرگتر می شود، نقطه 1 سطح مقطع خروجی بزرگتر را می بیند و سرعت در نقطه 3 افزایش می یابد. با افزایش سرعت در نقطه 3، سرعت عبور از نقطه 2 نیز افزایش می یابد.hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering



