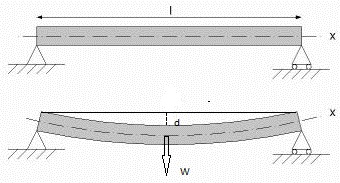
$d = \frac {Wl^2}{4Ybt^3}$
جایی که Y مدول یانگ تیر است و l,b,t به ترتیب طول، عرض و ضخامت تیر است.
علاوه بر این، اگر از استوانهای با شعاع r و ارتفاع/طول l استفاده میشد، فرمول به این صورت میشد:
$d = \frac {Wl^2}{12Yπr^4}$
فرمول ها صحیح هستند و موارد خاصی از انحراف مرکزی یک تیر ساده با بارگذاری مرکزی است که
$\delta=\frac{Wl^2}{48YI}$
در نامگذاری شما (اما به جای d با δ). در اینجا، I لحظه دوم مساحت یا ممان مساحت اینرسی است، که معیاری است برای اینکه مناطق مقطع پرتو چقدر از مرکز فاصله دارند. به طور شهودی، هرچه سطح مقطع بیشتر باشد، خم کردن تیر سختتر میشود.
این معادله به نوبه خود یک مورد خاص از حل معادله انحراف تیر اویلر-برنولی است که
$\frac{d^2}{dx^2}\left(YI\frac{d^2\delta(x)}{dx^2}\right)=q(x)$
جایی که من دوباره از δ استفاده می کنم تا از اشتباه گرفتن با عملگر دیفرانسیل جلوگیری کنم و q(x) نیروی توزیع شده روی میله است. (در مورد شما، این نیروی توزیع شده در یک توده به مرکز میله می رسد.)
استخراج این معادله کلی و حل آن بخشی از محتوای یک دوره دانشگاهی مهندسی است. این شامل یک نمودار بدن آزاد از بخش کوچکی از تیر و یک موازنه نیرو برای بیان انحنای آن بخش کوچک بر حسب توزیع نیرو در هر دو انتها و در طول آن است. موازنه نیرو به یک انتگرال در سراسر مقطع نیاز دارد (برای تطبیق نیروهای فشاری در نیمه بالایی و نیروهای کششی در نیمه پایینی)، که من از آنجا آمده ام. همچنین قانون هوک، σ=Yε را برای تبدیل تغییر شکل ها به نیرو و بالعکس، در خود جای داده است. علاوه بر این، بر این فرض تکیه دارد که انحنا$\rho\approx(d^2\delta(x)/dx^2)^{-1}$و مجموعه ای از مفروضات دیگر
..hope I helped you understand the question. Roham Hesami, sixth semester of aerospace engineering



