مطابق با شکل زیر مخزنی استوانهای را در نظر بگیرید. فرض کنید این مخزن حاوی گازی با فشار p است. مطابق با شکل زیر قطر و ضخامت این مخزن به ترتیب برابر با D و t و طول آن برابر با L در نظر گرفته شدهاند. برای بدست آوردن تنش مماسی، مخزن مطابق با شکل زیر برش زده میشود
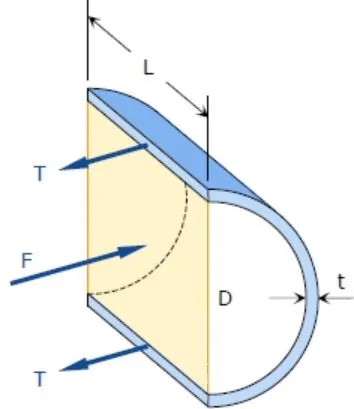
پوسته آبی رنگ در تعادل است؛ بنابراین نیروی ناشی از فشارِ p با نیروی ناشی از تنش مماسی برابر است. در نتیجه با نوشتن رابطه تعادل داریم:
$\Large 2 T = F$
از طرفی نیروی T برابر با حاصل ضرب تنشِ σt در مساحتِ tL است. بنابراین رابطه فوق را میتوان به صورت زیر بازنویسی کرد.
$\Large 2 ( \sigma _ t t L ) = p D L$
نهایتا تنش مماسی در یک مخزن جدار نازکِ استوانهای با فشار p برابر با مقدار زیر بدست میآید.
$\Large 2 t \sigma _ t = p D$
رابطه ۱$\Large \boxed {\sigma_t = \dfrac { p D } { 2 t } }$
برای بدست آوردن تنش طولی کافی است تا مخزن استوانهای مطابق با شکل زیر، به صورت عمود به طول استوانه برش زده شود.
تنش در مخازن
نیروی وارد به انتهای استوانه برابر است با:$\Large F = p A = p \dfrac { \pi} {4} D ^2$
از طرفی تنش طولی تنها روی بخش جدار نازک اعمال میشود. مساحت این قسمت برابر با
$\large A = \pi D t$
است. از این رو نیروی ناشی از تنش طولی نیز برابر است با:
$\Large P _ T = \sigma _ L \pi D t$
در مرحله بعد معادله تعادل نیرویی را به صورت زیر بیان میکنیم.
$\Large \Sigma F _ H = 0$و$\Large P_T = F$و$\Large \sigma _ L \, \pi D t = p \dfrac {\pi} { 4 } D ^ 2$
نهایتا تنش طولی به صورت زیر بدست میآید.
$\Large \boxed {\sigma_t = \dfrac { p D } { 2 t } }$
توجه داشته باشید در روابط فوق منظور از فشار، در حقیقت اختلاف فشار داخل و بیرونِ مخزن است. بنابراین با فرض این که فشار داخلی برابر با pi و فشار خارجی برابر با po باشد، رابطه زیر را میتوان برای تنش طولی بیان کرد.$\Large F = p A = p \dfrac { \pi} {4} D ^2$
با توجه به روابط ۱ و ۲، رابطه زیر را میتوان بین تنشهای افقی و عمودی نوشت.
$\Large \sigma _ t = 2 \sigma _ L$
تنش در مخازن کروی
به دلیل متقارن بودن شکل کره نسبت به تمامی محورهایی که از مرکز آن عبور میکنند، تنش در پوسته یک مخزن کروی، در تمامی جهات با هم برابر هستند. از این رو به منظور محاسبه تنش، تنها کافی است تا مطابق با شکل زیر، کره را در جهتی دلخواه برش بزنید.
تنش در مخازن
نیروی داخلیِ ناشی از فشار که به نیمکره وارد میشود، برابر است با:
$\Large P = p ( \frac { 1 } { 4 } \pi D ^ 2 )$
این نیرو برابر با تنشی است که به جداره وارد میشود. بنابراین میتوان گفت:
$\Large P_T = F$
$\Large \sigma \pi D t = p (\frac {1}{4} \pi D ^ 2)$
نهایتا تنش در جداره یک مخزن کروی با فشار p برابر است با:
$\Large \boxed { \sigma = \dfrac { p D } { 4 t } }$
نحوه محاسبه مقاومت فشار خارجی سیلندرها و کره ها
اگر دیواره های مخزن به اندازه کافی نازک باشد، تحت فشار خارجی نه به دلیل رسیدن مواد به نقطه تسلیم، بلکه به دلیل ناپایداری (کمانش) از بین می رود. به عنوان مثال، یک فشار بحرانی برای یک استوانه بی نهایت جدار نازک با شکل کامل $p=\frac{2 E}{1-\mu^2}(t/D)^3$ است، که در آن E مدول الاستیسیته، μ نسبت پواسون، t ضخامت دیواره و D قطر سیلندر است
حداقل ضخامت یک مخزن تحت فشار سیلندر بیضویبرای مخازن تحت فشار به شکل استوانههای دایرهای، میتوانیم از σhoop=prt استفاده کنیم تا حداقل ضخامت پوست را با تنظیم تنش حلقه حداکثر مقدار مجاز و سپس حل کردن t استفاده کنیم. اما، سیلندرهای بیضوی (پیچیده تر) چطور؟
از آنجایی که بیضی ها دارای یک محور نیمه اصلی و یک محور نیمه فرعی هستند (برخلاف دایره هایی که فقط یک شعاع دارند)، منطقی است که یک مخزن تحت فشار استوانه ای بیضی دارای دو حداقل ضخامت (به جای تنها یک) باشد. آیا این درست است؟ اگر چنین است، چگونه می توان آنها را پیدا کرد؟
اگرچه یکسان نیستند، اما معمولاً میتوانند ناحیه موجود را در مقایسه با رگهای بیضوی (برای یک بعد معین A و B) بهینه کنند. به این ترتیب، اینها تقریباً همیشه انتخاب ترجیحی طراحی در مقایسه با بیضوی هستند و بیشتر به صورت تجاری در دسترس هستند. معادلات، در حالی که ناپیوستگی تنش غشایی را مدیریت می کنند، آسان تر هستند.
اساس فرض دیوار نازک
ما به راحتی می توانیم یک نسخه دیوار نازک از این را استخراج کنیم. می توان توجه داشت که بیضی نشان داده شده در بالا را می توان به صورت تمام نقاط بیان کرد
$(\frac{b}{2}\cos(\phi),\frac{a}{2}\sin(\phi))$
با پارامتر φ که از 0 تا $2\pi$ متغیر است. توجه داشته باشید که این همان زاویه از مرکز، θ نیست، اما با رابطه با این زاویه مرتبط است
$\tan(\theta) = \frac{b}{a} \tan(\phi)$
برای یک ϕ داده شده، تنش در یک ظرف جدار نازک به راحتی قابل مشاهده است. مشابه یک ظرف دایره ای، یک مقطع را به نقطه ای در ϕ مشخص تا مرکز می بریم. با استفاده از تقریب دیواره نازک مشابه مانند رگ های استوانه ای، فرض می کنیم تنش مماسی (غشاء) در سراسر این برش با ضخامت t یکنواخت است. ما فرض می کنیم که بدون توجه به ϕ به عنوان$t<<a ; t<<b$یکنواخت است. فاصله D(φ) تابعی است بر اساس ϕ از لبه، از طریق مرکز تا لبه دیگر به راحتی قابل انجام است.
$D(\phi) = \sqrt{b^2\cos^2(\phi) + a^2\sin^2(\phi)}$
. از آنجایی که دیوار به طور یکنواخت روی این برش با فشار P فشار داده می شود، پس واضح است که، مشابه دایره ها، برای بار در واحد طول بر اساس:
$PD(\phi) = 2t\sigma(\phi)$
$\sigma_t(\phi) = \frac{PD(\phi)}{2t}$.
با فرض ثابت بودن محیط
توجه داشته باشید که غلظت تنش قطعا ظاهر می شود، زیرا کشتی می خواهد شکل استوانه ای به خود بگیرد. با اجرای یک برش از هر دو محور x و y و اجرای یک تحلیل استاتیکی این بخش، متوجه میشویم که تنش مماسی بسیار کوچکتری از یک محور نسبت به دیگری ایجاد میشود. کرنش غیر یکنواخت مطمئناً باعث ایجاد گشتاورهای خمشی در مواد جدار نازک می شود.
بدون اجرای تجزیه و تحلیل دیواره ضخیم، این غلظت تنش را نمی توان دقیقاً تعیین کرد. برای این فرض دیوار نازک، ما به سادگی فرض می کنیم که محیط قبل و بعد از انحراف تقریباً یکسان می ماند. محیط یک بیضی با استفاده از انتگرال های بیضوی تعیین می شود. تعریف:
$k^2 = 1-\frac{a^2}{b^2}$
سپس محیط بیضی 2bE(k)$$ است، جایی که E انتگرال بیضی نوع دوم است. توجه می کنیم که k تابعی از b است. با گرفتن مشتق از این با توجه به b، و ریاضیات زیاد، به این نتیجه زیبا می رسیم که:$\frac{E(k)}{F(k)} = \frac{a^2}{b^2}$
ما E(k) و F(k)، انتگرال بیضوی نوع اول را به عنوان یک ثابت برای تغییرات کوچک در k ناشی از تغییرات a و b تقریب میکنیم. به این ترتیب، برای یک انقباض کوچک b، Δb، انبساط a، Δa را به صورت زیر مییابیم:
$\Delta a = - \frac{b^3}{a^3} \Delta b$
رابطه مکعبی نشان می دهد که بیضی های بسیار غیرعادی به سرعت از شکل بیضی به شکل استوانه ای تبدیل می شوند! به این ترتیب، تقریب های فوق به سرعت نامعتبر می شوند. منفی دلالت بر انبساط در مقابل انقباض است. با این اطلاعات، میتوان تلاش کرد تا غلظت تنش را به یک تقریب معقول حل کنیم. تنش "شعاعی" از نمای ایستا نشان می دهد که باید رشد شعاعی خطی داشته باشد، در حالی که تحلیل محیطی رشد شعاعی مکعبی را نشان می دهد. این انحراف خود را به عنوان یک نیرو نشان می دهد و غلظت خمشی را در نوک لبه b (بدترین حالت) تقریباً اضافه می کند:$M = \frac{Pb^2(b^2-a^2)}{4a^2}$
$\sigma_b = \frac{3Pb^2(b^2-a^2)}{2t^2a^2}$
این تنش باید b با محور دیگر جایگزین شود تا دو تنش حداکثر در رگ بدست آید. توجه داشته باشید که تنش مماسی اصلی باید به تنش خمشی اضافه شود. به این ترتیب، کل تنش در سمت محور طولانی خواهد بود:$\sigma_b = \frac{3Pb^2(b^2-a^2)}{2t^2a^2} + \frac{Pb}{2t}$
با جمع کردن تنش محوری تجزیه و تحلیل مورد به مورد خود (پیچیده است، اما می توان با تقسیم مساحت یک کلاهک بیضی بر محیط عجیب بیضی منطقی فرض کرد)، و تنش های یک Von- را دارید. استرس را از دست می دهد. این، به عنوان تابعی از ضخامت، روی حداکثر مقدار تنظیم می شود، و حداقل ضخامت نتیجه ای است که به تنش اجازه می دهد تا به حداکثر مقدار برسد. این بخش معمولاً در طراحی مخازن تحت فشار استفاده می شود، زیرا بارگذاری محیطی بیش از آنچه معادله شما فرض می کند، تنش می افزاید.$ \underbrace{-\nabla p - \rho\nabla \varphi = 0}_\textrm{equation of hydrostatics}\,.\tag{I}$
hope I helped you understand the question. Roham Hesami, sixth semester of aerospace engineering



