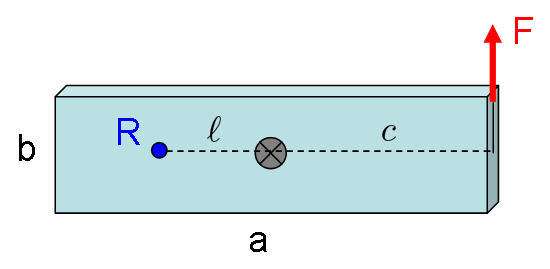
منظور از شعاع ژیراسیونRadius of gyration چیه شعاع چرخش اسم. طولی که نشاندهنده فاصله یک سیستم دوار بین نقطهای که در اطراف آن میچرخه و نقطهای که انتقال انرژی به آن یا از آن بیشترین تأثیر را دارد، است. نماد: k یا r. در سیستمی با ممان اینرسی I و جرم m، k ² = I / m.نکته شعاع چرخش یک ویژگی هندسی یک جسم صلب مانند مرکز جرم است. اگر میخواهید یک جسم مسطح را با یک حلقه دایرهای نازک به شعاع r جایگزین کنید، اگر میخواهید که حلقه پاسخ دینامیکی مشابه جسم صلب شما داشته باشد، $I=m r^2$را انتخاب میکنید.علاوه بر این، می توانید از آن برای پیدا کردن فاصله ℓ مرکز کوبه از یک محور استفاده کنید.
$\boxed{ \ell = c + \dfrac{r^2}{c}}$که r شعاع چرخش و c فاصله مرکز جرم از محور است. زیرا ویژگی های جرم را حذف می کند و مسئله را به شکل هندسی ساده می کند. مسئله. همه ℓ، c و r کمیت های هندسی هستند.
مرکز پرکاشن نقطه ای بر روی یک جسم متکی به پین است که در آن ضربه عمود بر نقطه محوری نیروی واکنشی ایجاد نمی کند.
نکته جالب دیگری در مورد تعیین شعاع چرخش وجود دارد. شما می توانید از هندسه برای تخمین پاسخ یک جسم صلب به یک ضربه استفاده کنید.rgyr
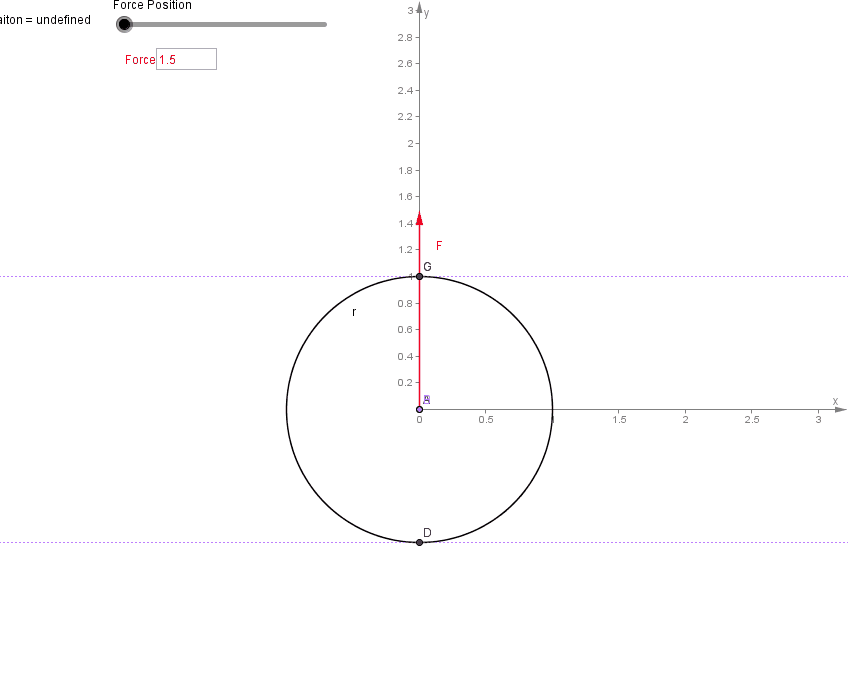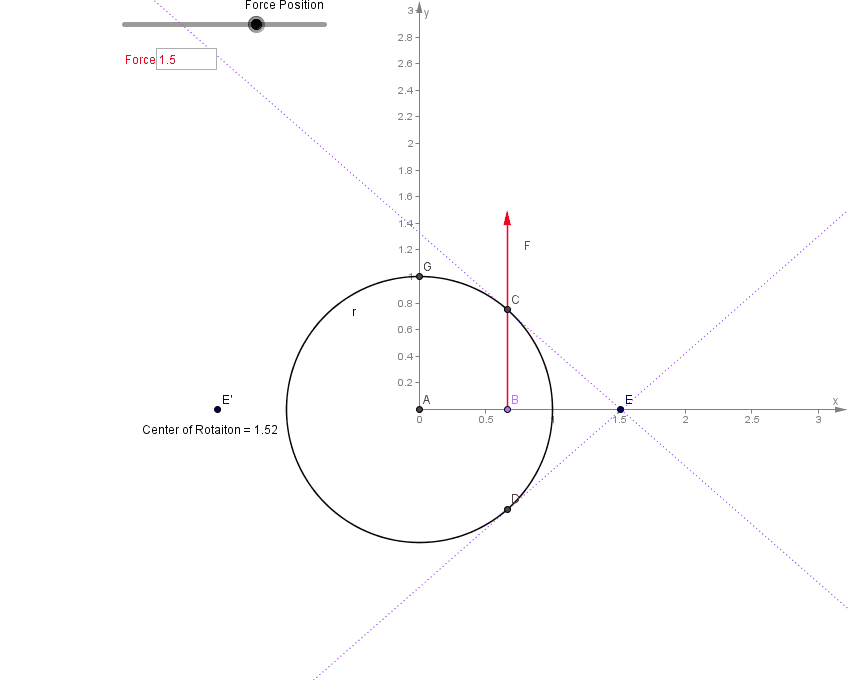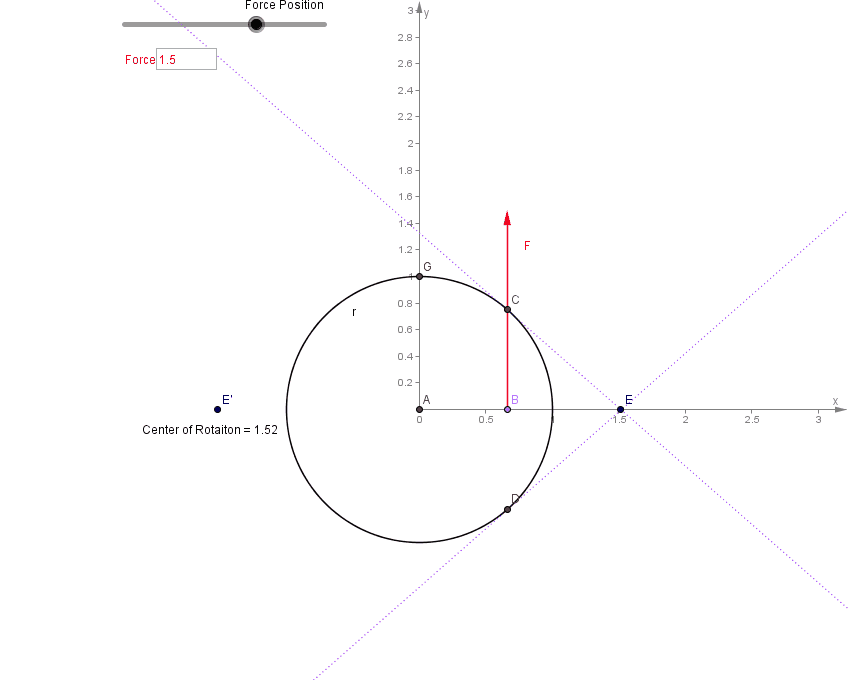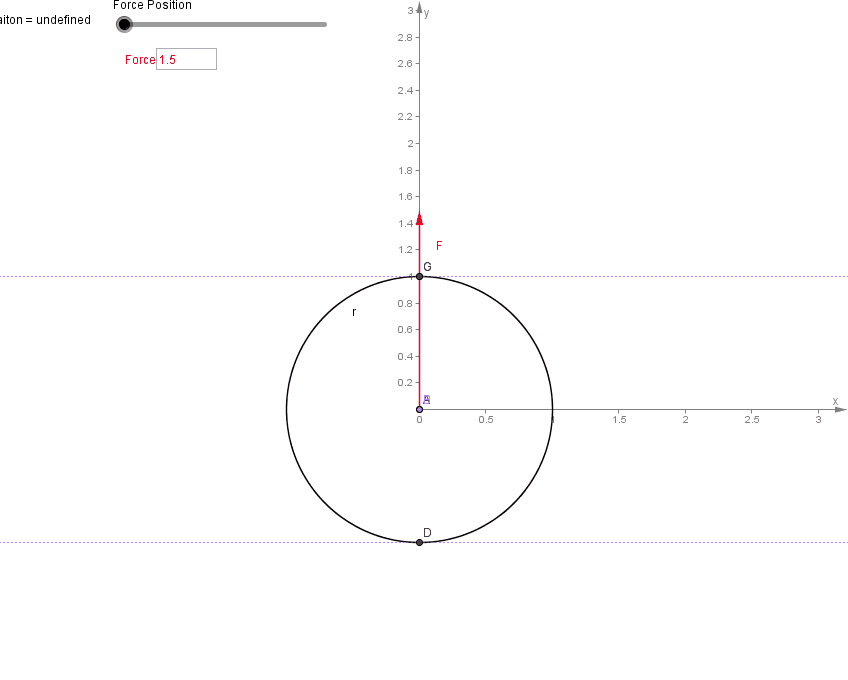
دایره ای به دور مرکز جرم با شعاع r رسم کنید و خط BC را که از طریق آن یک ضربه (یا نیروی لحظه ای) وارد می شود رسم کنید. مماس ها را در جایی که مانند عمل دایره را قطع می کند و محل برخورد آنها نقطه E است رسم کنید. آینه این نقطه (نقطه E' زیر) جایی است که مرکز چرخش است.
بدیهی است که وقتی نیروی اعمال شده از مرکز جرم عبور می کند، مرکز چرخش در بی نهایت است (و بنابراین فقط جسم منتقل می شود). مرکز پرکاشن نقطه ای بر روی یک جسم عظیم گسترده متصل به یک محور است که در آن یک ضربه عمود بر محور هیچ شوک واکنشی ایجاد نمی کند. هنگامی که یک ضربه تکانشی به مرکز ضربه وارد می شود، حرکات چرخشی و انتقالی در محور حرکت خنثی می شوند.نقطه روی یک جسم صلب، معلق است تا بتواند آزادانه حول یک محور ثابت حرکت کند، که در آن ممکن است بدون تغییر موقعیت محور، به جسم ضربه وارد شود.مرکز ضربهای یک آونگ مرکب به عنوان مکانی روی آونگ توصیف میشود که در هنگام اعمال ضربه، شتاب انتقالی صفر را در مفصل محوری نشان میدهد. این مربوط به طول یک آونگ ساده با همان جرم است که فرکانس نوسان یکسانی دارد.یک تیر صلب را تصور کنید که توسط یک فیکسچر از سیم آویزان شده است که می تواند آزادانه در امتداد سیم در نقطه P بلغزد. یک ضربه تکانشی از سمت چپ وارد می شود. اگر زیر مرکز جرم (CM) باشد باعث می شود که میله در خلاف جهت عقربه های ساعت حول CM بچرخد و همچنین باعث می شود که CM به سمت راست حرکت کند. مرکز پرکاشن (CP) زیر CM است. اگر ضربه بالاتر از CP بیفتد، حرکت انتقالی به سمت راست بزرگتر از حرکت چرخشی به سمت چپ در P خواهد بود و باعث می شود که حرکت اولیه خالص فیکسچر به سمت راست باشد. اگر ضربه به زیر CP بیفتد برعکس اتفاق می افتد، حرکت چرخشی در P بزرگتر از حرکت انتقالی خواهد بود و فیکسچر ابتدا به سمت چپ حرکت می کند. تنها در صورتی که ضربه دقیقاً روی CP بیفتد، دو جزء حرکت از بین میروند تا حرکت اولیه خالص صفر در نقطه P ایجاد شود.
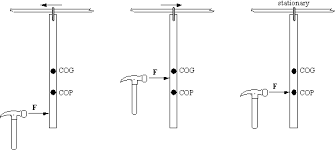
هنگامی که فیکسچر کشویی با محوری جایگزین می شود که نمی تواند به چپ یا راست حرکت کند، یک ضربه ضربه ای در هر جایی به جز در CP منجر می شود.
شعاع چرخش به طور کلی فاصله ای از مرکز جرم یک جسم است که می توان کل جرم را بدون تغییر گشتاور اینرسی چرخشی حول محوری که از مرکز جرم می گذرد، متمرکز کرد.شعاع چرخش برای مقایسه نحوه رفتار اشکال ساختاری مختلف تحت فشار در امتداد یک محور استفاده می شود. برای پیش بینی کمانش در یک عضو فشاری یا تیر استفاده می شود.شکل-A جسمی با جرم M را نشان می دهد که حول محور و شکل راس می چرخد. B نشان می دهد که جرم کل جسم در فاصله K از محور چرخش متمرکز است.اگر به هر میله ای (طول L) با ضربه P در فاصله d زیر مرکز جرم ضربه بزنیم، میله به گونه ای حرکت می کند که نقطه C در ابتدا حرکت نمی کند - به عبارت دیگر چرخشی در حدود C بدست می آوریم. این بدون توجه به توزیع جرم میله صادق است - فقط موقعیت C تغییر خواهد کرد. حفظ تکانه زاویه ای در مورد مرکز جرم می دهد $Pd = I\omega\tag1$
برای چرخش در مورد C می توانیم بنویسیم
$P(x+d) = (I+mx^2)\omega\tag2$
نتیجه می شود که$Px = mx^2\omega$
و$P = mx\omega\tag3$
با ترکیب (1) و (3) به دست می آوریم $mxd = I$
و می دانیم که برای یک میله یکنواخت، $I=\frac{mL^2}{12}$است. بنابراین، هنگامی که میله در انتها ضربه می زند، $d=\frac{L}{2}$ و با حل x متوجه می شویم که مرکز ضربه C در نقطه ای است که $\frac{L}{6}$ بالاتر از مرکز جرم است.
از همین تحلیل می توان به صورت معکوس استفاده کرد: اگر میله را حول نقطه C بچرخانم، اگر به نقطه ای که از مرکز جرم d است ضربه بزنیم، کاملا متوقف می شود. حالا چرا این بیشترین تاثیر را می گذارد؟
به یاد داشته باشید که مرکز جرم یک جسم به گونهای حرکت میکند که انگار تمام نیروهای وارد بر جسم در مرکز جرم عمل میکنند - بنابراین اگر به حرکت مرکز جرم قبل و بعد از ضربه نگاه کنیم، میتوانیم مجموع آن را تعیین کنیم. از نیروهای خارجی بود.
در اینجا دو سناریو وجود دارد - ضربه زدن درست در بالای یا درست زیر مرکز پرکاشن:
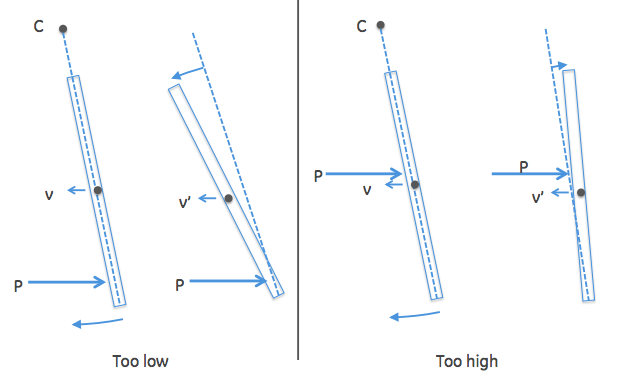
همانطور که می بینید، در هر دو حالت مرکز جرم در جهت اصلی ادامه می یابد، هرچند با سرعت کاهش یافته. این نشان می دهد که ضربه کل $P=m\Delta v$ کمتر از زمانی است که ضربه دقیقاً در مرکز ضربه باشد (که منجر به عدم چرخش پس از ضربه می شد).
در این تصویر، مرکز چرخش C را خارج از شمشیر قرار می دهم - یک تاب خوب با شمشیر پهن که قادر به کشتن زامبی است احتمالاً نیاز به درگیری کامل جسم با باسن و شانه دارد. در آن سناریو فاصله x بزرگ می شود و d باید کوچکتر باشد. هر چه نقطه چرخش دورتر باشد، بیشتر می خواهید به مرکز جرم ضربه بزنید - محصول ثابت می ماند. در مورد توزیع جرم یکنواخت این رابطه است
$xd = \frac{L^2}{12}$
وقتی فاصله را تا نقطه چرخش دوبرابر می کنید، فاصله تا مرکز ضربه را نصف می کنید.
اگر نقطه برخورد در داخل CoP باشد، ثابت نگه داشتن تیغه به نیرویی در جهت ضربه نیاز دارد و از نظر تئوری می تواند منجر به انتقال بیشتر تکانه شود.
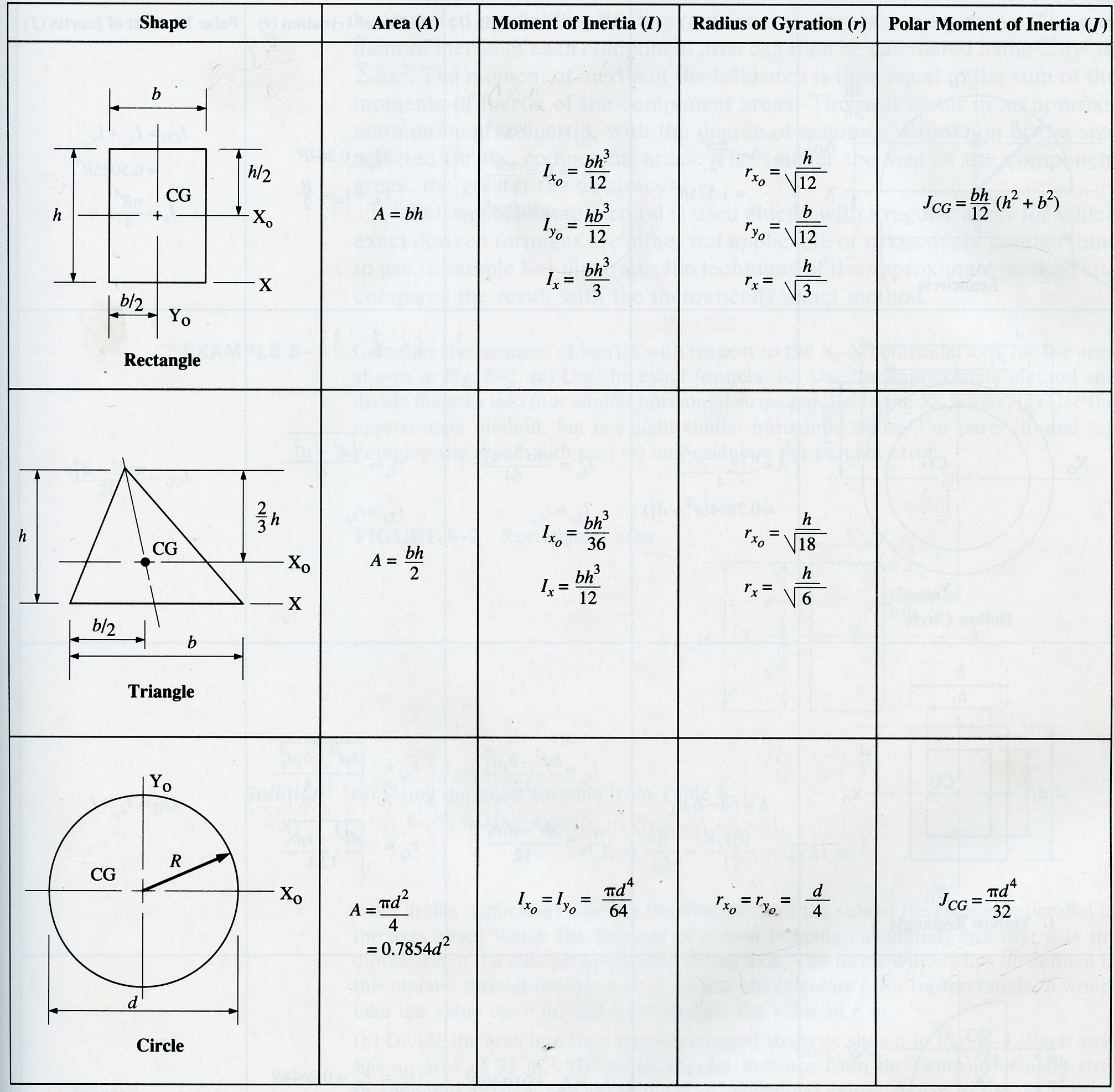
طبق تعریف شعاع چرخش، ممان اینرسی جسم نشان داده شده در شکل-A برابر است با ممان اینرسی جرم نقطه متمرکز (نشان داده شده در شکل B) حول همان محور.$I_{\text{Point mass}}$وشعاع چرخش قطبی:شعاع چرخش قطبی
برای بارگذاری استاتیکی، شعاع قطبی چرخش را می توان با استفاده از فرمول زیر محاسبه کرد:$\sqrt{\frac{I_{o}}{A}}$
طبق شرط شعاع چرخش یک جسم دورانکننده، میتوان شعاعی در نظر گرفت که به نظر برسد کل جرم جسم در یک نقطه متمرکز شده و در فاصلهای برابر با این شعاع نسبت به محور، در حال دوران است. این شعاع تحت عنوان شعاع ژیراسیون (Radius of Gyration) شناخته میشود.شعاع ژیراسیونِ یک جسم (Rg) ، فاصلهای است که اگر کل جرم جسم را در حلقهای یکنواخت با این شعاع توزیع کنیم، در این صورت لختی دورانی آن برابر با لختی دورانی جسمِ اولیه است. در شکل زیر این مفهوم نشان داده شده است.جسمی را در نظر بگیرید که از چندین جرم متمرکز شده به اندازه $m _ 1 , m _ 2 , m _ 3 \ , \ … , \ m _ n$ که در فواصل $r _ 1 , r _ 2 , r _ 3 \ , \ … , \ r _ n$ قرار گرفتهاند، تشکیل شده است. در این صورت میتوان لختی دورانی ایجاد شده در نتیجه هریک از اجرام را محاسبه کرده و با میانگینگیری از آنها، لختی دورانی را بدست آورد. برای چنین جسمی، لختی دورانی برابر است با:$\large { \displaystyle I = m _ { 1 } r _ { 1 } ^ { 2} + m _ { 2} r _ { 2 }^ { 2 } + \cdots + m _ {n } r _ {n } ^ { 2 } }$
حال حالتی را در نظر بگیرید که در آن تمامی جرمها برابر باشند. در این صورت لختی دورانی را میتوان به صورت زیر بازنویسی کرد.
$\large { \displaystyle I = m( r _ { 1 } ^ { 2 }+ r _ { 2} ^ { 2 } + \cdots + r _ { n } ^ { 2 } ) }$
با فرض اینکه رابطه $M = { n } { m }$
نشاندهنده جرم کل جسم باشد، در این صورت میتوان رابطه لختی دورانی را به صورت بازنویسی کرد.
${ \displaystyle I = M ( r _ { 1 } ^ { 2 } + r _ { 2 } ^ { 2 } + \cdots + r _ { n } ^ { 2 } ) / n }$
با توجه به تعریف شعاع ژیراسیون، میتوان لختی بدست آمده در بالا را برابر با لختی ناشی از شعاع ژیراسیون در نظر گرفت. با استفاده از این معادلسازی داریم:
$\large {\displaystyle M R _{ g } ^{ 2 } = M ( r _ { 1 } ^{ 2 } + r _ {2 } ^ { 2 } + \cdots + r _{ n } ^ { 2 } ) / n }$
در نتیجه شعاع ژیراسیون مطابق با رابطه زیر بدست خواهد آمد.
$\large {\displaystyle R _ {g } ^ { 2 } = ( r _ {1 } ^ { 2 } +r _ { 2} ^ { 2 } + \cdots + r _ { n } ^ { 2 } ) / n }$
بنابراین میتوان گفت شعاع ژیراسیون یک جسم متناسب با توان دوم فواصلی است که جرمها از آن قرار گرفتهاند.
کاربردها در مهندسی سازه
در مهندسی سازه، از شعاع ژیراسیون به منظور توصیف نحوه توزیع جرمِ یک مقطع از ستون حول محور دورانش استفاده میشود. در این حالت از رابطه زیر جهت بدست آوردن شعاع ژیراسیون استفاده میشود.
$\large R _ { { { \mathrm { g } } } } = { \sqrt { \left ( { { \frac { I } { A } } } \right ) } }$در رابطه فوق، I نشاندهنده لختی دورانی و Rg، شعاع ژیراسیون را نشان میدهد. در این موارد از مفهوم ژیراسیون برای تخمین زدن اندازه سختی ستون نیز استفاده میشود. اگر گشتاورهای دورانی تانسور ژیراسیون حول دو محور برابر نباشند، در این صورت تیر حول محوری خم خواهد شد که گشتاور دورانی حول آن کمتر باشد. برای نمونه تیری با مقطعی بیضی شکل، حول محور کوتاهترش خم خواهد شد.
در مهندسی معمولا با اجسامی سر و کار داریم که در آنها توزیع جرم به صورت پیوسته است. بنابراین در چنین مواردی میتوان با استفاده از انتگرال، شعاع ژیراسیون را بدست آورد.
کاربردها در مکانیک و فیزیک
در مکانیک معمولا از شعاع ژیراسیون به منظور تحلیل حرکت اجسام پیچیده استفاده میشود. در چنین اجسامی میزان شتاب زاویهای یا خطی جسم وابسته به لختی دورانی جسم حول محورهای مختلف است. از این رو از شعاع ژیراسیون به منظور تحلیل حرکت جسم در حالتی استفاده کرد که در آن توزیع جرمی جسم به صورت یکنواخت در نظر گرفته میشود.
در این موارد نیز از یکی از روابط زیر بهمنظور بدست آوردن لختی دورانی استفاده میشود.
$\large r _ { { { \mathrm { g } } { \text { axis}} } } ^ { { 2 } } = { \frac { I _ { { \text {axis} } } } { m } }$
$\large r _ { { { \mathrm { g } } { \text { axis } } } } = { \sqrt { { \frac { I _ { { \text {axis} } } }{ m} } } }$
توجه داشته باشید که در رابطه فوق، $I _ { {\text{axis}} }$
اسکالر بوده و برابر با تانسور گشتاور اینرسی نیست. جالب است بدانید که شعاع ژیراسیون دارای کاربردهایی مولکولی نیز است. در حقیقت در فیزیک پلیمری از شعاع ژیراسیون به منظور توصیف ابعاد زنجیره پلیمری استفاده میشود. برای نمونه شعاع زنجیره پلیمری یک مولکول در لحظهای مشخص برابر است با:$\large { \displaystyle R _ { \mathrm { g } } ^ { 2 } \ { \stackrel {\mathrm {def} } {=}}\ { \frac { 1 } { N } } \sum _ { k = 1 } ^ { N } \left ( \mathbf { r } _ { k } – \mathbf { r } _ { \mathrm {mean} } \right ) ^ { 2 } }$در عبارت فوق، $r _ { mean }$
، نشاندهنده فاصله میانگین مونومرها است. همانطور که در ادامه نیز نشان داده شده، شعاع ژیراسیون وابسته به توان دوم فاصله مونومرها از یکدیگر نیز است.$\large { \displaystyle R _ { \mathrm { g } } ^ { 2 } \ {\stackrel {\mathrm { def } } { = } } \ {\frac { 1 } { 2 N ^ { 2 } } } \sum _{i,j}\left(\mathbf {r} _{i}-\mathbf { r } _ { j } \right ) ^ { 2 } }$
البته به عنوان روشی جایگزین میتوان با جمع زدن گشتاورهای اصلی تانسور ژیراسیون نیز شعاع ژیراسیون را بدست آورد.
ممان اینرسی و مرکز چرخش چیه
مرکز جرم نقطه ای در جسم صلب است که می توان تمام جرم را در آن متمرکز کرد و سپس حرکت انتقالی) جسم به عنوان یک کل را از آن نقطه توصیف کرد.
با این حال نمی توان همین را در مورد مرکز چرخش گفت زیرا با تغییر در انتخاب محور چرخش ما تغییر می کند. پس آیا من آن را اشتباه تصور می کنم؟ معنای درست ممان اینرسی و مرکز چرخش چیست؟ نمایش های بصری ترجیح داده می شوند. با تشکر.
ممان اینرسی در معنای ساده به معنای مقاومتی است که یک جسم در برابر هر تغییری که حالت چرخش آن را مختل کند، ارائه می دهد. این همان هدف جرم در حرکت خطی غیر چرخشی است. جرم بیشتر به معنای اینرسی بیشتر است. اینرسی فقط به معنای مقاومت است.
به عنوان مثال، هنگامی که ممان اینرسی یک دیسک دایره ای را در مورد مرکز آن محاسبه می کنید، فقط ممان اینرسی تمام جرم های بی نهایت کوچکی را که دیسک را تشکیل می دهند، اضافه می کنید. این به شما ممان اینرسی کل دیسک را می دهد.
$I=\frac{MR^2}{2}$
حال اگر می خواهید این دیسک را با یک جرم نقطه ای با همان جرم دیسک جایگزین کنید، به طوری که مقدار گشتاور اینرسی را حول همان محور بدست آورید، تنها کاری که باید انجام دهید این است که این جرم نقطه ای را در چنین نقطه ای قرار دهید. فاصله ای از محوری که همان MOI را به شما می دهد.
ممان اینرسی یک جرم نقطه ای با mr2 به دست می آید که r فاصله عمود جرم نقطه از محور چرخش است.
با توجه به اظهارات قبلی،
$mr^2=(MOI)_{disc}$
$mr^2=\frac{MR^2}{2}$
$r^2=\frac{R^2}{2}$
$r=\frac{R}{\sqrt 2}$
در اینجا r شعاع چرخش نامیده می شود. مرکز چرخش را با محور چرخش اشتباه نگیرید.
MOI و شعاع چرخش با محور چرخش تغییر می کند و بدون محور مرجع نمی توان آنها را تعریف کرد. COM یک جرم نقطه ای ساده با جرم یک جسم است که بدون توجه به اینکه نیرو در کجا به جسم صلب وارد می شود، شتابی برابر با جسم صلب در هنگام وارد شدن نیرو به شما می دهد..hope I helped you understand the question. Roham Hesami, sixth
semester of aerospace engineering




