سلام
اگر یک دایره کوچک را حول یک دایره بزرگ بگردانیم و از نقطه تماس دو دایره خطی رسم کنیم به علت اینکه در طی یک دور زدن چند بار حول دایره بزرگ میگردد شکل حاصل شکلی شبیه گل خواهد بود:
حال اگر دو دایره هم اندازه باشند دایره در طی یک چرخش یک بار حول دایره دیگر میگردد و شکل حاصله دلگون خواهد بود:
حال اگر دایره چرخان بزرگتر از دایره ثابت باشد در طی یک چرخش کمتر از یک بار دور دایره دیگر میزند و شکل حاصله مارپیچ خواهد بود:
حال سوال جالب این است که در چه شرایطی این مارپیچ فیبوناچی خواهد بود؟
سوالی جالب
- Simplexity
عضویت : دوشنبه ۱۴۰۲/۵/۹ - ۲۰:۵۸
پست: 29-
سپاس: 2
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3289-
سپاس: 5494
- جنسیت:
تماس:
Re: سوالی جالب
r: شعاع هر دایره در حال چرخش.
d: فاصله بین نقطه چرخش و مراکز دایره.اگرr=d، سپس دایره های در حال چرخش همگی در مرکز به هم می رسند.اگرr<d، سپس یک سوراخ کوچکتر در داخل دایره اصلی وجود خواهد داشت.؟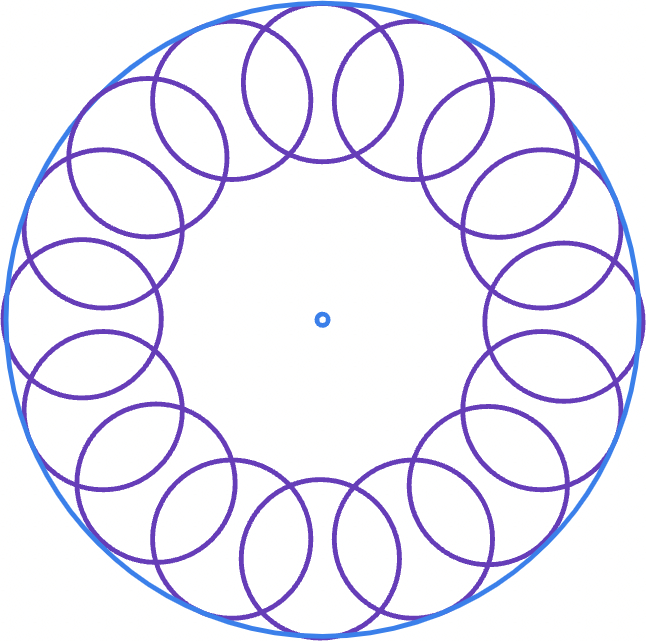
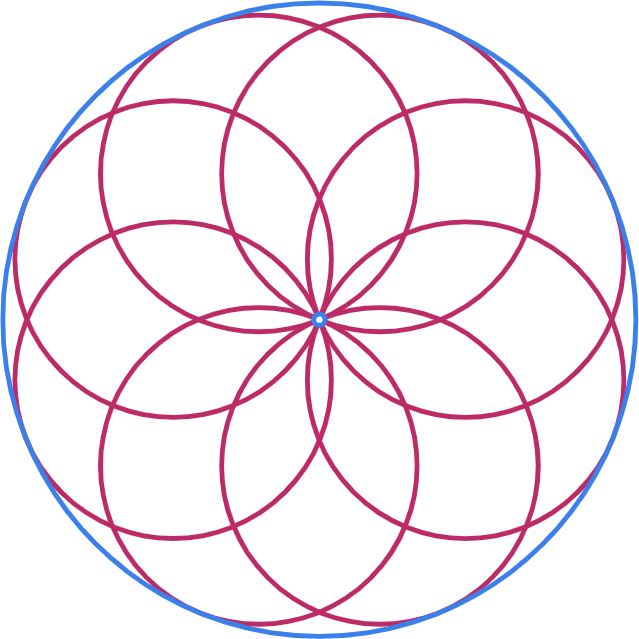
.ترسیم نمودار یک گل با معادلات قطبی و پارامتری
در تلاش برای پاسخ به این سوال جالب اما رها شده، با مشکل عجیبی روبرو شدم که قبلاً هرگز ندیده بودم و نمی دانم چگونه آن را حل کنم.
برای برخی زمینهها، این سؤال حاوی تصویری از یک گل است و میپرسد چگونه میتوان گل را دقیقاً در مختصات قطبی ترسیم کرد. OP در یک نظر به ایده ترسیم بیضی های منفرد برای مطابقت با شکل و موقعیت هر گلبرگ اشاره می کند. من فکر کردم که این ایده هوشمندانه ای بود، بنابراین با معادله یک بیضی در مختصات مستطیلی به طور کلی شروع کردم و با تبدیل آن به مختصات قطبی شروع به کار کردم:
$\frac{(x\cos\phi-y\sin\phi-h)^2}{a^2}+\frac{(x\sin\phi+y\cos\phi-k)^2}{b^2}=c^2$
در این مورد، a نصف طول محوری است که در امتداد x قرار دارد-محور، b نصف طول محوری است که در امتداد y قرار داردمحور، h جابجایی افقی، k است جابجایی عمودی است و ϕ زاویه چرخش حول مبدا است.من برای این سوال کاملاً نامرتبط روی Desmos تحقیق می کردم که متوجه شدم روش محدود کردن دامنه و محدوده ای که در نهایت برای پاسخ به آن سوال استفاده کردم، در اینجا نیز کاملاً کار می کند. من مجبور شدم به ورژن هاب مستطیلی معادلات گلبرگ سوئیچ کنم
فقط به عنوان یک مثال سریع من در نهایت به ارائه نمودار پرداختم
$x^2+y^2=1.21$
$\begin{align}
\frac{(x\cos\phi_1-y\sin\phi_1-h_1)^2}{a_1^2}+\frac{(y\cos\phi_1+x\sin\phi_1-k_1)^2}{b_1^2}&=c_1^2\{x\le-0.5\}\{y\ge0.96465\} \\
\frac{(x\cos\phi_1-y\sin\phi_1-h_1)^2}{a_1^2}+\frac{(y\cos\phi_1+x\sin\phi_1-k_1)^2}{b_1^2}&=c_1^2\{x\ge-0.49999\}\{y\ge1.09571\} \\
\frac{(x\cos\phi_2-y\sin\phi_2-h_2)^2}{a_2^2}+\frac{(y\cos\phi_2+x\sin\phi_2-k_2)^2}{b_2^2}&=c_2^2\{x\le-1.29445\} \\
\frac{(x\cos\phi_2-y\sin\phi_2-h_2)^2}{a_2^2}+\frac{(y\cos\phi_2+x\sin\phi_2-k_2)^2}{b_2^2}&=c_2^2\{x\le-0.99377\}\{y\le0.47522\} \\
\frac{(x\cos\phi_2-y\sin\phi_2-h_2)^2}{a_2^2}+\frac{(y\cos\phi_2+x\sin\phi_2-k_2)^2}{b_2^2}&=c_2^2\{x\ge-0.72153\}\{y\ge0.84065\}
\end{align}$
برای به دست آوردن مرکز و دو گلبرگ اول، و نتیجه دقیقاً شبیه چیزی بود که انتظارش را داشتم:

d: فاصله بین نقطه چرخش و مراکز دایره.اگرr=d، سپس دایره های در حال چرخش همگی در مرکز به هم می رسند.اگرr<d، سپس یک سوراخ کوچکتر در داخل دایره اصلی وجود خواهد داشت.؟


.ترسیم نمودار یک گل با معادلات قطبی و پارامتری
در تلاش برای پاسخ به این سوال جالب اما رها شده، با مشکل عجیبی روبرو شدم که قبلاً هرگز ندیده بودم و نمی دانم چگونه آن را حل کنم.
برای برخی زمینهها، این سؤال حاوی تصویری از یک گل است و میپرسد چگونه میتوان گل را دقیقاً در مختصات قطبی ترسیم کرد. OP در یک نظر به ایده ترسیم بیضی های منفرد برای مطابقت با شکل و موقعیت هر گلبرگ اشاره می کند. من فکر کردم که این ایده هوشمندانه ای بود، بنابراین با معادله یک بیضی در مختصات مستطیلی به طور کلی شروع کردم و با تبدیل آن به مختصات قطبی شروع به کار کردم:
$\frac{(x\cos\phi-y\sin\phi-h)^2}{a^2}+\frac{(x\sin\phi+y\cos\phi-k)^2}{b^2}=c^2$
در این مورد، a نصف طول محوری است که در امتداد x قرار دارد-محور، b نصف طول محوری است که در امتداد y قرار داردمحور، h جابجایی افقی، k است جابجایی عمودی است و ϕ زاویه چرخش حول مبدا است.من برای این سوال کاملاً نامرتبط روی Desmos تحقیق می کردم که متوجه شدم روش محدود کردن دامنه و محدوده ای که در نهایت برای پاسخ به آن سوال استفاده کردم، در اینجا نیز کاملاً کار می کند. من مجبور شدم به ورژن هاب مستطیلی معادلات گلبرگ سوئیچ کنم
فقط به عنوان یک مثال سریع من در نهایت به ارائه نمودار پرداختم
$x^2+y^2=1.21$
$\begin{align}
\frac{(x\cos\phi_1-y\sin\phi_1-h_1)^2}{a_1^2}+\frac{(y\cos\phi_1+x\sin\phi_1-k_1)^2}{b_1^2}&=c_1^2\{x\le-0.5\}\{y\ge0.96465\} \\
\frac{(x\cos\phi_1-y\sin\phi_1-h_1)^2}{a_1^2}+\frac{(y\cos\phi_1+x\sin\phi_1-k_1)^2}{b_1^2}&=c_1^2\{x\ge-0.49999\}\{y\ge1.09571\} \\
\frac{(x\cos\phi_2-y\sin\phi_2-h_2)^2}{a_2^2}+\frac{(y\cos\phi_2+x\sin\phi_2-k_2)^2}{b_2^2}&=c_2^2\{x\le-1.29445\} \\
\frac{(x\cos\phi_2-y\sin\phi_2-h_2)^2}{a_2^2}+\frac{(y\cos\phi_2+x\sin\phi_2-k_2)^2}{b_2^2}&=c_2^2\{x\le-0.99377\}\{y\le0.47522\} \\
\frac{(x\cos\phi_2-y\sin\phi_2-h_2)^2}{a_2^2}+\frac{(y\cos\phi_2+x\sin\phi_2-k_2)^2}{b_2^2}&=c_2^2\{x\ge-0.72153\}\{y\ge0.84065\}
\end{align}$
برای به دست آوردن مرکز و دو گلبرگ اول، و نتیجه دقیقاً شبیه چیزی بود که انتظارش را داشتم:


- Simplexity
عضویت : دوشنبه ۱۴۰۲/۵/۹ - ۲۰:۵۸
پست: 29-
سپاس: 2
Re: سوالی جالب
جوابتون ربطی به سوال من نداشت اگه سوال مفهوم نیست تا بیشتر توضیح بدم.
سوال من این بود که شعاع دو دایره چه نسبتی با هم باید داشته باشند تا حاصل چرخش مارپیچ فیبوناچی شود؟
سوال من این بود که شعاع دو دایره چه نسبتی با هم باید داشته باشند تا حاصل چرخش مارپیچ فیبوناچی شود؟
شما دسترسی جهت مشاهده فایل پیوست این پست را ندارید.
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3289-
سپاس: 5494
- جنسیت:
تماس:
Re: سوالی جالب
اجازه دهید r برای شعاع یکی از دایره های کوچک و R نشان دهنده شعاع نیم دایره بزرگ است.
هیپوتانوز مثلث .بنابراین شعاع R از نیم دایره نسبت طلایی در حال حاضر نسبت طلایی به نظر می رسه درسته؟ فقط یک مرحله دیگر: نسبت R (شعاع نیم دایره) تا 2r (قطر یک دایره کوچک) است$\phi = (1 + \sqrt 5)/2$
نقاط متوالی با زاویه طلایی چرخانده می شوند که$(1 - 1/\phi)$ است.هفتم یک دور کامل، که در آن $\phi = (1 + \sqrt 5)/2$
که =1.618033989…=ϕ میشه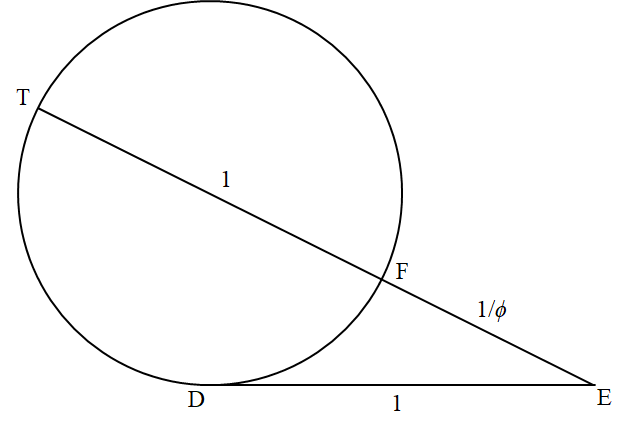
در این شکل FT قطر دایره ای به قطر 1 است نقاط E,F,T خطی هستند و بخش ED دارای طول 1 و مماس بر دایره D است.یک قضیه هندسه وجود دارد که می گوید$EF \times ET = (ED)^2, \tag1$
اما از آنجایی که ED=1 معادله 1) دلالت دارد$EF = \frac1{ET},$اما آرایش خطی E,F,T سپس به ما می گوید که ET=EF+1; از این رو$ET = \frac1{ET} + 1. \tag2$تنها یک جواب مثبت معادله (2) وجود دارد.
$ET = \phi,$ است جایی که ϕ نسبت طلایی است نتیجه می شود که$EF = 1/\phi.$.حالا شکل زیر را در نظر بگیرین
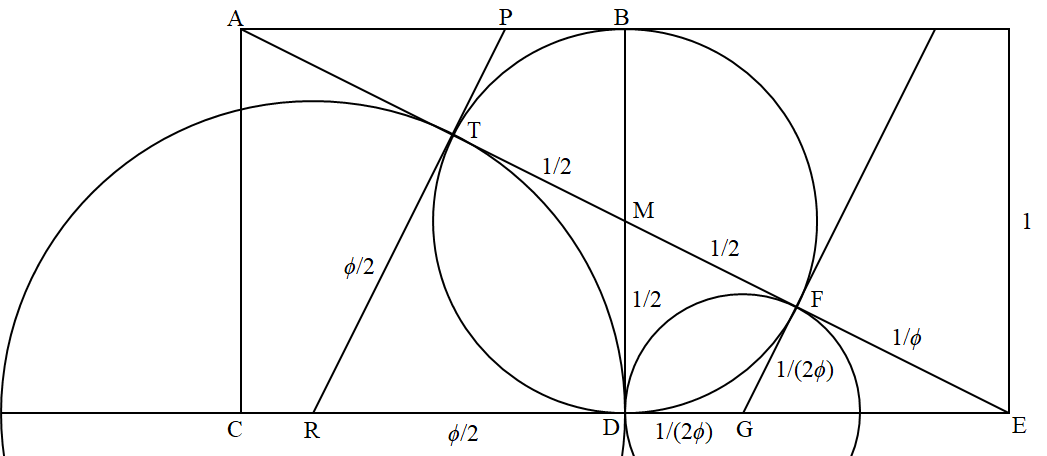
این مربع شماست (اسم رئوس را با حروف بزرگ A,B,C,D نوشتم با اضافه شدن چند نام به برخی نکات و با اضافه شدن مقداری ساخت اضافی به آن. به طور مشخص M نقطه وسط BD است
T نقطه مماس AM است با دایره در مورد R شعاع RT تا نقطه P گسترش می یابد در AB یک دایره بر روی قطر BD ساخته شده است با مرکز M مربع دیگری در طرف دیگر BD به هم متصل است بخش AM
به راس E گسترش یافته است از مربع مجاور که دایره دور M را قطع می کند در F مماس بر آن دایره در F DE را قطع می کند در G و دایره ای با مرکز G ساخته شده است و شعاع FG.
برای سادگی من برای این رقم x=1 فرض کرده ام و ضلع مربع را بر این اساس برچسب زد. فقط تمام طول های شکل را در x ضرب کنید
به منظور به دست آوردن طول های "واقعی" که توسط بیان مسئله شما ذکر شده است.با بررسی مماس بر دایره ها$MD = MT = \frac12,$ داریم
و همچنین GD=GF که به این معنی است که دایره اطراف M دقیقاً از T عبور می کند و همچنین دایره های اطراف R و F بر روی D مماس متقابل هستند.توجه کنید که یک کپی از شکل اول در شکل دوم تعبیه شده است. این به این معنی است که ET=φ و$EF = 1/\phi.$همچنین توجه کنید که مثلث $\triangle EFG,$,$\triangle EDM,$.$\triangle ETR$
شبیه هستند. (اندازه آنها اتفاقاً در پیشرفت هندسی $\frac1\phi : 1 : \phi,$ است همچنین توجه کنین که $DM = \frac12 DE$
و بنابراین $FG = \frac12 EF = \frac1{2\phi}$ و$TR = \frac12 ET = \frac12 \phi,$ این چیزی است که شما می خواستید نشان دهید.
هیپوتانوز مثلث .بنابراین شعاع R از نیم دایره نسبت طلایی در حال حاضر نسبت طلایی به نظر می رسه درسته؟ فقط یک مرحله دیگر: نسبت R (شعاع نیم دایره) تا 2r (قطر یک دایره کوچک) است$\phi = (1 + \sqrt 5)/2$
نقاط متوالی با زاویه طلایی چرخانده می شوند که$(1 - 1/\phi)$ است.هفتم یک دور کامل، که در آن $\phi = (1 + \sqrt 5)/2$
که =1.618033989…=ϕ میشه

در این شکل FT قطر دایره ای به قطر 1 است نقاط E,F,T خطی هستند و بخش ED دارای طول 1 و مماس بر دایره D است.یک قضیه هندسه وجود دارد که می گوید$EF \times ET = (ED)^2, \tag1$
اما از آنجایی که ED=1 معادله 1) دلالت دارد$EF = \frac1{ET},$اما آرایش خطی E,F,T سپس به ما می گوید که ET=EF+1; از این رو$ET = \frac1{ET} + 1. \tag2$تنها یک جواب مثبت معادله (2) وجود دارد.
$ET = \phi,$ است جایی که ϕ نسبت طلایی است نتیجه می شود که$EF = 1/\phi.$.حالا شکل زیر را در نظر بگیرین

این مربع شماست (اسم رئوس را با حروف بزرگ A,B,C,D نوشتم با اضافه شدن چند نام به برخی نکات و با اضافه شدن مقداری ساخت اضافی به آن. به طور مشخص M نقطه وسط BD است
T نقطه مماس AM است با دایره در مورد R شعاع RT تا نقطه P گسترش می یابد در AB یک دایره بر روی قطر BD ساخته شده است با مرکز M مربع دیگری در طرف دیگر BD به هم متصل است بخش AM
به راس E گسترش یافته است از مربع مجاور که دایره دور M را قطع می کند در F مماس بر آن دایره در F DE را قطع می کند در G و دایره ای با مرکز G ساخته شده است و شعاع FG.
برای سادگی من برای این رقم x=1 فرض کرده ام و ضلع مربع را بر این اساس برچسب زد. فقط تمام طول های شکل را در x ضرب کنید
به منظور به دست آوردن طول های "واقعی" که توسط بیان مسئله شما ذکر شده است.با بررسی مماس بر دایره ها$MD = MT = \frac12,$ داریم
و همچنین GD=GF که به این معنی است که دایره اطراف M دقیقاً از T عبور می کند و همچنین دایره های اطراف R و F بر روی D مماس متقابل هستند.توجه کنید که یک کپی از شکل اول در شکل دوم تعبیه شده است. این به این معنی است که ET=φ و$EF = 1/\phi.$همچنین توجه کنید که مثلث $\triangle EFG,$,$\triangle EDM,$.$\triangle ETR$
شبیه هستند. (اندازه آنها اتفاقاً در پیشرفت هندسی $\frac1\phi : 1 : \phi,$ است همچنین توجه کنین که $DM = \frac12 DE$
و بنابراین $FG = \frac12 EF = \frac1{2\phi}$ و$TR = \frac12 ET = \frac12 \phi,$ این چیزی است که شما می خواستید نشان دهید.

- Simplexity
عضویت : دوشنبه ۱۴۰۲/۵/۹ - ۲۰:۵۸
پست: 29-
سپاس: 2
Re: سوالی جالب
یعنی اگر شعاع دایره بزرگ phi/2 و شعاع دایره کوچک 1/2phi باشد و دایره بزرگ دور دایره کوچک بچرخد مارپیچ طلایی ایجاد میشود؟!
میتونی این را برایم اثباتش کنی یا توسط برنامه نویسی ترسیمش کنی؟مرسی
میتونی این را برایم اثباتش کنی یا توسط برنامه نویسی ترسیمش کنی؟مرسی
- rohamavation
نام: roham hesami radرهام حسامی راد
محل اقامت: 100 مایلی شمال لندن جاده آیلستون، لستر، لسترشر. LE2
عضویت : سهشنبه ۱۳۹۹/۸/۲۰ - ۰۸:۳۴
پست: 3289-
سپاس: 5494
- جنسیت:
تماس:
Re: سوالی جالب
معادلات پارامتری، $x,\ y=\sin(t)·φ^{t/π},\ \cos(t)·φ^{t/π}$
یک مارپیچ ایجاد میکنه که در آن فاصله بین قوس ها رشد میکنه کوچک میشه و به تدریج به توان φ میرسه در هر مضرب $π$ (هر 180 درجه).
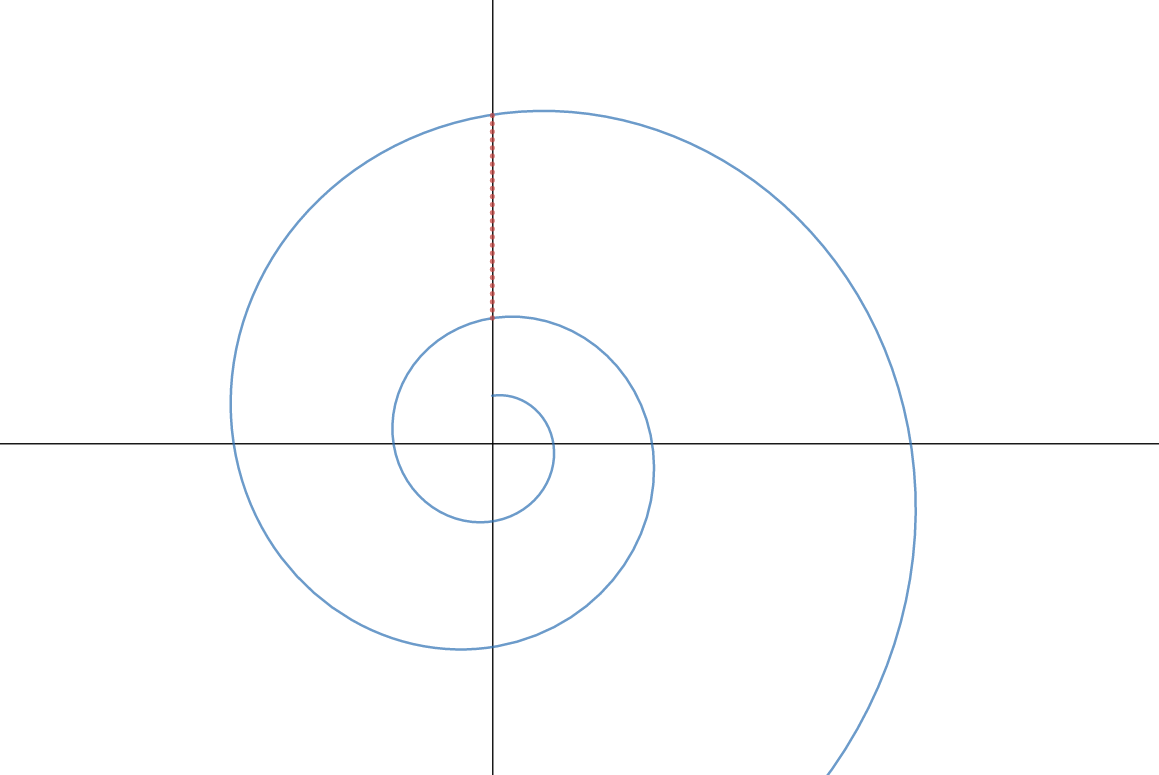
من میخوام معادلات پارامتری را برای یک مارپیچ پیدا کنم که در آن این فاصله با توان φ دقیقاً به همان صورت نسبت به مضرب زاویه طلایی، یعنی$\frac{2π}{φ}$ رشد میکنه کوچک میشه
(به جای انجام این کار نسبت به $π$و. φ به صورت $φ=\left(\frac{1+5^{1/2}}{2}\right)$ تعریف میکنم
اگر من مختصات قطبی را در نظر بگیرم $(r,\theta)=(f(t),t)$ با شرط اولیه که منحنی از آن عبور کند$(x,y)=(b,0)$سپس رابطه تعیین کننده منحنیه $f(k\omega) - f(k\omega-2\pi) = \phi^{k+c} = \exp_\phi(k+c) \qquad\qquad f(0) = b\tag{roham1}$جایی که$\omega := 2\pi/\phi$،$k$ یک عدد صحیحه و c فقط برای اطمینان از مضرب ω وجود داره مطابقت با توانهای مناسب ϕ. پیوسته k
$f(t)-f(t-2\pi) = \exp_\phi\left(\frac{t}{\omega}+c\right) \qquad\qquad f(0)=b \tag{roham2}$
فرض کن راه حل دارای فرم$f(t) = a\left(\phi^{t/\omega}-1\right) + b \tag{roham3}$سپس (2roham) نیاز داره$\exp_\phi\left(\frac{t}{\omega}+c\right) = a\exp_\phi\left(\frac{t}{\omega}\right) - a\exp_\phi\left(\frac{t}{\omega}-\frac{2\pi}{\omega}\right)
= a\exp_\phi\left(\frac{t}{\omega}\right) - a\exp_\phi\left(\frac{t}{\omega}-\phi\right) \tag{roham4}$تقسیم سمت چپ ترین و راست ترین عبارات بر$\phi^{t/\omega}$
$\phi^c = a - a\phi^{-\phi} \qquad\to\qquad a = \frac{\phi^{\phi+c}}{\phi^\phi-1}\tag{5}$
به طوری که (3roham) تبدیل میشه$f(t) = \frac{\phi^{\phi+c}}{\phi^\phi-1}\left(\phi^{t/\omega}-1\right) + b \tag{$\star$}$
یک شکل گل را ببینw=9;axis([-w,w,-w,w,-1,1])
L=-w:0.1:w;
f=@(z)(min(1./abs(z).^(2),1));
[X,Y]=meshgrid(L);
Z=X+i*Y;
U=zeros(length(L));
r1=3.4;w1=1.8;
r2=4.5;w2=-0.88;
z1=r1*exp(i*2*a*(0:4));
z2=r2*exp(i*a*(1:2:9));
plot(z1,'*r');plot(z2,'*b');
for k=1:5
U=U+w1*f(Z-z1(k))+w2*f(Z-z2(k));
end;
contour(X,Y,U,3, 'k')
$\begin{align*}
x(t) &= \bigl(1.75 + \cos(5t))\cos\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr), \\
y(t) &= \bigl(1.75 + \cos(5t))\sin\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr),
\end{align*}$
$\begin{align*}
x(t) &= \bigl(1.75 + \cos(5t))\cos\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr), \\
y(t) &= \bigl(1.75 + \cos(5t))\sin\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr),
\end{align*}$

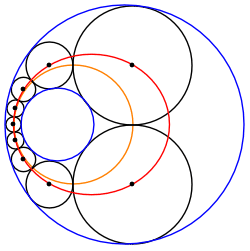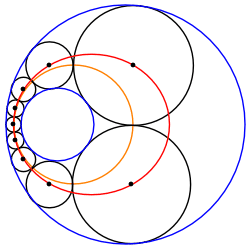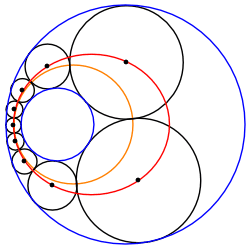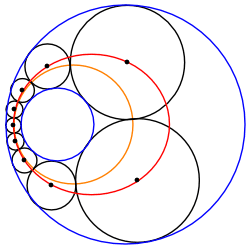
در هندسه زنجیره اشتاینر مجموعهای از n دایره است که همگی بر دو دایره غیر متقاطع مماس هستن آبی و قرمز که در آن n محدوده و هر دایره در زنجیره مماس بر دایره قبلی است.اگر حداقل یک زنجیره بسته اشتاینر از n دایره برای دو دایره مفروض α و β وجود داشته باشه آنگاه تعداد نامتناهی زنجیره اشتاینر بسته از n دایره وجود داره و هر دایره ای مماس بر α و β به همان شکل عضوی از چنین زنجیره ایه
ساده ترین نوع زنجیره اشتاینر خوب یک زنجیره بسته از n دایره با اندازه مساوی است که یک دایره محاطی به شعاع r را احاطه کرده . زنجیر دایرهها بهخودی خود توسط دایرهای به شعاع R احاطه شده دایرههای محاط شده و محصور شده متحدالمرکز هستن و دایرههای زنجیره اشتاینر در حلقۀ بین آنها قرار دارن با تقارن، زاویه 2θ بین مراکز دایره های زنجیره اشتاینر 360 درجه بر n . چون که دایره های زنجیره اشتاینر بر یکدیگر مماس هستن فاصله بین مراکز آنها برابره با مجموع شعاعشون در اینجا دو برابر شعاع ρ آنها. نیمساز دو مثلث قائم الزاویه با زاویه مرکزی θ = 180 درجه / n ایجاد میکنه سینوس این زاویه را می توان به عنوان طول قطعه مقابل آن تقسیم بر هپوتنوز مثلث قائم الزاویه نوشت.$\sin \theta ={\frac {\rho }{r+\rho }}$و$\rho ={\frac {r\sin \theta }{1-\sin \theta }}$نقاط مماس یک دایره زنجیره ای اشتاینر با دایره های داده شده درونی و بیرونی روی خطی قرار دارن که از مرکز مشترک آنها می گذره. لذا شعاع بیرونی R = r + 2ρ.یک زنجیره بسته اشتاینر از n دایره باید که نسبت شعاع R/r دایره های داده شده دقیقاً برابر باشه شما نسبت عدد طلایی بزار${\frac {R}{r}}=1+{\frac {2\sin \theta }{1-\sin \theta }}={\frac {1+\sin \theta }{1-\sin \theta }}=\left[\sec \theta +\tan \theta \right]^{{2}}$برای دایره های متحدالمرکز این فاصله به عنوان لگاریتم نسبت شعاع آنها تعریف بکنید$\delta =\ln {\frac {R}{r}}$پس $\delta =2\ln \left(\sec \theta +\tan \theta \right).$اگر یک زنجیره اشتاینر حلقوی چندحلقه ای n دایره کل داشته باشه و قبل از بسته شدن به دور m بار بپیچد زاویه بین دایره های زنجیره اشتاینر برابره$∘\theta ={\frac {m}{n}}180^{{\circ }}$
با پایتون یک گل رسم کردم
برنامه
from PIL import Image, ImageDraw
import numpy as np
import matplotlib.pyplot as plt
def draw_fractal(s, ls):
# Create a new image with a white background
image = Image.new('RGBA', (s, s), color = (0, 0, 0, 0))
draw = ImageDraw.Draw(image)
# Begin the recursion
draw_fractal_recursive(draw, s/2, s/2, s/2, 0, ls, s)
# Display the image
plt.imshow(np.array(image))
plt.show()
def draw_fractal_recursive(draw, x, y, o, depth, ls, s):
if depth >= len(ls):
return
# Chain order to corresponding order in input list
n = ls[depth]
# Calculate inner base circle radius
i = (o-o*np.sin(np.pi/n))/(np.sin(np.pi/n)+1)
# Fill based on depth
rgba_color = (0, 0, 0, int(255 * np.power(depth/len(ls), 4)))
# Draw circle
draw.ellipse((x-o, y-o, x+o, y+o), fill=rgba_color)
# Recurse on inner circle
draw_fractal_recursive(draw, x, y, i, depth+1, ls, s)
# Loop through all circles of the chain
for r in range(n):
# Translate origin to middle of the 2 base circles
new_x = x + (o+i)/2 * np.cos(2 * np.pi * r / n)
new_y = y + (o+i)/2 * np.sin(2 * np.pi * r / n)
# Recurse on chain circle
draw_fractal_recursive(draw, new_x, new_y, (o-i)/2, depth+1, ls, s)
# Call the function
draw_fractal(600,[13,7,11,5,3])
من یک دایره C1 با قطر مشخص d1 دارم. آن دایره توسط N دایره (C2) با قطر مجهول d2 احاطه شده که در آن هر یک از دایره های C2 دو دایره C2 همسایه و دایره C1 را در یک نقطه مماسند من حالا. باید d2 را پیدا کنم$\cos\left(\frac{360}{N}\right)= \frac{2(r_1+r_2)^2 -(2r_2)^2}{2(r_1+r_2)^2}$.
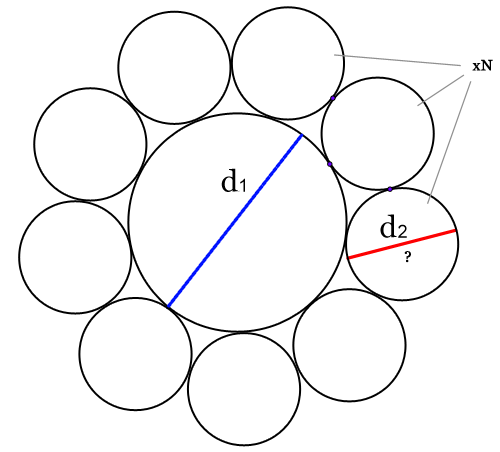
که به راحتی با هندسه پایه قابل حله این یک مورد خاص از زنجیره n استاینرهدو دایره با شعاع r<R داده میشه وفاصله بین مراکز آنها d در زنجیره اشتاینر از n دایره ها پارامترهای ذکر شده باید با این معادله مطابقت داشته خوب
$\begin{align}
d^2&=(R-r)^2-4Rr\tan^2\tfrac\pi{n}
\tag{roham hesami1}\label{1}
.\end{align}$برای مورد خاص داده شده،هم شعاع دایره داخلی r و فاصله d=0بنابراین، شعاع R دایره بیرونی را میتونم $\begin{align}
R&=r\cdot\left(\frac{1+\sin\tfrac\pi{n}}{\cos\tfrac\pi{n}} \right)^2
,
\end{align}$پس شعاع مشترک برای همه n دایره ها$\begin{align}
r_n&=\tfrac12\,(R-r)
=\frac{r\,\sin\tfrac\pi{n}}{1-\sin\tfrac\pi{n}}
.
\end{align}$
یک مارپیچ ایجاد میکنه که در آن فاصله بین قوس ها رشد میکنه کوچک میشه و به تدریج به توان φ میرسه در هر مضرب $π$ (هر 180 درجه).

من میخوام معادلات پارامتری را برای یک مارپیچ پیدا کنم که در آن این فاصله با توان φ دقیقاً به همان صورت نسبت به مضرب زاویه طلایی، یعنی$\frac{2π}{φ}$ رشد میکنه کوچک میشه
(به جای انجام این کار نسبت به $π$و. φ به صورت $φ=\left(\frac{1+5^{1/2}}{2}\right)$ تعریف میکنم
اگر من مختصات قطبی را در نظر بگیرم $(r,\theta)=(f(t),t)$ با شرط اولیه که منحنی از آن عبور کند$(x,y)=(b,0)$سپس رابطه تعیین کننده منحنیه $f(k\omega) - f(k\omega-2\pi) = \phi^{k+c} = \exp_\phi(k+c) \qquad\qquad f(0) = b\tag{roham1}$جایی که$\omega := 2\pi/\phi$،$k$ یک عدد صحیحه و c فقط برای اطمینان از مضرب ω وجود داره مطابقت با توانهای مناسب ϕ. پیوسته k
$f(t)-f(t-2\pi) = \exp_\phi\left(\frac{t}{\omega}+c\right) \qquad\qquad f(0)=b \tag{roham2}$
فرض کن راه حل دارای فرم$f(t) = a\left(\phi^{t/\omega}-1\right) + b \tag{roham3}$سپس (2roham) نیاز داره$\exp_\phi\left(\frac{t}{\omega}+c\right) = a\exp_\phi\left(\frac{t}{\omega}\right) - a\exp_\phi\left(\frac{t}{\omega}-\frac{2\pi}{\omega}\right)
= a\exp_\phi\left(\frac{t}{\omega}\right) - a\exp_\phi\left(\frac{t}{\omega}-\phi\right) \tag{roham4}$تقسیم سمت چپ ترین و راست ترین عبارات بر$\phi^{t/\omega}$
$\phi^c = a - a\phi^{-\phi} \qquad\to\qquad a = \frac{\phi^{\phi+c}}{\phi^\phi-1}\tag{5}$
به طوری که (3roham) تبدیل میشه$f(t) = \frac{\phi^{\phi+c}}{\phi^\phi-1}\left(\phi^{t/\omega}-1\right) + b \tag{$\star$}$
یک شکل گل را ببینw=9;axis([-w,w,-w,w,-1,1])
L=-w:0.1:w;
f=@(z)(min(1./abs(z).^(2),1));
[X,Y]=meshgrid(L);
Z=X+i*Y;
U=zeros(length(L));
r1=3.4;w1=1.8;
r2=4.5;w2=-0.88;
z1=r1*exp(i*2*a*(0:4));
z2=r2*exp(i*a*(1:2:9));
plot(z1,'*r');plot(z2,'*b');
for k=1:5
U=U+w1*f(Z-z1(k))+w2*f(Z-z2(k));
end;
contour(X,Y,U,3, 'k')
$\begin{align*}
x(t) &= \bigl(1.75 + \cos(5t))\cos\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr), \\
y(t) &= \bigl(1.75 + \cos(5t))\sin\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr),
\end{align*}$
$\begin{align*}
x(t) &= \bigl(1.75 + \cos(5t))\cos\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr), \\
y(t) &= \bigl(1.75 + \cos(5t))\sin\bigl(t + \tfrac{\pi}{20}\sin(10t)\bigr),
\end{align*}$

در هندسه زنجیره اشتاینر مجموعهای از n دایره است که همگی بر دو دایره غیر متقاطع مماس هستن آبی و قرمز که در آن n محدوده و هر دایره در زنجیره مماس بر دایره قبلی است.اگر حداقل یک زنجیره بسته اشتاینر از n دایره برای دو دایره مفروض α و β وجود داشته باشه آنگاه تعداد نامتناهی زنجیره اشتاینر بسته از n دایره وجود داره و هر دایره ای مماس بر α و β به همان شکل عضوی از چنین زنجیره ایه
ساده ترین نوع زنجیره اشتاینر خوب یک زنجیره بسته از n دایره با اندازه مساوی است که یک دایره محاطی به شعاع r را احاطه کرده . زنجیر دایرهها بهخودی خود توسط دایرهای به شعاع R احاطه شده دایرههای محاط شده و محصور شده متحدالمرکز هستن و دایرههای زنجیره اشتاینر در حلقۀ بین آنها قرار دارن با تقارن، زاویه 2θ بین مراکز دایره های زنجیره اشتاینر 360 درجه بر n . چون که دایره های زنجیره اشتاینر بر یکدیگر مماس هستن فاصله بین مراکز آنها برابره با مجموع شعاعشون در اینجا دو برابر شعاع ρ آنها. نیمساز دو مثلث قائم الزاویه با زاویه مرکزی θ = 180 درجه / n ایجاد میکنه سینوس این زاویه را می توان به عنوان طول قطعه مقابل آن تقسیم بر هپوتنوز مثلث قائم الزاویه نوشت.$\sin \theta ={\frac {\rho }{r+\rho }}$و$\rho ={\frac {r\sin \theta }{1-\sin \theta }}$نقاط مماس یک دایره زنجیره ای اشتاینر با دایره های داده شده درونی و بیرونی روی خطی قرار دارن که از مرکز مشترک آنها می گذره. لذا شعاع بیرونی R = r + 2ρ.یک زنجیره بسته اشتاینر از n دایره باید که نسبت شعاع R/r دایره های داده شده دقیقاً برابر باشه شما نسبت عدد طلایی بزار${\frac {R}{r}}=1+{\frac {2\sin \theta }{1-\sin \theta }}={\frac {1+\sin \theta }{1-\sin \theta }}=\left[\sec \theta +\tan \theta \right]^{{2}}$برای دایره های متحدالمرکز این فاصله به عنوان لگاریتم نسبت شعاع آنها تعریف بکنید$\delta =\ln {\frac {R}{r}}$پس $\delta =2\ln \left(\sec \theta +\tan \theta \right).$اگر یک زنجیره اشتاینر حلقوی چندحلقه ای n دایره کل داشته باشه و قبل از بسته شدن به دور m بار بپیچد زاویه بین دایره های زنجیره اشتاینر برابره$∘\theta ={\frac {m}{n}}180^{{\circ }}$

با پایتون یک گل رسم کردم

برنامه
from PIL import Image, ImageDraw
import numpy as np
import matplotlib.pyplot as plt
def draw_fractal(s, ls):
# Create a new image with a white background
image = Image.new('RGBA', (s, s), color = (0, 0, 0, 0))
draw = ImageDraw.Draw(image)
# Begin the recursion
draw_fractal_recursive(draw, s/2, s/2, s/2, 0, ls, s)
# Display the image
plt.imshow(np.array(image))
plt.show()
def draw_fractal_recursive(draw, x, y, o, depth, ls, s):
if depth >= len(ls):
return
# Chain order to corresponding order in input list
n = ls[depth]
# Calculate inner base circle radius
i = (o-o*np.sin(np.pi/n))/(np.sin(np.pi/n)+1)
# Fill based on depth
rgba_color = (0, 0, 0, int(255 * np.power(depth/len(ls), 4)))
# Draw circle
draw.ellipse((x-o, y-o, x+o, y+o), fill=rgba_color)
# Recurse on inner circle
draw_fractal_recursive(draw, x, y, i, depth+1, ls, s)
# Loop through all circles of the chain
for r in range(n):
# Translate origin to middle of the 2 base circles
new_x = x + (o+i)/2 * np.cos(2 * np.pi * r / n)
new_y = y + (o+i)/2 * np.sin(2 * np.pi * r / n)
# Recurse on chain circle
draw_fractal_recursive(draw, new_x, new_y, (o-i)/2, depth+1, ls, s)
# Call the function
draw_fractal(600,[13,7,11,5,3])
من یک دایره C1 با قطر مشخص d1 دارم. آن دایره توسط N دایره (C2) با قطر مجهول d2 احاطه شده که در آن هر یک از دایره های C2 دو دایره C2 همسایه و دایره C1 را در یک نقطه مماسند من حالا. باید d2 را پیدا کنم$\cos\left(\frac{360}{N}\right)= \frac{2(r_1+r_2)^2 -(2r_2)^2}{2(r_1+r_2)^2}$.

که به راحتی با هندسه پایه قابل حله این یک مورد خاص از زنجیره n استاینرهدو دایره با شعاع r<R داده میشه وفاصله بین مراکز آنها d در زنجیره اشتاینر از n دایره ها پارامترهای ذکر شده باید با این معادله مطابقت داشته خوب
$\begin{align}
d^2&=(R-r)^2-4Rr\tan^2\tfrac\pi{n}
\tag{roham hesami1}\label{1}
.\end{align}$برای مورد خاص داده شده،هم شعاع دایره داخلی r و فاصله d=0بنابراین، شعاع R دایره بیرونی را میتونم $\begin{align}
R&=r\cdot\left(\frac{1+\sin\tfrac\pi{n}}{\cos\tfrac\pi{n}} \right)^2
,
\end{align}$پس شعاع مشترک برای همه n دایره ها$\begin{align}
r_n&=\tfrac12\,(R-r)
=\frac{r\,\sin\tfrac\pi{n}}{1-\sin\tfrac\pi{n}}
.
\end{align}$


